2017 清北济南考前刷题Day 1 afternoon

期望得分：80+30+70=180

实际得分：10+30+70=110

T1 水题(water)

Time Limit:1000ms   Memory Limit:128MB

题目描述

LYK出了道水题。

这个水题是这样的：有两副牌，每副牌都有n张。

对于第一副牌的每张牌长和宽分别是xi和yi。对于第二副牌的每张牌长和宽分别是aj和bj。第一副牌的第i张牌能覆盖第二副牌的第j张牌当且仅当xi>=aj并且yi>=bj。（注意牌不能翻转）当然一张牌只能去覆盖最多一张牌，而不能覆盖好多张。

LYK想让两副牌的各n张一一对应叠起来。它想知道第二副牌最多有几张能被第一副牌所覆盖。

输入格式(water.in)

    第一行一个数n。

    接下来n行，每行两个数xi,yi。

    接下来n行，每行两个数aj,bj。

输出格式(water.out)

输出一个数表示答案。

输入样例

3

2 3

5 7

6 8

4 1

2 5

3 4

输出样例

2

数据范围

对于50%的数据n<=10。

对于80%的数据n<=1000。

对于100%的数据1<=n<=100000，1<=xi,yi,aj,bj<=10^9。

对所有的牌按长从小到大排序，x相同时，第二副牌位置靠前

然后枚举所有的牌

如果是第二副牌，就把它的宽 扔到某个数据结构里

如果是第一副牌，就在这个数据结构里找<=它的宽的最大的，数据结构里把它删去，ans++

数据结构如果是数组，n^2,可得80

数据结构用权值线段树、平衡树、multiset 可得100

#include<set>
#include<cstdio>
#include<algorithm>

using namespace std;

#define N 100001

struct node
{
    int x,y,ty;
}e[N<<1];

multiset<int>s;

multiset<int>::iterator it;

bool cmp(node p,node q)
{
    if(p.x!=q.x) return p.x<q.x;
    return p.ty>q.ty; 
}

int main()
{
    freopen("water.in","r",stdin);
    freopen("water.out","w",stdout);
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d%d",&e[i].x,&e[i].y),e[i].ty=1;
    for(int i=1;i<=n;i++) scanf("%d%d",&e[i+n].x,&e[i+n].y),e[i+n].ty=2;
    sort(e+1,e+n*2+1,cmp);
    n<<=1; int ans=0;
    for(int i=1;i<=n;i++)
        if(e[i].ty==2) s.insert(e[i].y);
        else 
        {
            if(s.empty()) continue;
            it=s.upper_bound(e[i].y);
            if(it==s.begin()) continue;
            it--;
            ans++; 
            s.erase(it);
        }
    printf("%d",ans);
} 

T2 梦境(dream)

Time Limit:1000ms   Memory Limit:128MB

题目描述

LYK做了一个梦。

这个梦是这样的，LYK是一个财主，有一个仆人在为LYK打工。

不幸的是，又到了月末，到了给仆人发工资的时间。但这个仆人很奇怪，它可能想要至少x块钱，并且当LYK凑不出恰好x块钱时，它不会找零钱给LYK。

LYK知道这个x一定是1~n之间的正整数。当然抠门的LYK只想付给它的仆人恰好x块钱。但LYK只有若干的金币，每个金币都价值一定数量的钱（注意任意两枚金币所代表的钱一定是不同的，且这个钱的个数一定是正整数）。LYK想带最少的金币，使得对于任意x，都能恰好拼出这么多钱。并且LYK想知道有多少携带金币的方案总数。

具体可以看样例。

输入格式(dream.in)

    第一行一个数n，如题意所示。

输出格式(dream.out)

输出两个数，第一个数表示LYK至少携带的金币个数，第二数表示方案总数。

输入样例

6

输出样例

3 2

样例解释

LYK需要至少带3枚金币，有两种方案，分别是{1,2,3}，{1,2,4}来恰好得到任意的1~n之间的x。

输入样例2

10

输出样例2

4 8

数据范围

对于30%的数据n<=10。

对于60%的数据n<=100。

对于100%的数据n<=1000。

最少金币数=log2（n）下取整 +1

方案数:

dp[i][j][k] 拿了i个金币，当前和为j，最大的是k的方案数

枚举 下一枚金币 h，h∈[k+1,j+1]   dp[i+1][j+h][h]+=dp[i][j][k]

#include<cmath>
#include<cstdio>
#include<algorithm>

#define N 1001

int dp[12][N][N];

int main()
{
    freopen("dream.in","r",stdin);
    freopen("dream.out","w",stdout);
    int n;
    scanf("%d",&n);
    int x=log(n)/log(2)+1;
    dp[1][1][1]=1;
    for(int i=1;i<x;i++)
        for(int j=1;j<=n;j++)
            for(int k=1;k<=n;k++)
                if(dp[i][j][k])
                {
                    for(int h=k+1;h<=j+1;h++)
                        dp[i+1][std::min(j+h,n)][h]+=dp[i][j][k];
                }
    int ans=0;
    for(int i=1;i<=n;i++) ans+=dp[x][n][i];
    printf("%d %d",x,ans);
}

 

T3 动态规划(dp)

Time Limit:1000ms   Memory Limit:128MB

题目描述

LYK在学习dp，有一天它看到了一道关于dp的题目。

这个题目是这个样子的：一开始有n个数，一段区间的价值为这段区间相同的数的对数。我们想把这n个数切成恰好k段区间。之后这n个数的价值为这k段区间的价值和。我们想让最终这n个数的价值和尽可能少。

例如6个数1,1,2,2,3,3要切成3段，一个好方法是切成[1],[1,2],[2,3,3]，这样只有第三个区间有1的价值。因此这6个数的价值为1。

LYK并不会做，丢给了你。

输入格式(dp.in)

    第一行两个数n,k。

    接下来一行n个数ai表示这n个数。

输出格式(dp.out)

一个数表示答案。

输入样例

10 2

1 2 1 2 1 2 1 2 1 2

输出样例

8

数据范围

对于30%的数据n<=10。

对于60%的数据n<=1000。

对于100%的数据1<=n<=100000,1<=k<=min(n,20),1<=ai<=n。

其中有30%的数据满足ai完全相同均匀分布在所有数据中。

n^2 做法：

预处理 f[i][j] 表示[l,r]的价值

dp[i][j] 表示前i个数分为j段的最小价值

状态转移：dp[i][j]=min(dp[k][j-1]+f[k+1][i])

 

优化：

当j固定时，k具有单调性

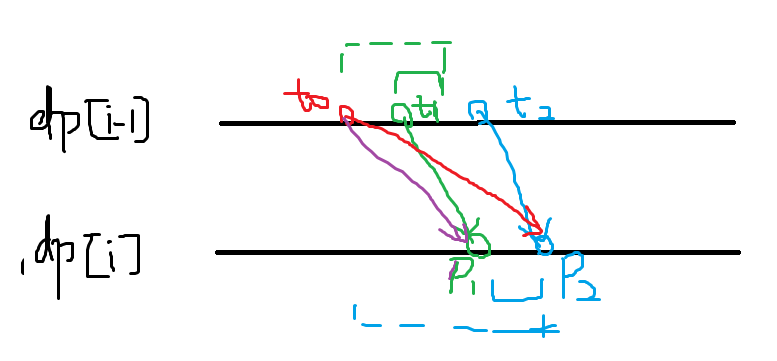
即 若p1由t1（绿色）转移，那么p2只能由t1及之后的t2（蓝色）转移

若p2 由t0（红色） 转移，那么可以证明p1由t0（紫色）转移更优

大概思路就是

由t2转移就是那段短的蓝色区间，由t0转移，蓝色区间延长，它延长就更容易产生价值

这样都更小的话，上面那个绿色的段区间延长也会更小

 

所以，如果确定了dp[mid][i] 由 dp[pos][i-1]转移

那么dp[1][i]~dp[mid-1][i]只能由 dp[1][i-1]~dp[pos][i-1]转移

dp[mid+1][i]~dp[n][i]只能由 dp[pos][i-1]~dp[n][i-1] 转移

这就可以分治下去

 

分治每一层都是n个点，所以时间复杂度为k*n*logn

#include<cstdio>
#include<cstring>

using namespace std;

typedef long long LL;

#define N 100001

LL tot;

int a[N];

int cnt[N],L,R;

LL f[N],g[N];

void move(int l,int r)
{
    while(L>l) --L,tot+=cnt[a[L]],cnt[a[L]]++;
    while(L<l) cnt[a[L]]--,tot-=cnt[a[L]],L++;
    while(R>r) cnt[a[R]]--,tot-=cnt[a[R]],R--;
    while(R<r) ++R,tot+=cnt[a[R]],cnt[a[R]]++;
}

void work(int l,int r,int opl,int opr)
{
    if(opl>opr) return;
    int mid=opl+opr>>1;
    LL mi=1e18; int pos;
    for(int i=l;i<=r;i++)
    if(i<mid)
    {
        move(i+1,mid);
        if(tot+f[i]<mi) mi=tot+f[i],pos=i;
    }
    g[mid]=mi;
    work(l,pos,opl,mid-1);
    work(pos,r,mid+1,opr);
}

int main()
{
    freopen("dp.in","r",stdin);
    freopen("dp.out","w",stdout);
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    f[0]=0;
    for(int i=1;i<=n;i++) f[i]=1e18;
    while(k--)
    {
        memset(cnt,0,sizeof(cnt));
        tot=0; L=1; R=0;
        work(0,n-1,1,n);
        for(int i=1;i<=n;i++) f[i]=g[i],g[i]=0;
    }
    printf("%d",f[n]);
}

70分暴力

#include<cstdio>
#include<cstring>
#include<iostream>

using namespace std;

#define N 1001

int n,k;

int f[N][N],dp[N][N];

int a[N],sum[N];

void read(int &x)
{
    x=0; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); }
}

void pre()
{
    for(int i=1;i<n;i++)
    {
        sum[a[i]]++;
        for(int j=i+1;j<=n;j++)
        {
            f[i][j]=f[i][j-1]+sum[a[j]];
            sum[a[j]]++;
        }
        memset(sum,0,sizeof(sum));
    }
}

void solve()
{
    memset(dp,63,sizeof(dp));
    for(int i=0;i<=n;i++) dp[i][0]=0;
    for(int i=1;i<=n;i++)
    {
        dp[i][1]=f[1][i];
        for(int j=2;j<=min(k,i);j++)
            for(int h=0;h<i;h++)
                dp[i][j]=min(dp[i][j],dp[h][j-1]+f[h+1][i]);
    }
    printf("%d",dp[n][k]);
}

int main()
{
    freopen("dp.in","r",stdin);
    freopen("dp.out","w",stdout);
    read(n); read(k);
    if(n>1000)
    {
        printf("%I64d",1LL*n%k*(n/k)*(n/k+1)/2+1LL*(k-n%k)*(n/k)*(n/k-1)/2);
        return 0;
    }
    for(int i=1;i<=n;i++) read(a[i]);
    pre();
    solve();
    return 0;
}