转载请注明来源
最小生成树简单的来说就是从无向连通图的邻接表或者邻接矩阵中扣下来一棵权值最小的树,他只有n-1条边来连接n个顶点,并且不允许产生回路。
Kruskal算法首先要对边进行排序,sort一遍升序即可。然后要进行的就是抠树啦。最开始的时候把n个点看成独立的n棵树,然后按权值从小到大选择边,所选的边连接的两个顶点u,v应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。 重复直到所有顶点都在一颗树内或者有n-1条边为止。
求最小生成树要用到之前学过的并查集
参考:https://blog.csdn.net/luoshixian099/article/details/51908175
下面贴上代码
#include <bits/stdc++.h> #define fi first #define se second #define pb push_back #define fio ios::sync_with_stdio(false);cin.tie(0); #define pii pair<int,int> #define vi vector<int> #define vc vector<char> #define pi 3.1415926 #define ls l,m,rt<<1 #define rs m+1,r,rt<<1|1 const int INF=0x3f3f3f3f; const int N=2e5+5; typedef long long ll; typedef double db; typedef unsigned long long ull; using namespace std; int n,m; int pre[N]; struct edge { int start; int to; int value; }edges[N]; void InitPre()//初始化pre数组 { for (int i=1;i<=n;i++) { pre[i]=i; } } int findRoot(int n)//查找根节点 { int r=n; while(pre[r]!=r)//查找这个点的根节点 { r=pre[r]; } //r现在是根节点 int i=n,j; while(i!=r)//路径压缩,让小弟直接归老大直辖 { j=pre[i]; pre[i]=r; i=j; } return r; } void join(int x,int y)//把各个连同分支连起来 { int r1=findRoot(x); int r2=findRoot(y); if(r1!=r2)//如果已经连通不用管 { pre[r1]=r2;//不连通的时候随便指定一个是另一个的老大 } } bool cmp(edge a,edge b) { return a.value<=b.value; } void kruskal() { int sumValue=0;//生成树的权值 int cnt=0;//已用边的数量 int start,to,value; for (int i=1;i<=m;i++) { start=edges[i].start; to=edges[i].to; if(findRoot(start)!=findRoot(to)) { cout<<start<<"---"<<to<<" "<<edges[i].value<<endl; sumValue+=edges[i].value; cnt++; join(start,to); } if(cnt>=n-1) break; } cout<<"SumValue: "<<sumValue<<endl; } int main() { //n个点m条边 cin>>n>>m; InitPre(); for (int i=1;i<=m;i++) { cin>>edges[i].start>>edges[i].to>>edges[i].value; } sort(edges+1,edges+1+m,cmp); cout<<endl<<endl; kruskal(); }
测试数据
7 9 1 2 28 1 6 10 2 3 16 2 7 14 3 4 12 4 5 22 4 7 18 5 6 25 5 7 24
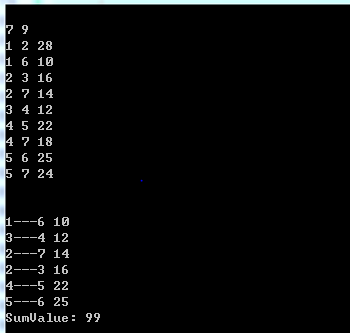
--------------------------------------------------------------------
更新一波,这个板子在一些数据下面会T掉,可能某些方面写的不好。。
重新贴一个
1 #include <bits/stdc++.h> 2 #define fi first 3 #define se second 4 #define pb push_back 5 #define fio ios::sync_with_stdio(false);cin.tie(0); 6 #define pii pair<int,int> 7 #define vi vector<int> 8 #define vc vector<char> 9 #define pi 3.1415926 10 #define ls l,m,rt<<1 11 #define rs m+1,r,rt<<1|1 12 13 const int INF=0x3f3f3f3f; 14 const int N=2e5+5; 15 16 typedef long long ll; 17 typedef double db; 18 typedef unsigned long long ull; 19 using namespace std; 20 struct Edge 21 { 22 int u,v,w; 23 }edge[200005]; 24 25 int fa[5005],n,m,ans,eu,ev,cnt; 26 inline bool cmp(Edge a,Edge b) 27 { 28 return a.w<b.w; 29 }//快排的依据 30 inline int findRoot(int x){ 31 while(x!=fa[x]) x=fa[x]=fa[fa[x]]; 32 return x; 33 } 34 inline void kruskal(){ 35 sort(edge,edge+m,cmp);//将边的权值排序 36 for(int i=0;i<m;i++){ 37 eu=find(edge[i].u), ev=find(edge[i].v); 38 if(eu==ev) continue;//若出现环,则continue 39 ans+=edge[i].w;//更新答案 40 fa[ev]=eu; cnt++; 41 if(cnt==n-1) break;//循环结束条件 42 } 43 } 44 int main(){ 45 scanf("%d%d",&n,&m); 46 for(int i=1;i<=n;i++) fa[i]=i;//初始化并查集 47 for(int i=0;i<m;i++) 48 scanf("%d%d%d",&edge[i].u,&edge[i].v,&edge[i].w); 49 kruskal(); 50 printf("%d",ans); 51 return 0; 52 }