Floyd再思考
——by ThinkofBlank
一.序言
Floyd,是一个十分常用的图论算法,其作用是在O(n^3)的时间内计算出全源最短路。其实现原理是利用的dp,然而,刚开始接触Floyd的时候,并没有去尝试理解,思考此算法,仅仅记了下打法就跑了,最近无聊时思考了下,得出了些有用的东西,特此来分享
注意:以下说的图都是无负环的,不然,求甚么最短路。。。
当然,给出的图是联通且点的个数至少为3
二.引入
1、路径合成可行性
给定一个图,假设我们已知i->j的最短路径为a1,i->k的最短路径为a2,(a1<a2),那么j->k的最短路径是多少?
答案是a2-a1?不!并不是,比如下图:
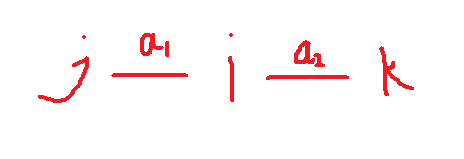
很明显的,j->k的最短路径应该是a1+a2才对,当然,也有满足最短路径为a1-a2的情况,如下图:

所以,如果我们单纯地知道i->j和i->k的最短路径,我们是无法求出正确的j->k的最短路径的
那么,我们来换一换,假设我们已知i->k的最短路径为a1,k->j的最短路径为a2,那么i->j的最短路径是不是就可求呢?
初步画个图:
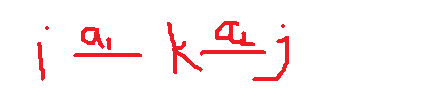
由此可以判断出i->j的最短路径是a1+a2,于是就又错啦!
以下给出两个hack的情况:
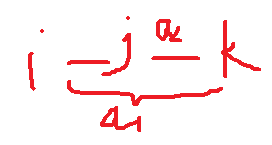
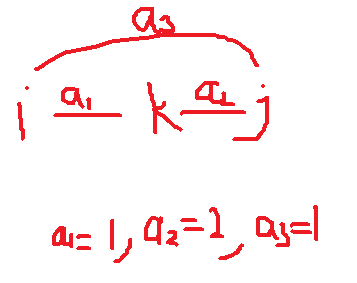
当然,对于第一个hack的情况,要j和k之间的是双相边
于是,我们真的无法求出来了吗?不!
我们注意到,对于两种hack的情况,其实它都可以看出i->k,k->j的行走方式,只是某些时候,k=i或j罢了!
所以,就有:对于一条路径i->j,它可以由i->k,k->j合成,那么我们只需要合成就好了。这就是路径的合成可行性
感性的理解:由i到j,我们可以先从i到k,再从k到j,如果直接由i到j中途不停留的话,那么相当于此时k=i或者j
那么,这里就有一个方法了!
我们枚举所有的k!这样,我们就可以枚举出所有的路径出来!然后把这些权值取最小,即一定为最小路径!
首先,我们设dis(i,j)表示i->j的最短路径(初始无限大),那么如果有一条边权为w从i->j的边,我们就令dis(i,j)=min(dis(i,j),w)
这样我们就求出了对于所有i->k,k->j中k=i或j的时候的路径了
那么之后怎么求呢?
简单啊!
枚举k嘛,我就老老实实枚举k和i,j就好了嘛
for:i=1->n
for:j=1->n
for:k=1->n
dis(i,j)=min(dis(i,j),dis(i,k)+dis(k,j))
看,这不就好了嘛!
然而,这是错的。。。
为啥?
因为我们回过去看枚举所有k得到最短路径的条件:dis(i,k)与dis(k,j)一定也是最短路径!
但是,我们目前,我们对于部分dis(i,k)和dis(k,j)并没有枚举,所以,我们的答案不一定正确!
那么该如何改进呢?
传统的Floyd是使用松弛操作进行的:
for:k=1->n
for:i=1->n
for:j=1->n
dis(i,j)=min(dis(i,j),dis(i,k)+dis(k,j))
咋看一下没啥不同,但事实上,它是在进行dp,具体的我就不说多了,现在来讨论下Floyd的Ex算法:
先来引入一个定理:
2、一定存在两个点最短路径为它们两个点的直接连边
先者有言:没有证明的理论,都是猜想,不能直接用
那么,我们就来证明一波
我使用的是反证法:
假设所有点两两之间的最短路都间隔了至少经过了一个点
我们设i->j的最短路为i->k->j
那么,不难发现,如果i->k的最短路不是i,k的直接连边,而是i->t->k的话,那么明显有i->j的最短路中
i->t->k->j更优
那么i->j的最短路不止经过一点呢,我们直接假设为i->t->k->j,我们可以同理去分析i->t
所以,这与假设不相符
所以,命题得证。
而且,同理去分析k->j,还会再多得一对点,所以对于任意一对最短路为直接连边的两点A,B
我们一定可以找到另外的一个点C,使得那个点与两点中的其中一个点(假设为B)的直接连边是最小路径
简单分析下便可发现,这样的点对至少有n-1个
那么,如果我们找到所有这样的点对,我们就可以再推出至少n-2条最短路径,然后再用这n-2条路径继续推...
循环n-1次便可以推完所有的最短路径了!
三、算法
那,我们怎么找到这n-1条边呢?对于一个图,我们可以采用玄学的方法——枚举法!
这样,我们就有了一个算法的雏形:
一开始的赋值就不说了。。。
首先,我们将所有边加入对应的表中(使用数组即可~),比如u->v,我们就令s(u,++siz(u))=v,表示,我们有一条从
u->v的确定了权值的边(不一定最小)
然后,我们进行一下操作:
1.枚举i
2.访问与i相连的边,找到一个k
3.访问与k相连的边,找到一个j
4.如果dis(i,k)+dis(k,j)<dis(i,j),我们令dis(i,j)=dis(i,k)+dis(k,j),并把j加入i的表中
5.回到步骤1,重复n-2次即可(第一次是赋值那里)
两个优化:
1.对于每个点来说,我们维护一个bool数组ys(i,j)表示j是否在i的表里面,如果是,我们就无需把j加入表中,否则,我们就将j加入表中,并使ys(i,j)=1
2.对于不在起作用的表,我们将它砍掉,无需再访问(详细见代码的kil数组)
于是我们有了代码:
//#pragma GCC optimize()//手动Ox优化
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int M=1001;
int dis[M][M];
int s[M][M],siz[M];
bool kil[M][M];
bool ys[M][M];
inline void Ex_Floyd(int n){
int tim=n-2;
while(tim--){
bool flag=0;
for(int i=1;i<=n;++i){
for(int j=1;j<=siz[i];++j){
int v=s[i][j];
if(kil[i][j]){
continue;
}
kil[i][j]=1;
for(int k=1;k<=siz[v];++k){
int e=s[v][k];
if(dis[i][e]>dis[i][v]+dis[v][e]){
dis[i][e]=dis[i][v]+dis[v][e];
if(!ys[i][e]){
ys[i][e]=1;
s[i][++siz[i]]=e;
}
flag=1;
kil[i][j]=0;
}
}
}
}
if(!flag){
break;
}
}
}
signed main(){
int n,m;
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
dis[i][j]=1e16;
}
dis[i][i]=0;
}
for(int i=1;i<=m;++i){
int u,v,w;
scanf("%lld%lld%lld",&u,&v,&w);
if(dis[u][v]>w){
if(!ys[u][v]){
ys[u][v]=1;
s[u][++siz[u]]=v;
}
dis[u][v]=w;
}
}
Ex_Floyd(n);
return 0;
}
我们把它称作Ex_Floyd算法,为什么呢?我们通过一道题来说明:
http://ybt.ssoier.cn:8088/problem_show.php?pid=1421
我们惊奇的发现,传统的Floyd算法竟然无法通过此题,而此算法可以
经过尝试发现,Floyd错的点中,存在负权边
事实证明,传统的Floyd似乎不能跑负权边啊。。。
而此算法可以,故命名为Ex_Floyd(经过一番尝试后,发现,此算法应与Floyd的复杂度接近,不过常数可能会大点)