权值线段树、可持久化线段树 以及 主席树 基础

权值线段树与第Kth 大/小

可持久化线段树解决历史信息记录问题

权值线段树+可持久化 = 静态主席树

权值线段树:

权值线段树和常用的线段树区别在于，基础线段树维护(sum,min,max,xor)等值，而权值中结点位置表示的是该结点的值所对应的个数，从而维护区间的个数。由于题中给出的数不是连续的，有可能差值很大，所以我们要先进行离散化处理，然后再构造该数据结构。

在查询总的第(Kth)时，我们可以通过判断当前(k)与右节点个数来寻找位置。如果小于等于右节点维护的区间中值出现的次数，则向右走，否则减去右节点的权值次数然后向左走，这样就能查询到区间(1)到(n)的第(Kth).

那我要求某个区间的第(Kth)大怎么搞？

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+5;
struct node
{
	int num;
}seg[maxn<<1];
void push_up(int p){
	seg[p].num = seg[p<<1].num + seg[p<<1|1].num;
}
void build(int l,int r,int p){
	if(l==r){
		//优先往左然后往右保证一次增大
		scanf("%d",&seg[p].num);
		return ;
	}
	int mid = l+r>>1;
	build(l,mid,p<<1);
	build(mid+1,r,p<<1|1);
	push_up(p);
}
//递归查询:总的第k大 
int query(int k,int l,int r,int p){
	int mid = l+r>>1;
	if(l==r){
		return l;
	}
	if(k<=seg[p<<1|1].num) return query(k,mid+1,r,p<<1|1);
	else return query(k-seg[p<<1|1].num,l,mid,p<<1);
}
int main(){
	int n;
	cin>>n;
	build(1,n,1);
	int m;
	cin>>m;
	for(int i=1;i<=m;i++){
		int k; cin>>k;
		cout<<"k:"<<query(k,1,n,1)<<endl;
	}
}

上面的代码便是基于“传统”的线段树，建堆的方式搭的一棵树。左右结点直接通过 (p<<1)和(p<<1|1) 既可以得到，既可以直接通过下标的倍增操作得到左右结点。

要能够查询某个区间的第K大，我们还要保留历史信息，即使之成为可持久化的线段树，加入动态开点操作。

动态开点，即 增加对某个结点左右儿子的记录 ，例如加入(lc,rcspace(leftspace child,rightspace child))信息

这样我要寻找其左右儿子是通过 (seg[rt].lc) 或者 (seg[rt].rc) 得到 , 而不是 (seg[rt<<1]) 或者 (seg[rt<<1|1])

关于每一个结点存的位置，我们可以直接顺序存放在数组中即可。用一个(cnt)来记录存放在数组的第几个位置即可

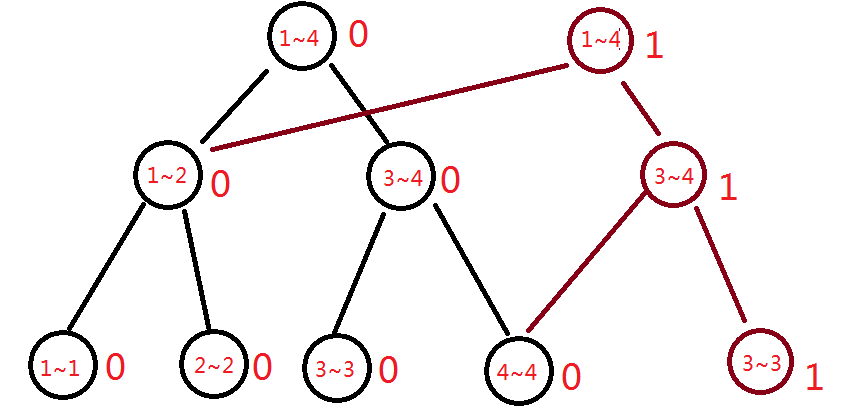
我们知道在更新一个点时，其所有祖先结点都要更新一边。如果树深为(n),则最多新增(log^n)个结点，同时所有的点都会将根结点进行更新。所以我们用一个(root)数组代表每一次修改后的新增加结点链的根。

例如下图，我们在更新4~4区间时，则会新增红色部分的链

可持久化线段树 例题：洛谷P3919

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,m,a[N],root[N];
int cnt=0,lc[N<<6],rc[N<<6],val[N<<6];
//动态建树函数 一般都会返回新建结点编号 
int build(int l,int r) {
    int q=++cnt;  //动态建树 
    if (l==r) {
        lc[q]=rc[q]=0; val[q]=a[l];
        return q;
    }
    int mid=l+r>>1;
    lc[q]=build(l,mid);
    rc[q]=build(mid+1,r);
    return q;
}

//这个其实是插入函数，因为公用结点的缘故并不能修改版本信息导致其他版本受影响 
int update(int p,int l,int r,int x,int v) {  //新版本线段树是基于版本p而来 
    int q=++cnt;  //动态建树
    if (l==r) {
        lc[q]=rc[q]=0; val[q]=v;
        return q;
    } 
    int mid=l+r>>1;
    lc[q]=lc[p]; rc[q]=rc[p]; val[q]=val[p];  //为了公用信息，先复制一份 
    if (x<=mid) lc[q]=update(lc[p],l,mid,x,v);
    if (x>mid) rc[q]=update(rc[p],mid+1,r,x,v);
    return q;  
}

int query(int p,int l,int r,int x) {  //查询版本p位置x的值 
    if (l==r) return val[p];
    int mid=l+r>>1;
    if (x<=mid) return query(lc[p],l,mid,x);
    if (x>mid) return query(rc[p],mid+1,r,x); 
}

int main()
{
    cin>>n>>m;
    for (int i=1;i<=n;i++) scanf("%d",&a[i]);
    root[0]=build(1,n);
    
    for (int i=1;i<=m;i++) {
        int k,opt,x,v; scanf("%d%d",&k,&opt);
        if (opt==1) {
            scanf("%d%d",&x,&v);
            root[i]=update(root[k],1,n,x,v);
        } else {
            scanf("%d",&x);
            printf("%d
",query(root[k],1,n,x));
            root[i]=root[k];
        }
    }
    return 0;
}

主席树静态查询区间第K大 例题：洛谷P3834

通过之间可持久化线段树对历史操作状态的记录，然后类似前缀和的思想，查询区间([L,R])的第(K)大，即是查询从(L到R)次操作新增部分中的第(K)大。

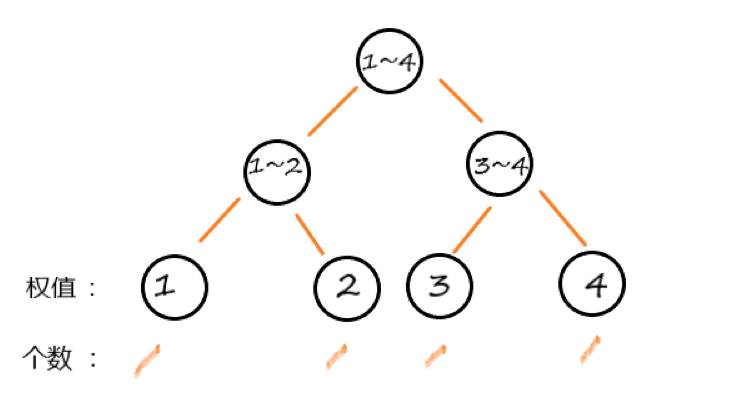
如下图：一开始比如在第(4)次插入权值之后，为下面这一棵权值线段树。

在第8次插入权值后，为下图状态

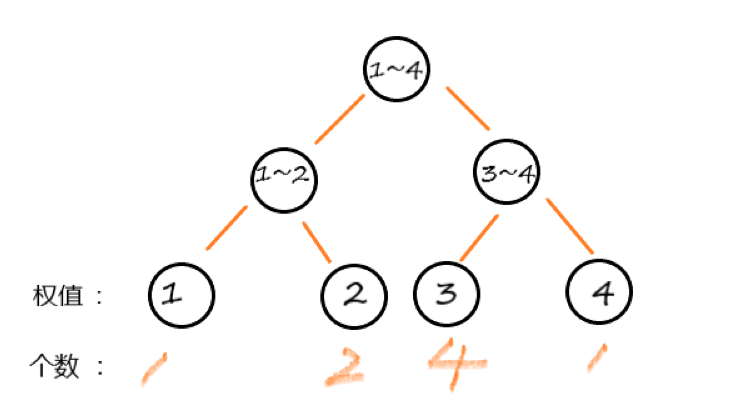
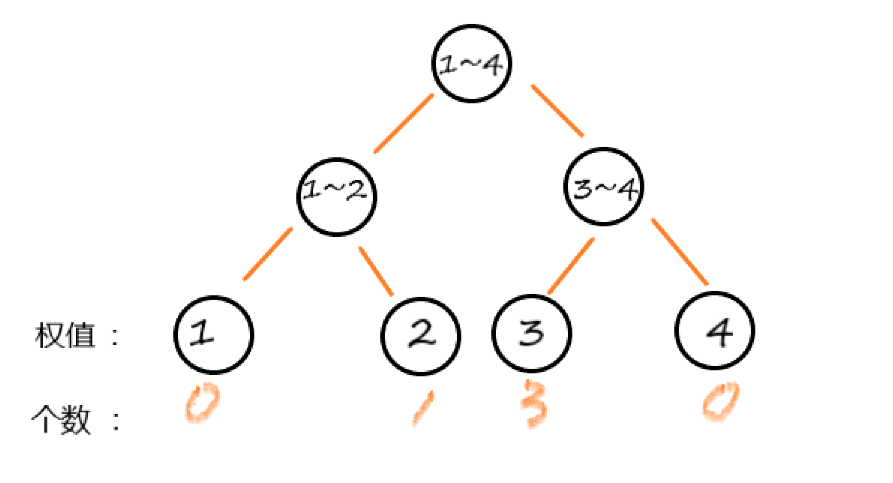
也就是说，在([4,8])的操作区间中，新增加了(1个2)，和(3个4) （这里的2，4表示离散化之后对应的原数组的第(2th)和第(4th))

假如一开始n个数的序列为： 1 2 3 4 2 4 4 4 ，那么实际上查询([4,8])范围也就是查询新加入的部分 ({2,4,4,4})的第(Kth) ，而要得到新增加的有哪些部分，则可以用当前信息(第8次操作后)的权值线段树的值减去之前（第4次操作后的值），那么这时候我们查询这个([4,8])区间内的第K大，不就可以用当时权值线段树查询的方式去找了么？

Code:

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(0); cin.tie(0);
using namespace std;
const int maxn = 1e6+5;
int cnt;
int root[maxn];
struct node{
    int val,lc,rc;
}seg[maxn<<6];
int a[maxn],b[maxn];
int build(int l,int r){
	int p = ++cnt;
	if(l==r){
		seg[p].val = 0;
		seg[p].lc = seg[p].rc = 0;
		return p;
	}
	int mid = l+r>>1;
	seg[p].lc  = build(l,mid);
	seg[p].rc  = build(mid+1,r);
	return p;
}
void push_up(int p){
	seg[p].val = seg[seg[p].lc].val + seg[seg[p].rc].val; //维护区间信息
}
int update(int q,int l,int r,int k){
	int p = ++cnt;
	if(l==r){
		seg[p].val = seg[q].val + 1;
		seg[p].lc = seg[p].rc = 0;
		return p;
	}
	seg[p] = seg[q]; //赋值结点值
	int mid =l+r>>1;
	if(k<=mid) seg[p].lc = update(seg[q].lc,l,mid,k);
	if(k>mid) seg[p].rc = update(seg[q].rc,mid+1,r,k);
	push_up(p);
	return p;
}
int query(int l,int r,int L,int R,int k){
	if(l==r) return b[l];
	int mid = l+r>>1;
	int num = seg[seg[R].lc].val - seg[seg[L].lc].val;
	if(k<=num) return query(l,mid,seg[L].lc,seg[R].lc,k);
	if(k>num) return query(mid+1,r,seg[L].rc,seg[R].rc,k-num); 
}
int main(){
	IOS
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i],b[i] = a[i];
	sort(b+1,b+1+n);
	int tot = unique(b+1,b+1+n) - (b+1);
	cnt = 0; root[0] = build(1,n);//建空树
	for(int i=1;i<=n;i++){
		int x = lower_bound(b+1,b+1+tot,a[i]) - b;//最小为1
		root[i] = update(root[i-1],1,tot,x);
	}
	for(int i=1;i<=m;i++){
		int L,R,k;
		cin>>L>>R>>k;
		cout<<query(1,tot,root[L-1],root[R],k)<<endl;
	}
	return 0;
}