


那么这一道题我在考试的时候写挂了(0分 呜呜~)
我原来的思路是广搜来骗取部分分(哈哈~)
但是我忘记了一个非常重要的问题
我广搜开的数组没有考虑负的下标
下一次考试如果再写暴力
就可以把坐标都加上一个数就行了~
那么这一道题 n<=10^6 每一个点的坐标在 ±10^18次方之间
那么这个数据范围就很尴尬了
广搜深搜。。。都肯定不行!
那么应该咋办呢??
我们来想一下
假如要从 (sx,sy) 走到 (ex,ey)
移动分为被动和主动
其实只要主动走的方向和被动走的方向是正好相反的
那么醉汉就待在原地不动了
也就是说
假如醉汉到家的最短时间是t
那么t+1他也同样能到家
t+2 t+3 t+4....只要醉汉想待下去,就可以一直待在原地
我们来看一个数轴
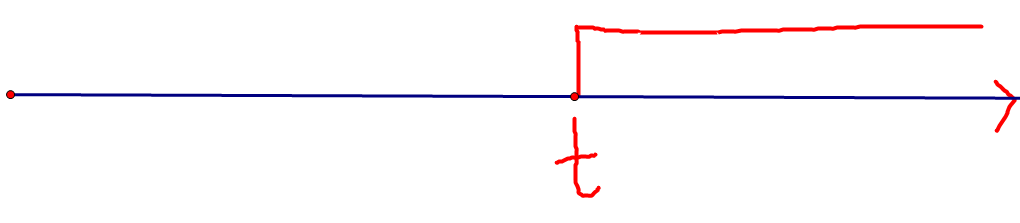
t往右的都可以往左的则不行
这就满足了可二分性
可以进行二分答案
10^18 二分也就最多30次
当然不超时咯,很快就会出答案
那么每一个时间怎么来判断它是不是成立呢
首先从起点到终点我们可以算一个曼哈顿距离
然后醉汉的移动是有周期的
比如SSZX
那么一个周期下来相当于向上移动了一格,向左移动了一格
t/n的就可以直接计算出来
t%n的就直接模拟一下就行了
二分答案在确定当前枚举的步数t是否成立时,可以先把原坐标被动移动后的新坐标求出来 然后再求曼哈顿距离,判断是否小于等于t
加油~
/* 那么这一道题我在考试的时候写挂了(0分 呜呜~) 我原来的思路是广搜来骗取部分分(哈哈~) 但是我忘记了一个非常重要的问题 我广搜开的数组没有考虑负的下标 下一次考试如果再写暴力 就可以把坐标都加上一个数就行了~ 那么这一道题 n<=10^6 每一个点的坐标在 ±10^18次方之间 那么这个数据范围就很尴尬了 广搜深搜。。。都肯定不行! 那么应该咋办呢?? 我们来想一下 假如要从 (sx,sy) 走到 (ex,ey) 移动分为被动和主动 其实只要主动走的方向和被动走的方向是正好相反的 那么醉汉就待在原地不动了 也就是说 假如醉汉到家的最短时间是t 那么t+1他也同样能到家 t+2 t+3 t+4....只要醉汉想待下去,就可以一直待在原地 我们来看一个数轴 t往右的都可以往左的则不行 这就满足了可二分性 可以进行二分答案 10^18 二分也就最多30次 当然不超时咯,很快就会出答案 那么每一个时间怎么来判断它是不是成立呢 首先从起点到终点我们可以算一个曼哈顿距离 然后醉汉的移动是有周期的 比如SSZX 那么一个周期下来相当于向上移动了一格,向左移动了一格 t/n的就可以直接计算出来 t%n的就直接模拟一下就行了 二分答案在确定当前枚举的步数t是否成立时,可以先把原坐标被动移动后的新坐标求出来 然后再求曼哈顿距离,判断是否小于t 加油~ */ #include<bits/stdc++.h> using namespace std; string s; int Movx,Movy; long long sx,sy,ex,ey; int n; int check(long long t){ long long ans=0; long long X=sx,Y=sy; X+=Movx*(t/n); Y+=Movy*(t/n); long long movx=0,movy=0; int Left=t%n; for(int i=0;i<Left;i++){ if(s[i]=='S') movy++; if(s[i]=='X') movy--; if(s[i]=='Z') movx--; if(s[i]=='Y') movx++; } X+=movx; Y+=movy; ans+=abs(ex-X); ans+=abs(ey-Y); if(ans<=t) return 1; return 0; } void Turning(){ for(int i=0;i<n;i++){ if(s[i]=='S') Movy++; if(s[i]=='X') Movy--; if(s[i]=='Z') Movx--; if(s[i]=='Y') Movx++; } } int main() { freopen("drunk.in","r",stdin); freopen("drunk.out","w",stdout); cin>>n; cin>>s; cin>>sx>>sy>>ex>>ey; Turning(); long long l=0,r=4100000000000000000; int flag=0; // cout<<check(9); long long ans=0; while(l<=r){ long long mid=(l+r)/2; // cout<<l<<" "<<r<<" "<<mid<<endl; if(check(mid)==1){ flag=1; ans=mid; r=mid-1; } else l=mid+1; } if(flag==0){ cout<<"Impossible"; return 0; } cout<<ans; return 0; }