数据结构-队列

 

 

 

 

一、  队列的定义

1. 1.        为什么要学习队列？

你们在用电脑时有没有经历，机器有时会处于疑似死机的状态，鼠标点什么似乎都没用，双击任何快捷方式都不动弹。就当你失去耐心，打算rest时。突然他像酒醒了一样，把你刚才点击的所有操作全部按顺序执行一遍。这其实是因为操作系统中的多个程序因需要通过一个通道输出，而按先后次序排队等待造成的。

再比如向移动、联通、电信等客服电话，客服人员与客户相比总是少数，在所有的客服人员都占线的情况下，客户会被要求等待，直到有某个客户人员空下来，才能让最先等待的客户接通电话。这里也是将所有当前打客服电话的客户进行排队处理。

操作系统和客服系统中，都是应用了一种数据结构来实现刚才提到的先进先出的排队功能，这就是队列。

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

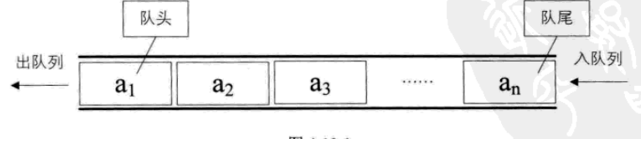
队列是一种先进先出（First in First Out）的线性表，简称FIFO。允许插入的一端称为队尾，允许删除的一端称为队头。假设队列是q=（a1,a2,…,an），那么a1就是队头元素，而an是队尾元素。这样我们就可以删除时，总是从a1开始，而插入时，列在最后。这也比较符合我们通常生活中的习惯，排在第一个的优先出列，最后来的当然在队伍的最后。

队列在设计程序中用的非常频繁。比如用键盘进行各种字母或数字的输入，到显示器如记事本软件上的输出，其实就是对列的典型应用，假如你本来和女友聊天，想表达你是我的上帝，输入的是god，而屏幕上却显示出了dog发了出去，这真是要气死人了

一、  队列的抽象数据类型

同样是线性表，队列也有类似线性表的各种操作，不同的就是插入数据只能在队尾进行，删除数据只能在队头进行。

一、   ACM算法：队列的实现

队列的定义：

#include "stdio.h"

#define MAXSIZE  5    //最大容量是5个元素

struct queue   //队列

{

       int a[MAXSIZE];   //队列元素

       int front;          //队头

       int rear;           //队尾

};

1. 1.        入队操作

算法：

              步骤一：判断是否溢出，若溢出给出提示结束程序，否则跳到步骤二

        步骤二：输入入队的元素

        步骤三：将元素存于队尾处

        步骤四：队尾下标自增

//入队操作

void enqueue(struct queue *q)

{

       int e;

       if(q->rear<MAXSIZE-1)

       {

              printf("请输入入队的元素：");

           scanf("%d",&e);

              q->a[q->rear]=e;

              q->rear++;

              printf("入队成功 ");

       }

       else

       {

              printf("溢出 ");                                   

       }

}

1. 2.        出队操作

算法：

              步骤一：判断是有元素，若无元素则给出提示结束程序，否则跳到步骤二

        步骤二：用e接收出队的元素

        步骤三：

        步骤四：队尾下标自增

//出队操作

void dequeue(struct queue *q)

{

       int e;

       if(q->front==q->rear)

       {

              printf("队空，没有元素 ");

       }

       else

       {          

              e=q->a[q->front];

           q->front++;

           printf("出队的元素是%d ",e);                    

       }

}    

二、       循环队列

所以解决假溢出的办法就是后面满了，就再从头开始，也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。

刚才的例子继续，把它的rear可以改为指向下标为0的位置，这样就不会造成指针指向不明的问题了。

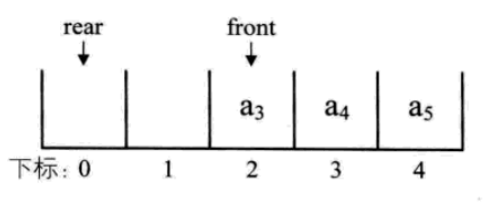
接着入队a6，将它放置于下标为0处，rear指针指向下标为1处，若再入队a7，则rear指针就与front指针重合，同时指向下标为2的位置。

此时问题又出来了，我们刚才说，空入队列时，front等于rear，现在当队列满时，也是front等于rear，那么如何判断此时的队列究竟是空还是满呢？

办法一是设置一个标致变量flag，当front==rear，且flag=0时时为队列空，当front==rear，且flag=1时为队列满。

办法二是当队列空时没条件就是front=rear，当队列满时，我们修改其条件，保留一个元素空间。也就是说，队

我们重点来讨论第二种方法，由于rear可能比front大，也可能比front小，所以尽管他们只相差一个位置是就是满的情况，但也可能是相差整整一圈，所以若队列的最大尺寸为QueueSize，那么队列满的条件是（rear+1）%QueueSize==front（取模“%”的目的就是为了整合rear与front大小为一个问题）。比如上面这个例子，QueueSize=5中的front=0，而rear=4，（4+1）%5=0，所以此时队列满。再比如front=2而rear=1.（1+1）%5=2，所以此时队列也是满的。而对于front=2和rear=0，（0+1）%5=1，1≠2，所以此时队列并没有满。

另外，当rear>front时，此时队列的长度为rear—front.但当rear<front时，队列长度分为两端，一端是QueueSize—front,另一端是0+rear，加在一起，队列长度为rear—front+QueueSize.因此通用的计算机队列队列长度公式为：

（rear—front+QueueSize）%QueueSize

有了这些讲解，现在实现循环队列的代码就不难了。循环队列的顺序存储结构代码如下：

#include "stdio.h"
#include "stdlib.h"
#define MAX 6
struct stack{
    int a[MAX];
    int rear;
    int font;
    }s;
void main()
{
    int bh;
    int e,i;
    s.rear=0;
    s.font=0;
    printf("
1.入队
2.出对
3.打印
4.退出
");
    for(;;){
        scanf("%d",&bh); 
        switch(bh){
            case 1:
            if((s.rear+1)%MAX==s.font){
                printf("溢出
");
                break;
            }else{
                printf("输入入队数据:");
                scanf("%d",&e);
                s.a[s.rear]=e;/* 人为浪费一个空间 */
                s.rear=(s.rear+1)%MAX;//尾部加一
                
            }
            break;
            case 2:
            if(s.rear==s.font){
                printf("队列为空！
");
                break;
            }else{
               e=s.a[s.font];
               s.font=(s.font+1)%MAX;
               printf("出队的元素是%d
",e);
            }
            break;
            case 3:
            if(s.rear==s.font){
                printf("队列为空！
");
                break;
                }
            if(s.rear>s.font){
                for(i=s.font;i<s.rear;i++){
                    printf("%d  ",s.a[i]);
                    }
            }else{
/*                for(i=s.font;i<MAX;i++){
                    printf("%d  ",s.a[i]);
                }
                for(i=0;i<s.rear;i++){
                    printf("%d  ",s.a[i]);
                    }*/
                    for(i=s.font;i!=s.rear;i=(i+1)%MAX){
                        printf("%d  ",s.a[i]);
                        }//两个都可以用这个
            }
            break;
            case 0:
            exit(0);
            break;
            default :
            printf("输入功能编号有误！
");
            
            }
        }
}

循环队列plus版本

/* Note:Your choice is C IDE */
#include "stdio.h"
#define MAX 20
struct student
{
    int age[MAX];
    int top;//记录头节点
    int rear;//记录尾节点
};
void add(struct student *s)
{
    int a;
    printf("请输入您要添加的数字
");
    scanf("%d",&a);
    if(s->rear<MAX)
    {
        s->age[s->rear]=a;
        if(s->rear>MAX)
        {
            s->rear=0;        
        }else{
            s->rear++;
        }
        }
    
}
void delete(struct student *s)
{
    if(s->rear==s->top)
    {
        printf("**没有元素**
");
    }else{
        if(s->top>MAX)
        {
            s->top=0;
        }else{
            s->top++;
        }
    }
}
void menu()
{
    printf("********************
");
    printf("**进队**************
");
    printf("**出队**************
");
    printf("**显示队列**********
");
    printf("********************
");
    }
void main()
{
    struct student s;
    int bh,i;
    s.rear=0;
    s.top=0;
    menu();
    while(1)
    {
        printf("请输入选项");
        scanf("%d",&bh);
        switch(bh)
        {
            case 1:
                add(&s);
                break;
            case 2:
                delete(&s);
                break;
            case 3:
                for(i=s.top;i!=s.rear;i=(i+1)%MAX){
                    printf("|%d",s.age[i]);
                }
                printf("
");
                break;
            case 0:
                exit(0);
                break;
            default:
                printf("您输入的选项有误！！！
");
                break;
            }
        }
    
}