@description@
JOHNKRAM 最近在研究排序网络,但他发现他不会制作比较器,于是他用交换器来代替比较器。
一个交换器有两个输入端 x, y 和两个输出端 x′, y′。如果交换器处于关闭状态,则 x 收到的信号会从 x′ 发出,y 收到的信号会从 y′ 发出。如果交换器处于开启状态,则 x 收到的信号会从 y′ 发出,y 收到的信号会从 x' 发出。
JOHNKRAM 设计了这样一个递归定义的网络:
(1)1阶网络就是一个交换器。
(2)n (n>1) 阶网络的第一排是 2^(n−1) 个交换器,接下来是两个 n−1 阶网络,最后一排也是2^(n−1) 个交换器。
将第一排的输出端和第二排的输入端分别从左到右标号为 0∼2^n−1,第一排的 i 输出端连接到第二排的 i>>1 输入端,其中 >> 指n位二进制数的循环右移。
类似,将倒数第一排的输入端和倒数第二排的输出端分别从左到右标号为 0∼2^n−1,倒数第二排的 i 输出端连接到倒数第一排的 i<<1 输入端,其中 << 指 n 位二进制数的循环左移。
一个3阶的网络如下图所示:
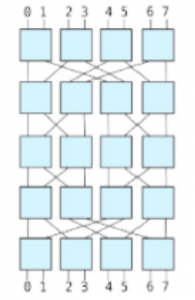
JOHNKRAM 通过开关交换器来调整网络。现在他对一个 n 阶网络的 2^n 个输入端分别输入了一个数,第 i (0≤i<2^n) 个输入端输入的是 i。然后他给出了一个长度为 2^n 的排列 p。他希望你给出一种网络的状态,使得第 i (0≤i<2^n) 个输出端输出的是 pi。
input
包括不超过 10 组数据,每组数据包含两行。
第一行包含一个整数 n,其中 1≤n≤13。
第二行 2^n 个整数表示排列 p。
输入以 0 结尾。
output
如果无解,输出 -1。
否则输出 2n - 1 行,每行包含 2^(n-1) 位的二进制数,表示网络的状态。如果那一位的交换器开启则为 1,否则为 0。
如果有多解,输出字典序最小的解。
每组数据输出之间用空行隔开。
sample input
2
3 2 1 0
3
3 7 4 0 2 6 1 5
0
sample output
00
11
11
0011
0000
0110
1111
1101
@solution@
递归定义的结构可以使用递归求解(要用递归打败递归!)
在 n 阶网络中,不难发现对于第一行的交换器而言,它的左输出端只会连接到左边的 n-1 阶网络,右输出端只会连接到右边的 n-1 阶网络。同理对最后一行的交换器,它的左输入端只会连接到左边的 n-1 阶网络,右输入端只会连接到右边的 n-1 网络。
同时,我们发现如果开启第一行的交换器,只会影响输入端的两个数哪一个进左边的网络,哪一个进右边的网络。最后一行同理。
记 a[i] 表示第一行第 i 个交换器是否打开(打开为 1,否则为 0),b[i] 表示最后一行第 i 个交换器是否打开。
记 c[i] 表示数 i 在第一行哪个交换器输入, d[i] 表示数 i 在最后一行哪个交换器输出。
记 e[i] 表示数 i 在第一行的交换器的左边输入还是右边输入(左边为 0,右边为 1),f[i] 表示数 i 在最后一行的交换器的左边输入还是右边输入。
则如果一个网络合法,对于每一个数 i,一定满足 e[i] xor f[i] xor a[c[i]] xor b[d[i]] = 0。
因为是求字典序最小的解,所以可以在第一行从左到右枚举每一个交换器是 0 还是 1,再通过上面那个式子 bfs 进行合法性判定。
决定好了第一行与最后一行,就可以递归解决两个 n-1 阶的子问题。总时间复杂度 O(2^(2n))。
题目虽然说无解输出 -1,但实际上总是有解,可以通过归纳法证明(虽然我代码还是判了无解的)。
为了实现简单可以总是将第一行的输入端调成 0 1 2 3…… 的形式。
@accepted code@
#include<cstdio>
#include<queue>
using namespace std;
const int MAXN = 13;
int x[1<<MAXN], y[1<<MAXN], tp;
int ans[MAXN<<1][1<<MAXN];
int a[1<<MAXN], n, s, t, u;
int tmp1[1<<MAXN], tmp2[1<<MAXN], tmp3[1<<MAXN], tmp4[1<<MAXN];
int stk3[1<<MAXN], stk4[1<<MAXN], tp3, tp4;
queue<int>que;
void restore() {
while( tp3 ) tmp3[stk3[tp3--]] = -1;
while( tp4 ) tmp4[stk4[tp4--]] = -1;
}
bool check(int x, int y) {
stk3[++tp3] = x, tmp3[x] = y;
que.push(x<<1), que.push(x<<1|1);
while( !que.empty() ) {
int f = que.front(); que.pop();
if( f < (u<<1) ) {
if( tmp4[tmp2[f]>>1] != -1 ) {
if( (tmp3[f>>1] == tmp4[tmp2[f]>>1]) != ((f&1) == (tmp2[f]&1)) ) {
restore();
return false;
}
}
else {
stk4[++tp4] = tmp2[f]>>1;
tmp4[tmp2[f]>>1] = (f&1)^(tmp2[f]&1)^tmp3[f>>1];
que.push((tmp2[f]^1) + (u<<1));
}
}
else {
f -= (u<<1);
if( tmp3[tmp1[f]>>1] != -1 ) {
if( (tmp3[tmp1[f]>>1] == tmp4[f>>1]) != ((f&1) == (tmp1[f]&1)) ) {
restore();
return false;
}
}
else {
stk3[++tp3] = tmp1[f]>>1;
tmp3[tmp1[f]>>1] = (f&1)^(tmp1[f]&1)^tmp4[f>>1];
que.push(tmp1[f]^1);
}
}
}
tp3 = tp4 = 0;
return true;
}
int main() {
freopen("left.in", "r", stdin);
freopen("left.out", "w", stdout);
while( scanf("%d", &n) == 1 && n ) {
s = (1<<n), t = (s>>1);
for(int i=0;i<s;i++)
scanf("%d", &a[i]);
bool flag = true;
for(int i=n;i>=1;i--) {
/*printf("| ");
for(int j=0;j<s;j++)
printf("%d ", a[j]);
puts("");*/
u = (1<<(i-1));
for(int j=0;j<t;j+=u) {
for(int k=0;k<u;k++) {
tmp1[k<<1] = a[(j+k)<<1], tmp1[k<<1|1] = a[(j+k)<<1|1];
tmp2[tmp1[k<<1]] = k<<1, tmp2[tmp1[k<<1|1]] = k<<1|1;
tmp3[k] = tmp4[k] = -1;
}
for(int k=0;k<u;k++) {
if( tmp3[k] == -1 ) {
if( !check(k, 0) && !check(k, 1) ) {
flag = false;
break;
}
}
}
for(int k=0;k<u;k++)
ans[n-i+1][j+k] = tmp3[k], ans[n+i-1][j+k] = tmp4[k];
for(int k=0;k<u;k++) {
if( !tmp4[k] ) a[(j<<1)+k] = (tmp1[k<<1]>>1), a[(j<<1)+k+u] = (tmp1[k<<1|1]>>1);
else a[(j<<1)+k] = (tmp1[k<<1|1]>>1), a[(j<<1)+k+u] = (tmp1[k<<1]>>1);
// printf(". %d %d
", j+k, j+k+u);
/*printf("| ");
for(int j=0;j<s;j++)
printf("%d ", a[j]);
puts("");*/
}
if( !flag ) break;
}
if( !flag ) break;
}
if( !flag ) puts("-1");
else {
for(int i=1;i<=2*n-1;i++) {
for(int j=0;j<t;j++)
printf("%d", ans[i][j]);
puts("");
}
}
puts("");
}
}
@details@
康复计划 - 8。
切水题是真~的~爽~
有一个很烦的细节就是比较器与输入输出端的下标转换。