像水,玻璃,钻石一类的干净的材质都是电解质。当光照射它们的时候,光会分解成反射光线和折射(透射)光线。我们将通过在反射或折射之间随机选择(?)来处理这种情况,并且每次交互只产生一个散射光线。调试最困难的部分是折射光线。 如果有折射光线,我通常首先将所有的光线折射。 对于这个项目,我试图在我们的场景中放两个玻璃球,我得到了这个:

这是对的吗?玻璃球虽然在现实中看起来也怪怪的。但是不,这是不对的。
上下应该颠倒,并且去掉黑色的东西。我只是打印出了直穿图像中心的光线,这显然是错的。
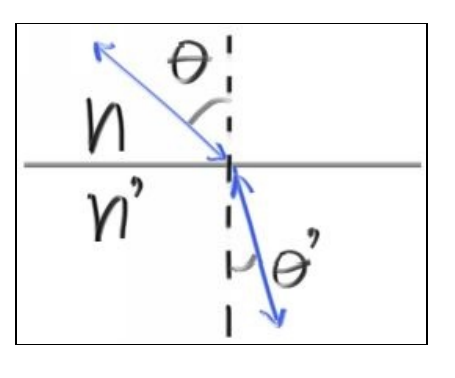
折射由斯涅尔定律(折射定律)定义:
n sin(theta) = n’ sin(theta’)
折射率公式也常表示为
其中n和n'都是折射率(通常空气折射率为1,玻璃为1.3-1.7,钻石为2.4),折射公式画图表示为
1 import math 2 from material import material 3 from metal import metal 4 from rayMath import vec3 5 from ray import ray 6 class dielectric(material): 7 def __init__(self,ri): 8 self.ref_idx=ri 9 def refract(self,v,n,ni_over_nt,refracted): 10 uv=v.unit_vector() 11 dt=uv.dot(n) 12 discriminat=1.0-ni_over_nt*ni_over_nt*(1-dt*dt) 13 if discriminat>0: 14 vec_a=ni_over_nt*(uv-n*dt)-n*math.sqrt(discriminat) 15 refracted.e[0]=vec_a.e[0] 16 refracted.e[1]=vec_a.e[1] 17 refracted.e[2]=vec_a.e[2] 18 return True 19 else: 20 return False 21 def scatter(self,r_in,rec,attenuation,scattered): 22 outward_normal=vec3(0,0,0) 23 reflected=metal.relfect(metal(vec3(0,0,0)),r_in.direction(),rec.normal) 24 attenuation.e[0]=1.0 25 attenuation.e[1]=1.0 26 attenuation.e[2]=1.0 27 ni_over_nt = 0.0 28 refracted=vec3(0,0,0) 29 if r_in.direction().dot(rec.normal)>0: 30 outward_normal= -1*rec.normal 31 ni_over_nt=self.ref_idx 32 else: 33 outward_normal=rec.normal 34 ni_over_nt=1.0/self.ref_idx 35 if self.refract(r_in.direction(),outward_normal,ni_over_nt,refracted): 36 ray_a=ray(rec.p,refracted) 37 scattered.A=ray_a.A 38 scattered.B=ray_a.B 39 else: 40 ray_b=ray(rec.p,reflected) 41 scattered.A=ray_b.A 42 scattered.B=ray_b.B 43 return False 44 return True
一个令人头疼的实际问题是,当光线在折射率较高的材料中时,斯内尔定律没有真正的解决方案,因此不存在折射。在这里所有的光线都会被反射,因为实际上通常在固体物体内部,所以它被称为“全内反射”。这就是为什么当你被淹没时,水 - 空气边界有时会成为完美的镜子。折射代码比反射更复杂一点:
当xx时,介质材料总是折射: