2.5 球形逆映射

　　一旦在球面上找到一个交点和法线，就需要进行进一步的操作。一种常见的阴影技巧是纹理映射，在纹理映射中，球面上交点的位置被用来表示球面的特征。例如，假设要渲染一个地球仪，计算机中存储着一个世界地图。每次球面相交时，在地图上找到合适的颜色，用来给像素着色。

　　问题只是把交点转换成经度和纬度。推导是相当直接的，尽管它涉及一些耗时的三角运算。

　　

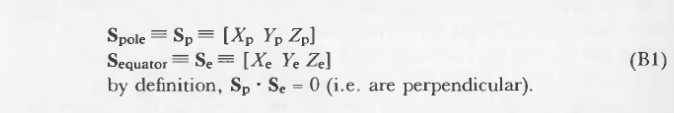
　　S_p是一个单位矢量，它从球体的中心指向球体的北极。S_e是指向赤道上一个参考点的单位矢量。参数u沿赤道从0变化到1。它可以追溯到坐标系统的标准方向(例如，如果使用右手坐标系，那么它在赤道周围的逆时针方向变化)。在极点处，定义u为0。参数v从0到1从南极到北极(技术上说，从-S_p到+ S_p)不等。这个映射如图5所示:

　　

　　交点的法线r_n与由中心和交点形成的单位向量相同。 

　　从这些定义中，首先获得纬度参数。它等于交点法向量和北极的点积的反余弦:

　　

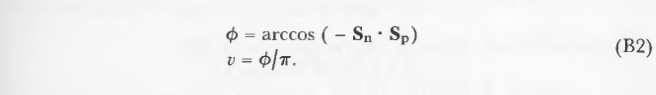
　　注意，要加快代码速度，可以将/ pi的除法转换为乘1/pi。如果v等于0或1，那么u被定义为等于0。否则计算经度参数:

　　1,求坐标和直角坐标的转换关系可以得出P_n   2，1带入S_e点积S_n的代数解： 

　　

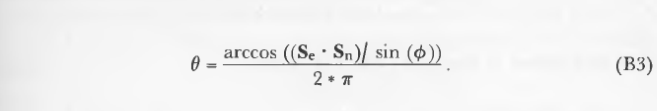
　　现在取两个确定角度的球面轴的外积(叉乘)，并将这个方向与法线的方向进行比较:

　　

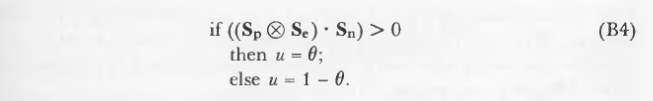
　　注意，叉乘可以预先计算一次。这个测试的作用是确定插入点所在的S_e向量的哪一边。