3.1 光线/平面相交

　　先定义一个光线：

　　　　

　　　　

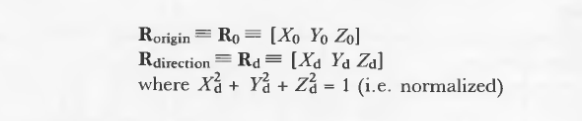
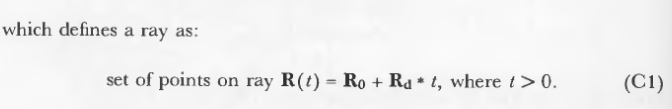
　　虽然不需要对光线方向进行标准化，但是，还是建议进行标准化，否则t将代表长度的距离。　　

　　再定义一个平面：

　　　　

　　　　

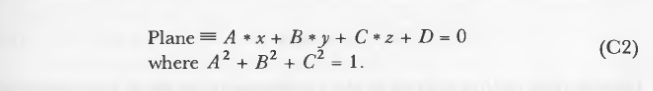
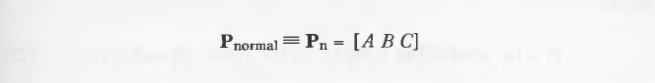
　　然后坐标系统原点到平面的距离是D, D的符号决定了系统原点在平面的哪一边。这是平面的隐式函数。

　　通过将方程(C1)的展开式代入平面方程(C2)，得到射线原点到平面P的交点的距离:

　　　　

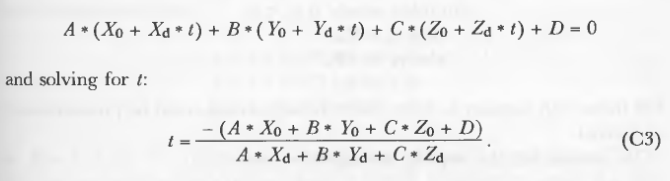
　　以向量表示，点积代数式。方程为：

　　　　

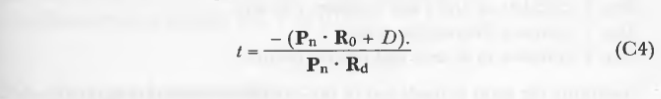
　　为了更有效地使用(C3)，首先计算点积：

　　　　

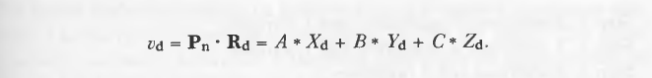
　　如果V_d=0，说明P_n垂直R_d,即光线平行于平面，光线和平面不发生相交。诚然，光线可能位于次平面上，但这种情况是没有意义的;击中多边形边缘对渲染没有影响。同样，如果V_d<0，P_n和R_d的夹角大于90°，这种情况下平面的法线远离光线。如果建模系统使用的是单面平面对象，光线无法透过平面，那么测试将在这里结束，因为平面已经被剔除。如果光线通过这些测试，计算第二个点积。

 　　　　

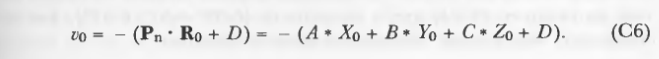
　　现在计算点积的比值:

　　　　

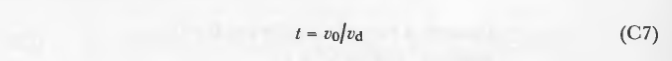
　　如果t<0，在光源后，没有实际的交点。否则，计算交点:

　　　　

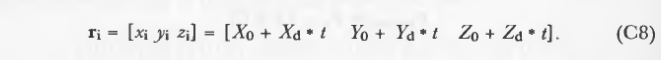
　　通常，需要曲面法向量的是面向光线的法向量，因此可以根据其与方向向量Rd的关系来调整法向量Pn的符号。为了指向射线源，正常的符号应该被反转。（平面双面，所以可选相交面）

　　　　

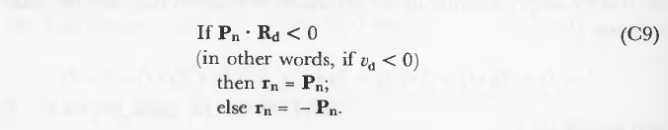
　　对于那些需要烧内存的，可以预先计算并保存反向正常。

　　总结来看，步骤是：

　　　　1，计算V_d然后判断是否为0

　　　　2，计算V₀和t，然后比较t和0

　　　　3，计算交点

　　　　4，计算v0到0和反向法线