续上:SVM中的kernel
带Kernel 的linear regression
kernel可应用到别的算法,不仅仅在SVM
一、常见kernel
l 多项式:二维到三维

l 高斯核函数(需要正规化)



l sigmoid kernel

l cosine similarity kernel

l chi-squared kernel

二、linear regression 曲线

三、带kernel 的PCA
如果我们将m个数据点映射到一个>=m维空间中,就能很容易地构建一个超平面将数据点做任意分类。
PCA定义:

3.1 PCA降维过程
牺牲一部分信息,过滤掉一些干扰(信息压缩,信息的损失最少)
有两个特征值,保留大的(方差最大的方向)
第2步:使得均值在原点,即均值为0

3.2 kernel PCA
实例:

先kernel投影到高维空间,再用PCA降维

线性-->非线性

使用kernel
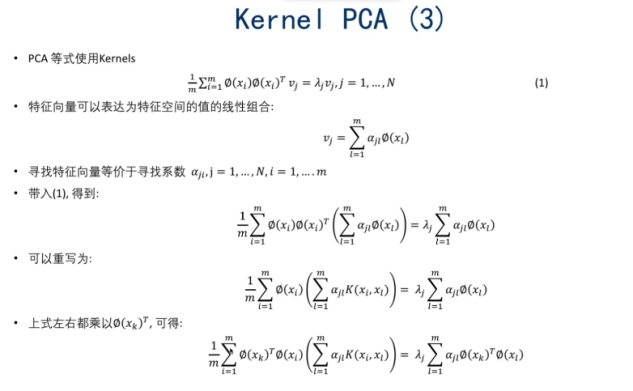

结论:只需要用kernel函数,不用先映射到一个高维空间

PCA后的Kernel和原来的kernel不是同一个kernel
3.3 kernel的选择与参数
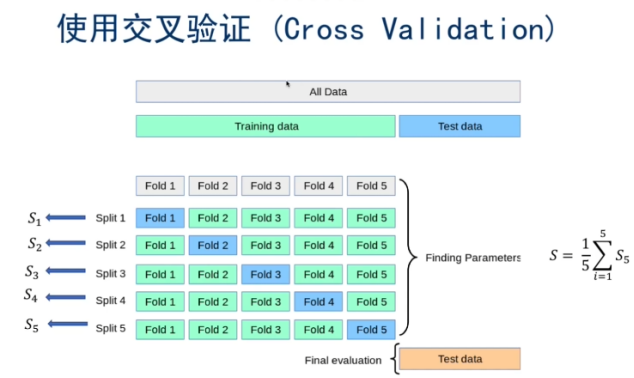
3.3.1 交叉验证(cross validation)
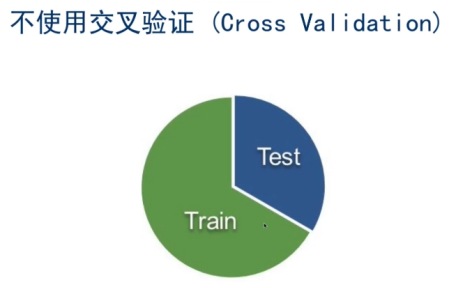
调参:选择validation
|
parameter_candidates = [ {‘C’:[1,10,100,1000],’kernel’:[‘linear’]} {‘C’:[1,10,100,1000],’gamma’:[0.001,0.0001],’kernel’:[‘rbf’]} ] clf = GridSearchCV(estimator = svm.SVC(),param_grid=parameter_candidates,cv = 5,n_jobs = -1) //n_jobs 多线程,=-1用所有的CPU clf.fit(X_train,y_train)
|
3.3.2 VC维
https://www.zhihu.com/question/31727466
为什么用kernel更加容易计算
理论:它反映了模型的学习能力,VC维越大,则模型的容量越大

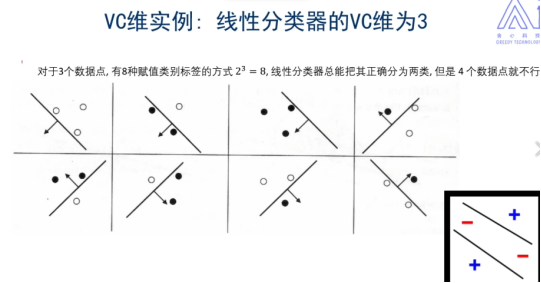
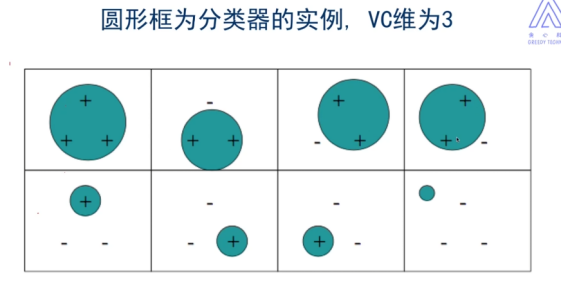
线性分类器:逻辑回归、线性回归、线性SVM