poj 1521

http://poj.org/problem?id=1521

题意：给你一个字符串，首先是计算出一个按正常编码的编码长度，其次是计算出一个用霍夫曼编码的编码长度，最后求正常编码的长度除以霍夫曼编码长度的值，保留一位小数。

思路：正常的编码长度的话，由于都是ASCII码值所以编码长度都为8，所以总长度就是8*字符串的长度Len,然后霍夫曼编码的话，discuss里面很多人都是用优先队列，用优先队列的话，就不用自己维护了，我没用采用优先队列，而是一直维护一个递减的数组，这样的效果和有优先队列是一样的。

霍夫曼编码的示意图

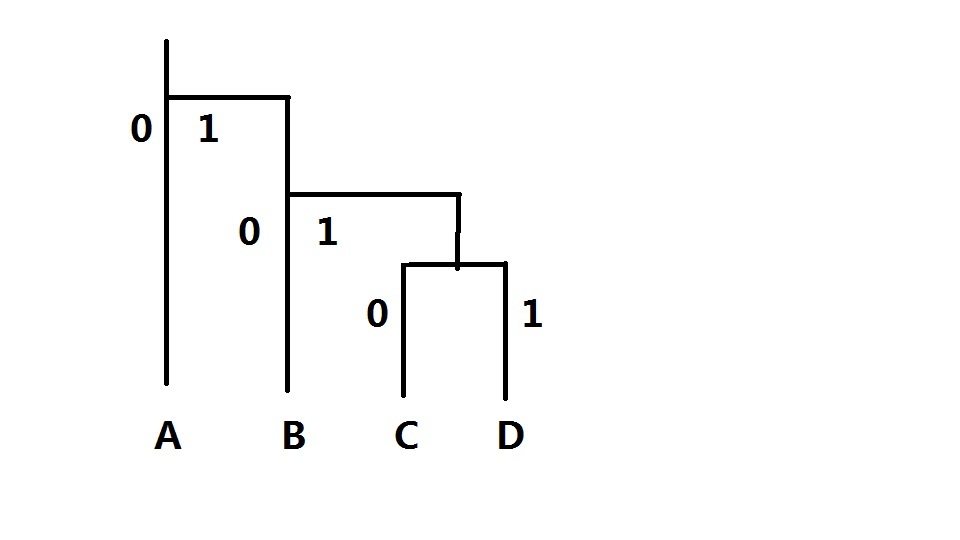
我在这里假设，A有10个，B有5个，C有3个，D有一个。

那么霍夫曼编码的话，就是这样编的。

而这道题是求霍夫曼编码的编码长度。

为什么C和D会比B要多一个编码长度，因为C和D在树枝上要比B要多一个分叉点，那么那个如果没有这个分叉点的话，C和D的编码长度就是和B的一样。

那么我们就可以首先用个把最少的两个字符数加起来，因为在现阶段每个字符都可以看出是只有一个0或者1编码编成的。然后把这两个字符合并起来，意思就是我可以看成没有D这个元素，而是有4个C。

这样就少了一个分叉点，这4个C又和5个B构成了一个分叉点。在现阶段，我们又可以把这5个B和4个C看成只有1个编码长度（0或1）构成的，然后把这两个字符的数加起来，在把这两个字符合并。

相当于只有10个A和9个B构成的。然后A就由0编码，B就由1编码，在把他们两个字符数相加，在合并，最后就相当于有19个A了。然后就编码就结束了。

这里或许有些人会不理解，其实你想，比如说D加了几次。首先D是在和C合并之前就加了一次，然后，D就被C包含了。然后C再和B合并之前有加了一次，这里就相当于D有又加了一次，最后B又包含了C，

最后B在和A合并之前又加了一次，这就可以说明。D是被加了3次的。D的编码长度也就是3，在上面图示上的D的编码也就是111.

每个分叉点的数目都是它下面所有的分支的数目和。而下面的分支在合并之前就加了一次。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

char inp[1000];

int s[200];

int cmp(const void *a,const void *b)
{
    return (*(int *)b)-(*(int *)a);
}

int main()
{
    while(scanf("%s",inp),strcmp(inp,"END")!=0)
    {
        int ans=0;
        memset(s,0,sizeof(s[0]));
        int len=strlen(inp);
        for(int i=0;i<len;i++)
            s[inp[i]]++;
        qsort(s,130,sizeof(s[0]),cmp);
        if(s[0]==len) ans=len;
        else while(s[0]!=len){
            int i=0;
            for(;s[i]!=0;i++);    //这里注意有个分号，目的是找出它的最小的那个点。
                ans+=s[--i];
                ans+=s[i-1];
                s[i-1]+=s[i];
                s[i]=0;
            qsort(s,i,sizeof(s[0]),cmp);   //霍夫曼编码，是从最小的那两个开始编的。
        }
        printf("%d %d %.1f
",len*8,ans,1.0*len*8/ans);
        memset(inp,0,sizeof(inp));
    }
    return 0;
}