https://vjudge.net/problem/Gym-101147B
题意:一个人怕热,他想穿过这条街道,他想要尽可能少的晒到太阳,求最少需要晒多少太阳。
很明显是最短路。只不过问题在于构图。只要把这个图建立出来了,一个dij伙子floyd就可以解决这个问题
构图:
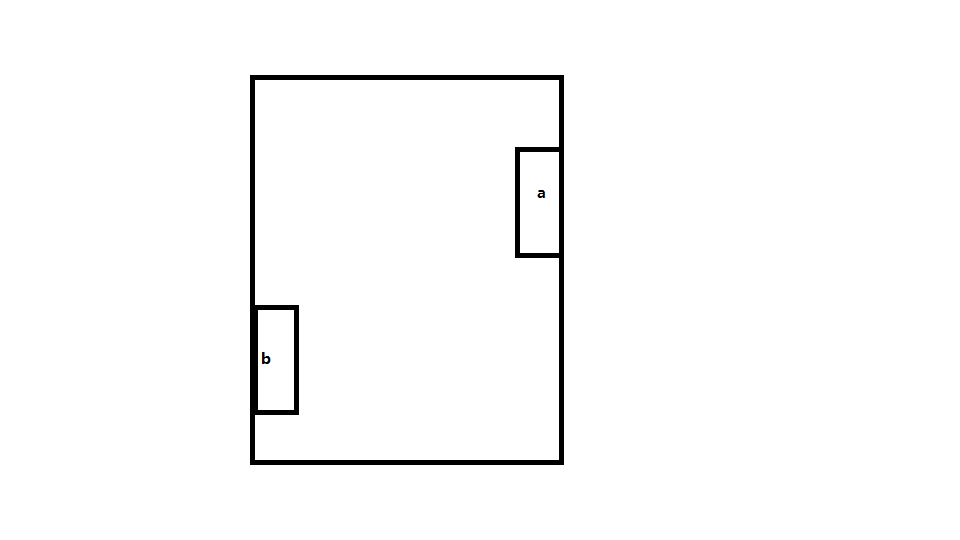
对于这种分布在一边的,两个矩形的距离就等于
两个矩形离起点的距离减去下面矩形的高就可以了
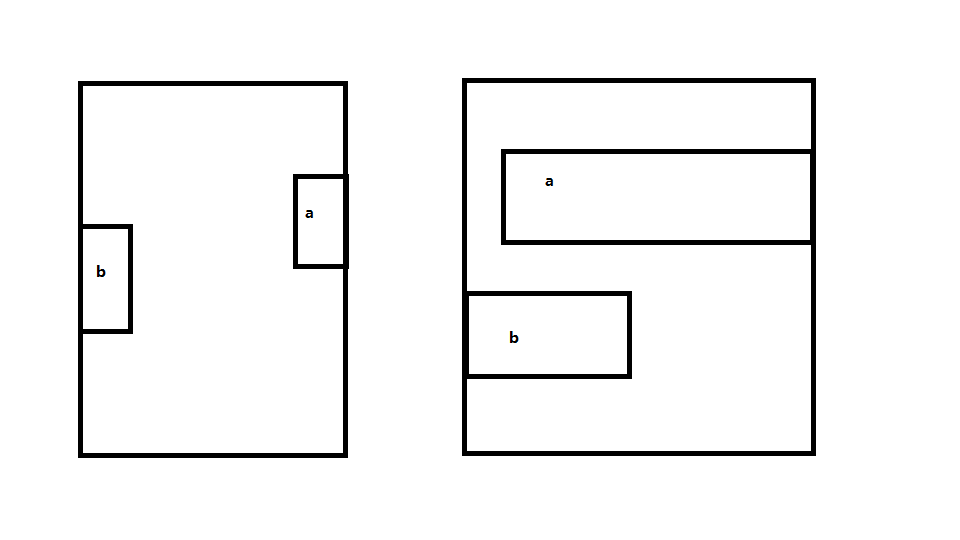
还有的不外乎这几种分布不在一边的,当然也还可以重合,但是重合分在第二种情况考虑
第一种,比较b的右上点和a的左下点的距离和b的左下点和a的右上点的距离,取小的便可
第二种,就是街道的宽度-a和b的宽度与0比较,大于0距离则为wi-a.wi-b.wi,否则说明二者可以重合,距离为0
第三种,则只需要考虑他们之间与起点的距离,大的减去小的便可,第三种不用和0比,因为第三种重合的话,必定为第二中情况
1 #include <stdio.h> 2 #include <string.h> 3 #include <math.h> 4 #include <iostream> 5 #include <stdlib.h> 6 #include <algorithm> 7 #include <queue> 8 #define maxn 111 9 using namespace std; 10 11 double Dis[maxn][maxn]; 12 int n,wi,len; 13 14 15 struct Rect 16 { 17 int k,di,width,len; 18 } rect[105]; 19 20 double dis(Rect a,Rect b) 21 { 22 if(a.k==b.k) 23 { 24 if(a.di>b.di) 25 return a.di-(b.di+b.len)>0?a.di-(b.di+b.len):0; 26 else 27 return b.di-(a.di+a.len)>0?b.di-(a.di+a.len):0; 28 } 29 else if(a.k==1&&b.k==0) 30 { 31 if((a.di+a.len>=b.di&&a.di<=b.di)||(a.di<=b.di+b.len&&a.di>=b.di))//二者有重合部分 32 return wi-a.width-b.width>0?wi-a.width-b.0; 33 else if(wi-a.width-b.width<=0) 34 return a.di-(b.di+b.len)>b.di-a.di-a.len?a.di-(b.di+b.len):b.di-a.di-a.len; 35 return 36 sqrt(1.0*(b.width-wi+a.width)*(b.width-wi+a.width)+1.0*(b.di-a.len-a.di)*(b.di-a.len-a.di))> 37 sqrt(1.0*(b.width-wi+a.width)*(b.width-wi+a.width)+1.0*(b.di+b.len-a.di)*(b.di+b.len-a.di))? 38 sqrt(1.0*(b.width-wi+a.width)*(b.width-wi+a.width)+1.0*(b.di+b.len-a.di)*(b.di+b.len-a.di)): 39 sqrt(1.0*(b.width-wi+a.width)*(b.width-wi+a.width)+1.0*(b.di-a.len-a.di)*(b.di-a.len-a.di)); 40 } 41 else 42 { 43 if((b.di+b.len>=a.di&&b.di<=a.di)||(b.di<=a.di+a.len&&b.di>=a.di))//二者有重合部分 44 return wi-b.width-a.width>0?wi-b.width-a.0; 45 else if(wi-a.width-b.width<=0) 46 return a.di-(b.di+b.len)>b.di-a.di-a.len?a.di-(b.di+b.len):b.di-a.di-a.len; 47 return 48 sqrt(1.0*(a.width-wi+b.width)*(a.width-wi+b.width)+1.0*(a.di+a.len-b.di)*(a.di+a.len-b.di))> 49 sqrt(1.0*(a.width-wi+b.width)*(a.width-wi+b.width)+1.0*(a.di-b.len-b.di)*(a.di-b.len-b.di))? 50 sqrt(1.0*(a.width-wi+b.width)*(a.width-wi+b.width)+1.0*(a.di-b.len-b.di)*(a.di-b.len-b.di)): 51 sqrt(1.0*(a.width-wi+b.width)*(a.width-wi+b.width)+1.0*(a.di+a.len-b.di)*(a.di+a.len-b.di)); 52 } 53 return 0; 54 } 55 56 57 58 int main() 59 { 60 freopen("street.in","r",stdin); 61 // freopen("in.txt","r",stdin); 62 int t; 63 int a,b,c,d; 64 scanf("%d",&t); 65 while(t--) 66 { 67 scanf("%d%d%d",&n,&len,&wi); 68 for(int i = 1; i<=n; i++) 69 { 70 scanf("%d%d%d%d",&rect[i].len,&rect[i].width,&rect[i].di,&rect[i].k); 71 } 72 for(int i = 1;i<=n;i++) 73 { 74 Dis[0][i] = Dis[i][0] = rect[i].di; 75 Dis[n+1][i] = Dis[i][n+1] = len-rect[i].di-rect[i].len; 76 } 77 Dis[0][n+1] = Dis[n+1][0] = len; 78 for(int i = 1;i<=n;i++) 79 { 80 for(int j = 1;j<=n;j++) 81 { 82 Dis[i][j] = dis(rect[i],rect[j]); 83 } 84 } 85 for(int k=0;k<=n+1;k++) 86 for(int i=0;i<=n+1;i++) 87 for(int j=0;j<=n+1;j++) 88 Dis[i][j]=min(Dis[i][j],Dis[i][k]+Dis[k][j]); 89 printf("%.6lf ",Dis[0][n+1]); 90 } 91 return 0; 92 }