梯度下降的问题

%matplotlib inline
import gluonbook as gb
import math
from mxnet import nd
import numpy as np

eta = 0.4

def f_2d(x1,x2):
    return 0.1*x1**2 + 2*x2**2

def gd_2d(x1,x2,s1,s2):
    return (x1-eta*0.2*x1,x2-eta*4*x2,0,0)

def train_2d(trainer):
    x1,x2,s1,s2 = -5,-2,0,0
    results = [(x1,x2)]
    for i in range(20):
        x1,x2,s1,s2 = trainer(x1,x2,s1,s2)
        results.append((x1,x2))
    print('epoch %d,x1 %f,x2 %f' % (i+1,x1,x2))
    return results

def show_trace_2d(f,results):
    gb.plt.plot(*zip(*results),'-o',color='#ff7f0e')
    x1,x2 = np.meshgrid(np.arange(-5.5,1.0,0.1),np.arange(-3.0,1.0,0.1))
    gb.plt.contour(x1,x2,f(x1,x2),colors='#1f77b4')
    gb.plt.xlabel('x1')
    gb.plt.ylabel('x2')

show_trace_2d(f_2d,train_2d(gd_2d))

eta = 0.6
show_trace_2d(f_2d,train_2d(gd_2d))

可以看到，x2 比 x1 的斜率的绝对值更大。

给定学习率，迭代自变量时会使自变量在竖直方向比水平方向移动幅度更大。那么我们需要一个较小的学习率从而避免自变量在竖直方向上越过目标函数最优解。然而，这样又会造成自变量在水平方向上朝着最优解移动变慢。

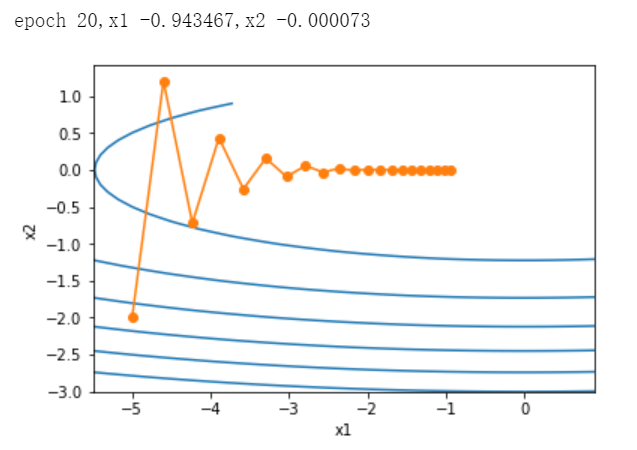
调大学习率，竖直方向的自变量，不断越过最优解，并发散。