无向图的双连通分量

双连通包括两种：　　

　　1、点-双连通： 任意两点之间至少存在两条“点不重复”的路径，即内部无割顶。

　　2、边-双连通： 任意两点之间至少存在两条“边不重复的”路径，即内部无桥。

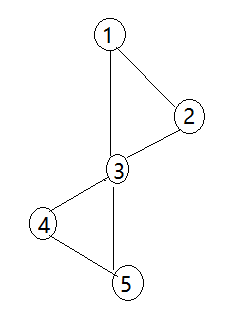
如图：

两个点-双连通分量：{1,2,3}、{3,4,5}；

一个边-双连通分量：{1,2,3,4,5}；

还是利用无向图的割顶和桥的数据结构，和思想。

每次成功找到没有访问的点，边入栈，当发现 子节点v 不能连到 u 的 祖先，那么一个点 - 连通分量找到了。

不断出栈，这些边都是点-连通分量的边。

#include <bits/stdc++.h>
using namespace std;

const int Maxnode = 1000;

int pre[Maxnode<<1];

bool iscut[Maxnode];
int bccno[Maxnode];
int dfs_clock;
int bcc_cnt;

vector<int> G[Maxnode],bcc[Maxnode];

struct Edge
{
    int u,v;
    Edge(int u=0,int v = 0) : u(u),v(v) {}
};

stack<Edge> S;

int dfs(int u,int fa)
{
    int lowu = pre[u] = ++dfs_clock;
    int child = 0;

    for(int i=0; i<G[u].size(); i++)
    {
        int v = G[u][i];
        Edge e = (Edge) { u,v };
        if(!pre[v])
        {
            S.push(e);
            child ++;
            int lowv = dfs(v,u);
            if(lowv>=pre[u])
            {
                iscut[u] = true;
                bcc_cnt ++;
                bcc[bcc_cnt].clear();

                for(;;)
                {
                    Edge x = S.top();
                    S.pop();
                    if(bccno[x.u]!=bcc_cnt)
                    {
                        bcc[bcc_cnt].push_back(x.u);
                        bccno[x.u] = bcc_cnt;
                    }
                    if(bccno[x.v]!=bcc_cnt)
                    {
                        bcc[bcc_cnt].push_back(x.v);
                        bccno[x.v] = bcc_cnt;
                    }
                    if(x.u==u&&x.v==v) break;
                }
            }
        }
        else if(pre[v]<pre[u]&&v!=fa)
        {
            S.push(e);
            lowu = min(lowu,pre[v]);
        }
    }

    if(fa<0&&child==1)
            iscut[u] = 0;
    return lowu;
}

void find_bcc(int n) {

    memset(pre,0,sizeof(pre));
    memset(iscut,0,sizeof(iscut));
    memset(bccno,0,sizeof(bccno));

    dfs_clock = bcc_cnt = 0;

    for(int i=0;i<n;i++) {
        if(!pre[i]) {
            dfs(i,-1);
        }
    }


}