约瑟夫问题

题目链接：http://vjudge.net/contest/143428#problem/A

约瑟夫问题原型： 0~n-1 n 个数，从 0 开始，每数 k 个数，删除一个，最后留下来的数是多少。

题意： 1~n 个数，第一次删掉 m ,每隔 k 个数删掉一个，最后留下来的数是多少。

分析： 

约瑟夫原型： 设从 0 开始 每k 个数删掉一个，最后留下的是 f(n);

则有递推公式 f(n) = （f(n-1) + k）% n;

理由：

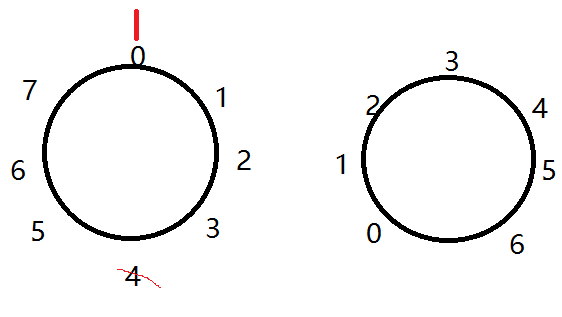
第一次删掉 4 ，那么如果没有了，只可能是旁边的 5 （每次都重新排序了，第二个图）；

那么本题是，1~n ，第一次删掉的是 m，而不像原型里面要数，一上来就删，则起点就是 m+ 1-k，答案 f(n) + m + 1-k;

#include <bits/stdc++.h>
using namespace std;

const int maxn = 10000 + 5;
int f[maxn];


int main()
{
    int n,k,m;
    while(scanf("%d%d%d",&n,&k,&m),n) {
        f[1] = 0;
        for(int i=2;i<=n;i++) {
            f[i] = (f[i-1]+k) % i;
        }

        int ans = (m+1+f[n]-k) % n;
        if(ans<=0) ans+=n;
        printf("%d
",ans);
    }


    return 0;
}