二叉索引树，LA2191，LA5902，LA4329

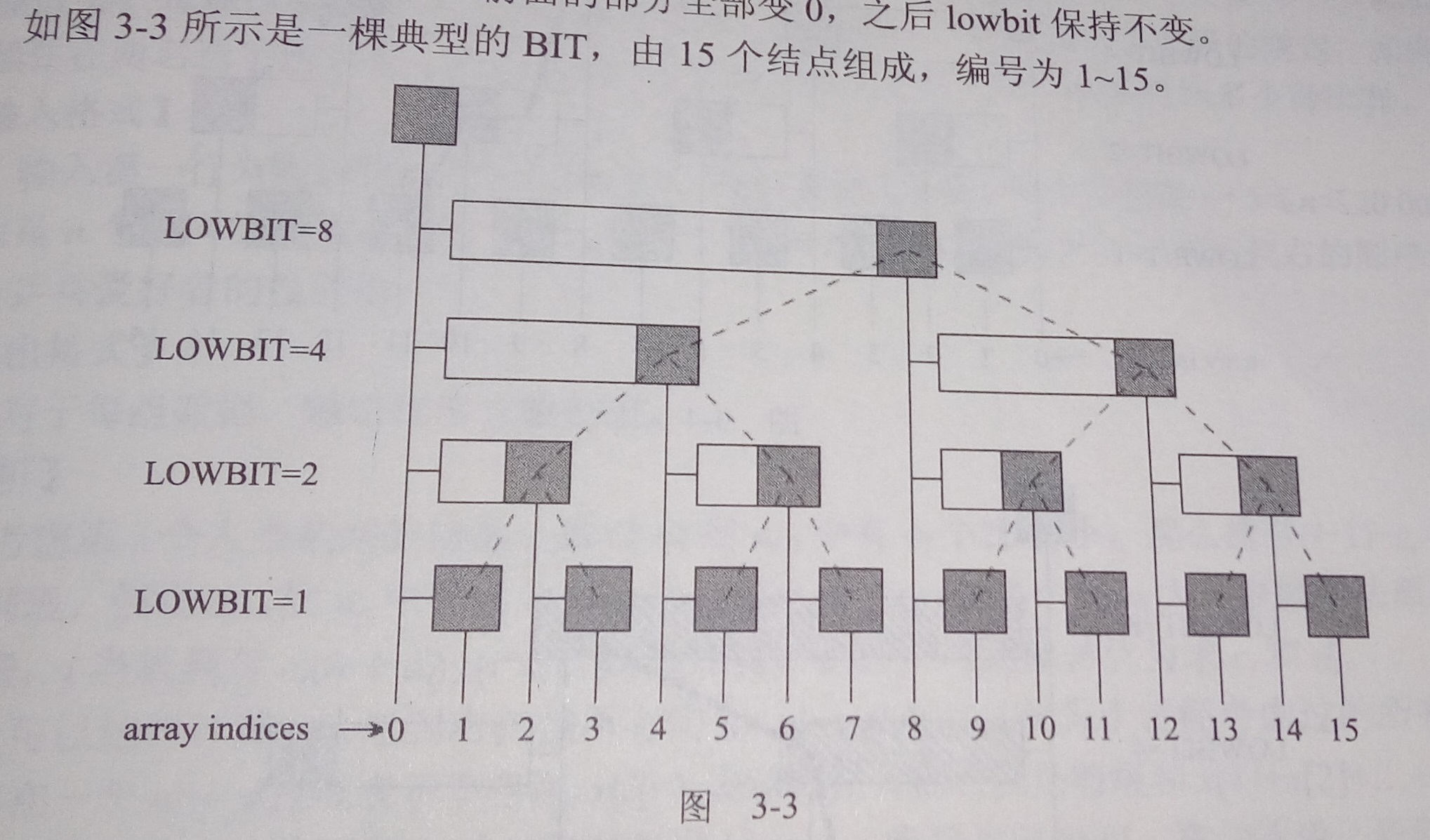
利用了二进制，二分的思想的一个很巧妙的数据结构，一个lowbit(x):二进制表示下的最右边的一个1开始对应的数值。

那么如果一个节点的为x左孩子，父亲节点就是 x + lowbit(x)，如果是右孩子，父亲节点是 x-lowbit(x)；

图中白条部分就是辅助数组C对应的最底下的和。

1、那么一个前缀和有是怎样的呢？

　　就是从最底下开始，边往上走，边往左走。

2、修改单点呢？

　　从最底下开始，边往上走，边往下走。

LA2191:

题目链接：https://vjudge.net/contest/147973#problem/A

题意：

先给出一个数组，然后有两个操作

S x y 把第x个数改成y

M x y计算x~y个数的和

Source Code:

#include <bits/stdc++.h>

using namespace std;

inline int lowbit(int x)
{
    return x&-x;
}

struct FenwickTree
{
    int n;
    vector<int> C;

    void resize(int n)
    {
        this->n = n;
        C.resize(n+10);
    }
    void clear()
    {
        fill(C.begin(), C.end(), 0);
    }

    // 计算A[1]+A[2]+...+A[x] (x<=n)
    int sum(int x)
    {
        int ret = 0;
        while(x > 0)
        {
            ret += C[x];
            x -= lowbit(x);
        }
        return ret;
    }

    // A[x] += d (1<=x<=n)
    void add(int x, int d)
    {
        while(x <= n)
        {
            C[x] += d;
            x += lowbit(x);
        }
    }
};

FenwickTree f;
const int maxn = 200000+5;
int a[maxn];

int main()
{
   // freopen("in.txt","r",stdin);
    int n;
    int cases = 0;
    while(scanf("%d",&n),n)
    {
        if(cases>0) puts("");
        printf("Case %d:
",++cases);
        f.resize(n);
        f.clear();
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&a[i]);
            f.add(i,a[i]);
        }

        char op[5];
        while(scanf("%s",op)!=EOF)
        {
            if(!strcmp(op,"END"))
                break;
            if(op[0]=='M')
            {
                int x,y;
                scanf("%d%d",&x,&y);
                printf("%d
",f.sum(y)-f.sum(x-1));
            }
            if(op[0]=='S')
            {
                int x,y;
                scanf("%d%d",&x,&y);
                int add = y - a[x];
                a[x] = y;
                f.add(x,add);
            }
        }
    }

    return 0;
}

LA5902:

题目链接：https://vjudge.net/contest/147973#problem/B

题意：

XXX喜欢看电影，他有好多好多的影碟，每个影碟都有个独立的编号。开始是从下往上影碟的顺序是n~1，他每次拿出影碟的时候，你需要输出压在该影碟上的有几个。（拿出后其他影碟顺序不变）看完影碟后，XXX会把影碟放在最上面。

分析：

把每个影碟放到一个考后的位置，这个位置有影碟，那么这里就是 1，否则是 0 ，每次询问，就是这个影碟所在的位置之前的前缀和，

把他放到前面去，当前位置置为 0 ，top 的位置 加 1，注意要记录每个影碟的所在位置。

Source Code：

#include <bits/stdc++.h>

using namespace std;


inline int lowbit(int x)
{
    return x&-x;
}

struct FenwickTree
{
    int n;
    vector<int> C;

    void resize(int n)
    {
        this->n = n;
        C.resize(n);
    }
    void clear()
    {
        fill(C.begin(), C.end(), 0);
    }

    // 计算A[1]+A[2]+...+A[x] (x<=n)
    int sum(int x)
    {
        int ret = 0;
        while(x > 0)
        {
            ret += C[x];
            x -= lowbit(x);
        }
        return ret;
    }

    // A[x] += d (1<=x<=n)
    void add(int x, int d)
    {
        while(x <= n)
        {
            C[x] += d;
            x += lowbit(x);
        }
    }
};

FenwickTree f;
const int maxn = 100000+5;
int pos[maxn];


int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    int t;
    scanf("%d",&t);

    while(t--)
    {
        int n,q;
        scanf("%d%d",&n,&q);
        f.resize(maxn*2);
        f.clear();

        for(int i=1; i<=n; i++)
        {
            f.add(maxn+i,1);
            pos[i] = maxn+i;
        }

        int top = maxn;
        while(q--)
        {
            int x;
            scanf("%d",&x);
            int tmp = pos[x];
            if(q!=0)
                printf("%d ",f.sum(tmp-1));
            else printf("%d",f.sum(tmp-1));
            f.add(tmp,-1);
            f.add(top--,1);
            pos[x] = top + 1;
        }
        puts("");
    }
    return 0;
}

LA4329

题目链接：https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&category=26&page=show_problem&problem=2330

题意：

一条大街上住着n个乒乓球爱好者，经常组织比赛。每个人都有一个技能值ai，每场比赛需要3个人：两名选手和一名裁判。规定裁判位置必须在两个选手的中间，而且技能值也必须在两个选手的中间，问一共能组织多少种比赛。

分析：

和上题类似，每个技能值有的话为 1 ，否则为 0 ，每一个点都可以做裁判，那么他能组织多少场比赛？

a₁~a_i-1 有 ci个比 ai 小，a_i+1~a_n有di个比他小，乘法加法原理，ci(n-i-di) + di(i-ci-1)。

#include <bits/stdc++.h>

using namespace std;


inline int lowbit(int x) {
    return x&-x;
}

struct FenwickTree {
    int n;
    vector<int> C;

    void resize(int n) {
        this->n = n;
        C.resize(n);
    }

    void clear() {
        fill(C.begin(),C.end(),0);
    }

    //计算A[1] + A[2] + ... +A[n]
    int sum(int x) {
        int ret = 0;
        while(x>0) {
            ret +=C[x];
            x -=lowbit(x);
        }
        return ret;
    }

    // A[x] +=d;
    void add(int x,int d) {
        while(x<=n) {
            C[x] +=d;
            x +=lowbit(x);
        }
    }
};

const int maxn = 20000 + 5;
int n;
int a[maxn];
FenwickTree f;
int c[maxn],d[maxn];

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int maxa  = 0;
        scanf("%d",&n);
        for(int i=1;i<=n;i++) {
            scanf("%d",&a[i]);
            maxa = max(maxa,a[i]);
        }

        f.resize(maxa);
        f.clear();

        for(int i=1;i<=n;i++) {
            f.add(a[i],1);
            c[i] = f.sum(a[i]-1);
        }

        f.clear();
        for(int i=n;i>=1;i--) {
            f.add(a[i],1);
            d[i] = f.sum(a[i]-1);
        }

        long long ans = 0;
        for(int i=1;i<=n;i++) {
            ans +=(long long)c[i]*(n-i-d[i]) + (long long)(i-c[i]-1)*d[i];
        }
        printf("%lld
",ans);
    }

    return 0;
}