题意:求AC率,x/y 的最小值,x是区间数字的种类数,y是区间的长度。
分析:
二分答案比率。ans,
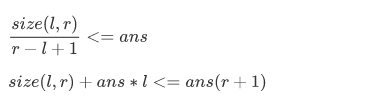
动态插入结点,一些区间的size会发生变化,是那些前面暂时没有新的结点的区间 size + 1。
ans*l,每一个区间只有一个ans*l,只与 l 相关,线段树单点更新。
用线段树维护区间的最小值。最小值小于 ans,二分左移。
#include <bits/stdc++.h> using namespace std; const int maxn = 60005; const int eps = 1e-9; int a[maxn]; int last[maxn]; double tree[maxn<<2],add[maxn<<2]; void pushdown(int root) { tree[root<<1]+=add[root]; tree[root<<1|1]+=add[root]; add[root<<1]+=add[root]; add[root<<1|1]+=add[root]; add[root]=0; } void update(int l,int r,int L,int R,int root,double k) { if(l<=L&&R<=r) { tree[root]+=k; add[root]+=k; return ; } if(add[root]>eps)pushdown(root); int mid=L+R>>1; if(r<=mid)update(l,r,L,mid,root<<1,k); else if(l>mid)update(l,r,mid+1,R,root<<1|1,k); else { update(l,mid,L,mid,root<<1,k); update(mid+1,r,mid+1,R,root<<1|1,k); } tree[root]=min(tree[root<<1],tree[root<<1|1]); } double query(int l,int r,int L,int R,int root) { if(l<=L&&R<=r) return tree[root]; if(add[root]>eps)pushdown(root); int mid=L+R>>1; if(r<=mid)return query(l,r,L,mid,root<<1); else if(l>mid)return query(l,r,mid+1,R,root<<1|1); else return min(query(l,mid,L,mid,root<<1),query(mid+1,r,mid+1,R,root<<1|1)); tree[root]=min(tree[root<<1],tree[root<<1|1]); } int main() { //freopen("in.txt","r",stdin); int t; scanf("%d",&t); while(t--) { int n; scanf("%d",&n); for(int i=1; i<=n; i++) scanf("%d",&a[i]); double l = 0,r=1.0; for(int g=0; g<20; g++) { double mid = (l+r)/2.0; memset(tree,0,sizeof(tree)); memset(add,0,sizeof(add)); memset(last,0,sizeof(last)); int flag = 0; for(int i=1; i<=n; i++) { update(last[a[i]]+1,i,1,n,1,1); update(i,i,1,n,1,mid*i); last[a[i]] = i; double k = query(1,i,1,n,1); if(k<=(double)mid*(i+1)) { flag=1; break; } } if(flag!=1) l = mid; else r = mid; } printf("%.10lf ",l); } return 0; }