后缀数组模版

要不是因为机房有做得特别快的大佬的话，我估计早就要wate了

先放一篇大佬的博客啊

1180: [视频]后缀数组【模板】后缀排序

洛谷P3809

时间限制: 2 Sec  内存限制: 512 MB
提交: 294  解决: 159
[提交] [状态] [讨论版] [命题人:admin]

题目描述

题目背景
这是一道模板题。
 

题目描述
给出一个字符串，把这个字符串的所有非空后缀从小到大排序后，按顺序输出后缀的第一个字符在原串中的位置。
 

输入输出格式
输入格式：
一个字符串
输出格式：
一行，共n个整数，表示答案。
 
输入输出样例
输入样例#1：
ababa
输出样例#1：

5 3 1 4 2

 后缀数组真的是一个老难老难的东西了，首先我们要了解一些资料，然后在这里我会放上来供参考啊！

链接：https://pan.baidu.com/s/1lBsfN6F4u7Q0jbuygw-Q0w
提取码：omdc （中间的链接请拖到浏览器直接查看）

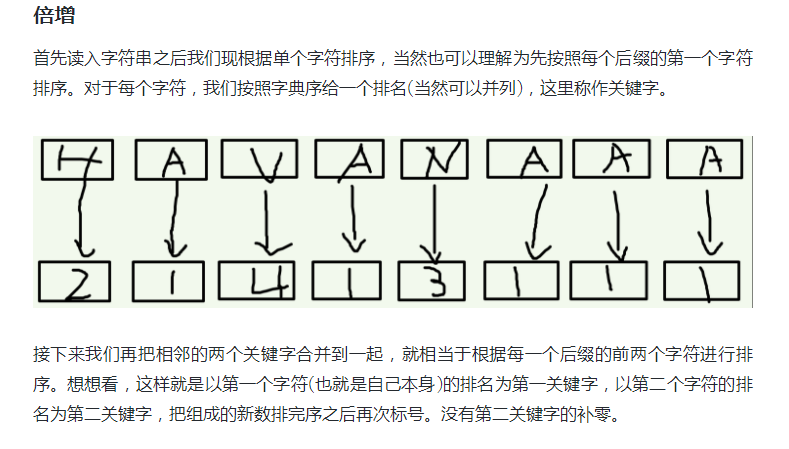
然后我们需要了解一个叫基数排序的东西，处理几位数就有几个关键字

因为是基数排序，所以下面提到的第一关键字和第二关键字都是因为基数排序的使用

比如说我们要处理一串两位数：

14 15 23 67 89 

第一次我们先处理个位的排序，得出来的就是：

3 4 5 7 9（这个目前作为第一关键字）

然后我们处理十位的排序，得出来的就是：

1 1 2 6 8（然后现在这个作为第一关键字）

3 4 5 7 9（这个作为第二关键字）

也就是说先处理的会作为第二关键字，后处理的作为第一关键字

然后我又认真的看了一遍模拟过程，就是说我们先处理个位按照个位处理一个排序，然后再处理十位，按照十位处理一个排序，处理百位也是同样的道理

这个我不过多解释还是自己看swf解释吧，本质是桶排

然后接下来我们进入正式的后缀数组的讲解，真的是一个太恶心的东西了，我不会DC3的做法，我只会倍增，目前来说

• 好的我们先认识两个数组啊
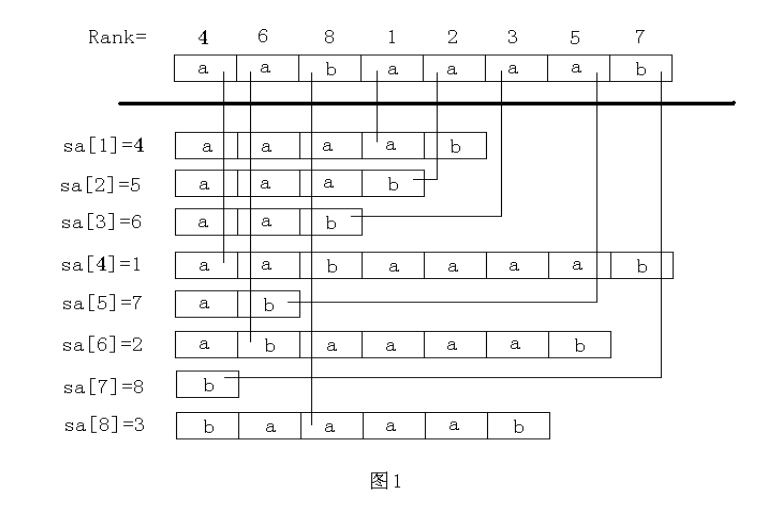
• 后缀数组：sa[i]就表示排名为i的后缀的起始位置的下标
• 名次数组：rank[i]就表示起始位置的下标为i的后缀的排名

简单来说就是，后缀数组就是”排第几的是谁“，名次数组就是”你排第几“

这两个数组为互逆运算，下面的图一就可以很清楚的看出来（以下图片来自罗穗骞的后缀数组论文）

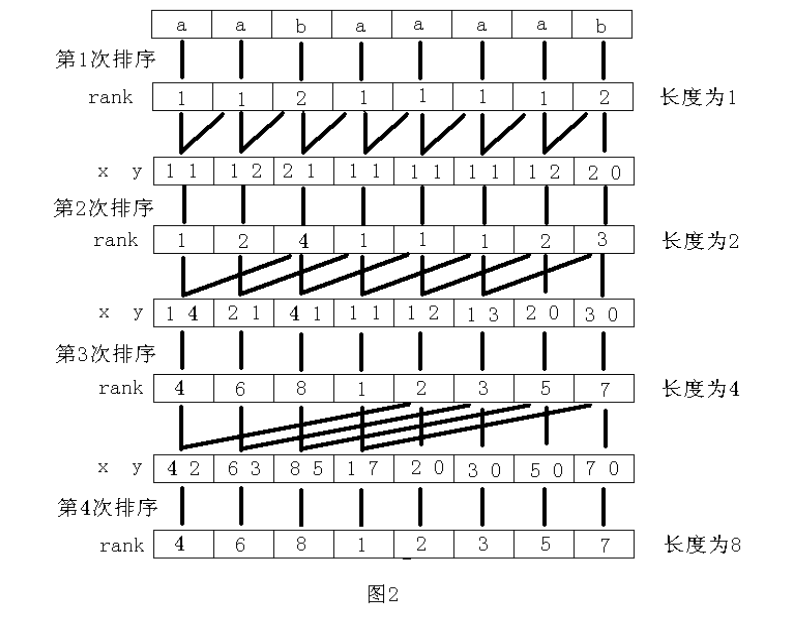
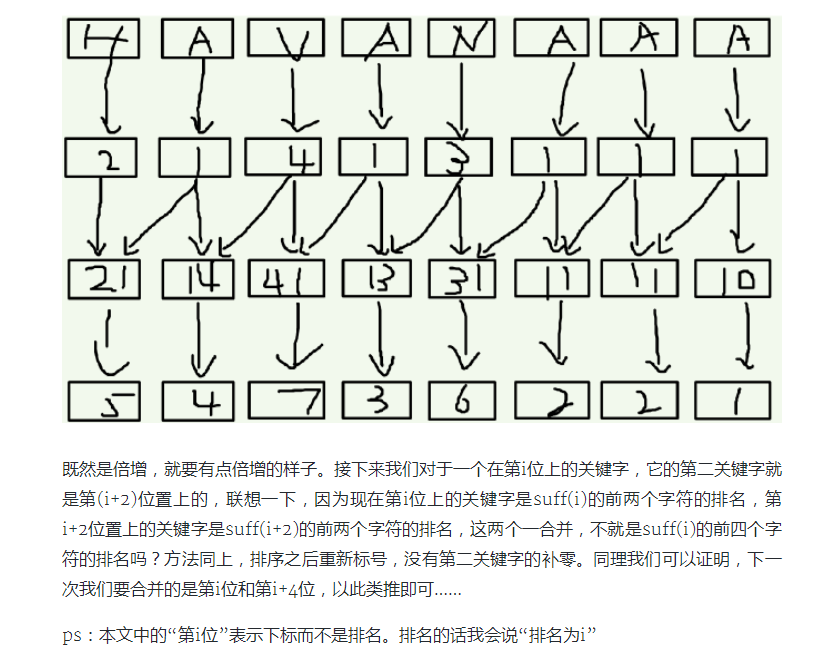
然后就要介绍倍增算法

下面是倍增的实现过程

大概到这里的话，我们基本思路的实现就已经讲完了，接下来我copy xMinh大佬的倍增实现过程，这个写的实现过程要详细一些

大佬的博客要详细很多，所以到这里我们就已经把基本上要处理的都处理完了

然后的话，我们先来看一下这道题的代码实现，然后再讲一个新的东西，毕竟这个新的东西在这道题里面还没有太大的用处

（注释版，就是一些细节咯，我建议看一下吧，毕竟这个还是挺难的我觉得）

/*https://xminh.github.io/2018/02/27/%E5%90%8E%E7%BC%80%E6%95%B0%E7%BB%84-%E6%9C%80%E8%AF%A6%E7%BB%86(maybe)%E8%AE%B2%E8%A7%A3.html*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<iostream>
using namespace std;
/*
Rank[i]表示编号为i的排名，第i个元素的第一关键字  
sa[i]表示排名为i的编号 
sa数组和Rank数组是相匹配的  
Rsort[i]计数排序的桶 
pos[i]表示当前第二关键字已经排好序时第i名第二关键字所对应的第一关键字位置
cnt[i]
排序时：表示当前排序中编号为i的排名
排序后：表示调整Rank前的排名
*/
int sa[1100010],Rank[1100010],Rsort[1100010];/*rank是系统的内置数组*/
int a[11000010],cnt[1100010],pos[1100010];
bool cmp(int x,int y,int k){return cnt[x]==cnt[y] && cnt[x+k]==cnt[y+k];}
char s[1100010];
void Suffix(int n,int m) 
{
    int k=1,p=0,len;//已经处理好的长度 有多少个不同的后缀 
    for(int i=1;i<=n;i++) Rank[i]=a[i];
    memset(Rsort,0,sizeof(Rsort));
    /*处理k=1*/
    for(int i=1;i<=n;i++) Rsort[Rank[i]]++;
    for(int i=1;i<=m;i++) Rsort[i]+=Rsort[i-1];
    for(int i=n;i>=1;i--) sa[Rsort[Rank[i]]--]=i;/*计数排序，设置好Rank和sa数组
    基数排序和计数排序是不一样的*/
    /*第一关键字和第二关键字都是用于基数排序的，先排的作为第二关键字*/
    /*基数排序：类似于桶排序，
    先按个位的数字一个个放入0~9的桶里，再按顺序从0~9取出来，（当然如果你是从大到小就是9~0啦！）    
    接着再按十位的数字一个个放入桶里，按顺序取出来，如果是两位数，这时我们得到的就是答案！    
    以此类推，一直循环到最后一位    
    计数排序：就更高级了。这里优化了一下， 就是我们在基数排序所用的桶，是记录他出现的次数，
    然后累加(写入代码就是Rsort[i]+=Rsort[i-1])，这样我们得到的Rsort[i]数组里就是不大于i的个数，就是他的排名了!*/
    /*基数排序的思想，计数排序的优化*/ 
    
    for(int k=1;k<n;k<<=1)/*k表示长度，k<<=1等于k*2*/
    /*
    每次循环
    都将两个长度k子串合并为一个长度为2^k的串
    其中前k个字符构成的子串的排名为第一关键字，后k个字符为第二关键字
    并求出合并后的字符串的排名 
    */
    /*每次排名得到一共有多少个排名p，由p优化m的值*/
    {
        len=0;/*先排序第二关键字*/ 
        /*
        在上一轮中，第一关键字已经排好了， 此时只需要排第二关键字即可。 
        y数组是第二关键字排序的结果，存储的是2k长度的字符串的第一关键字的下标 
        n-k到n-1中所有的元素第二关键字为0 
        */
        for(int i=n-k+1;i<=n;i++) pos[++len]=i;
        /*
        pos[i]表示第二关键字排名为i的数，第一关键字的位置 
        第n-k+1到第n位是没有第二关键字的 所以排名在最前面 
        */
        for(int i=1;i<=n;i++) if(sa[i]>k) pos[++len]=sa[i]-k;
        /*
        排名为i的数 在数组中是否在第k位以后
        如果满足(sa[i]>k) 那么它可以作为别人的第二关键字，就把它的第一关键字的位置添加进pos就行了
        所以i枚举的是第二关键字的排名，第二关键字靠前的先入队 
        */
        for(int i=1;i<=n;i++) cnt[i]=Rank[pos[i]];
        memset(Rsort,0,sizeof(Rsort));
        for(int i=1;i<=n;i++) Rsort[cnt[i]]++;/*因为上一次循环已经算出了这次的第一关键字，所以直接加就可以了*/
        for(int i=1;i<=m;i++) Rsort[i]+=Rsort[i-1];/*第一关键字排名为1~i的数有多少个*/
        for(int i=n;i>=1;i--) sa[Rsort[cnt[i]]--]=pos[i];/*更新sa数组*/
        /*
        因为y的顺序是按照第二关键字的顺序来排的 
        第二关键字靠后的，在同一个第一关键字桶中排名越靠后 
        基数排序 */
        for(int i=1;i<=n;i++) cnt[i]=Rank[i];/*记录之前的排名*/
        p=1; Rank[sa[1]]=1;/*初始化*/
        for(int i=2;i<=n;i++)
        {
            if(!cmp(sa[i],sa[i-1],k)) p++;
            /*因为sa[i]已经排好序了，所以可以按排名枚举，生成下一次的第一关键字 */
            Rank[sa[i]]=p;
        }
        if(p==n) break; m=p;/*这里就不用122了，因为都有新的编号了*/
    }
    for(int i=1;i<n;i++) printf("%d ",sa[i]);
    printf("%d
",sa[n]);
}
int main() 
{
    scanf("%s",s+1); int len=strlen(s+1);
    for(int i=1;i<=len;i++) a[i]=s[i]-'a'+1;/*方便处理*/
    Suffix(len,300);/*'z'是122 ,为了保险设置为130*/
    return 0;
}

（非注释版，可以清晰的看到倍增算法的简洁）

/*https://xminh.github.io/2018/02/27/%E5%90%8E%E7%BC%80%E6%95%B0%E7%BB%84-%E6%9C%80%E8%AF%A6%E7%BB%86(maybe)%E8%AE%B2%E8%A7%A3.html*/
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<iostream>
using namespace std;
int sa[1100010],Rank[1100010],Rsort[1100010];
int a[11000010],cnt[1100010],pos[1100010];
bool cmp(int x,int y,int k){return cnt[x]==cnt[y] && cnt[x+k]==cnt[y+k];}
char s[1100010];
void Suffix(int n,int m) 
{
    int k=1,p=0,len;
    for(int i=1;i<=n;i++) Rank[i]=a[i];
    memset(Rsort,0,sizeof(Rsort));
    for(int i=1;i<=n;i++) Rsort[Rank[i]]++;
    for(int i=1;i<=m;i++) Rsort[i]+=Rsort[i-1];
    for(int i=n;i>=1;i--) sa[Rsort[Rank[i]]--]=i;
    for(int k=1;k<n;k<<=1)
    {
        len=0;
        for(int i=n-k+1;i<=n;i++) pos[++len]=i;
        for(int i=1;i<=n;i++) if(sa[i]>k) pos[++len]=sa[i]-k;
        for(int i=1;i<=n;i++) cnt[i]=Rank[pos[i]];
        memset(Rsort,0,sizeof(Rsort));
        for(int i=1;i<=n;i++) Rsort[cnt[i]]++;
        for(int i=1;i<=m;i++) Rsort[i]+=Rsort[i-1];
        for(int i=n;i>=1;i--) sa[Rsort[cnt[i]]--]=pos[i];
        for(int i=1;i<=n;i++) cnt[i]=Rank[i];
        p=1; Rank[sa[1]]=1;
        for(int i=2;i<=n;i++)
        {
            if(!cmp(sa[i],sa[i-1],k)) p++;
            Rank[sa[i]]=p;
        }
        if(p==n) break; m=p;
    }
    for(int i=1;i<n;i++) printf("%d ",sa[i]);
    printf("%d
",sa[n]);
}
int main() 
{
    scanf("%s",s+1); int len=strlen(s+1);
    for(int i=1;i<=len;i++) a[i]=s[i]-'a'+1;
    Suffix(len,300);
    return 0;
}

 好的，我刚刚有提到说就是我要讲一个东西，一个新的东西，一个很恶心的证明过程，但是似乎不能在这道题起到半点作用

---

但是，既然他在我们后面做题用到了，我就提及一下吧（折腾子串是后缀数组当中常见的）

先看一个叫做子串的东西，专业术语（来自罗穗骞）

好的接下来的转自（xMinh大佬的博客）

其实这个所谓的新东西啊，其实就是我们的后缀数组的一些性质，然后下面的是证明过程

放一下代码

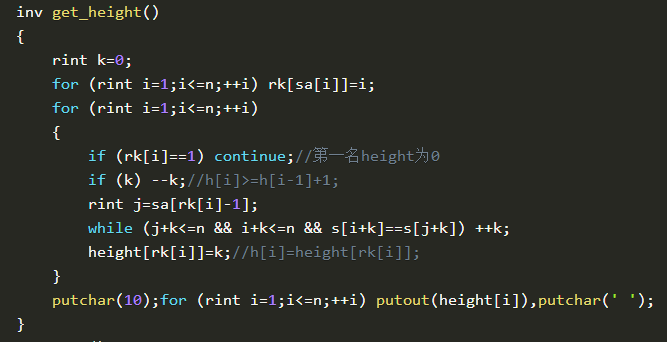
下面是（罗穗骞论文的最长公共前缀）

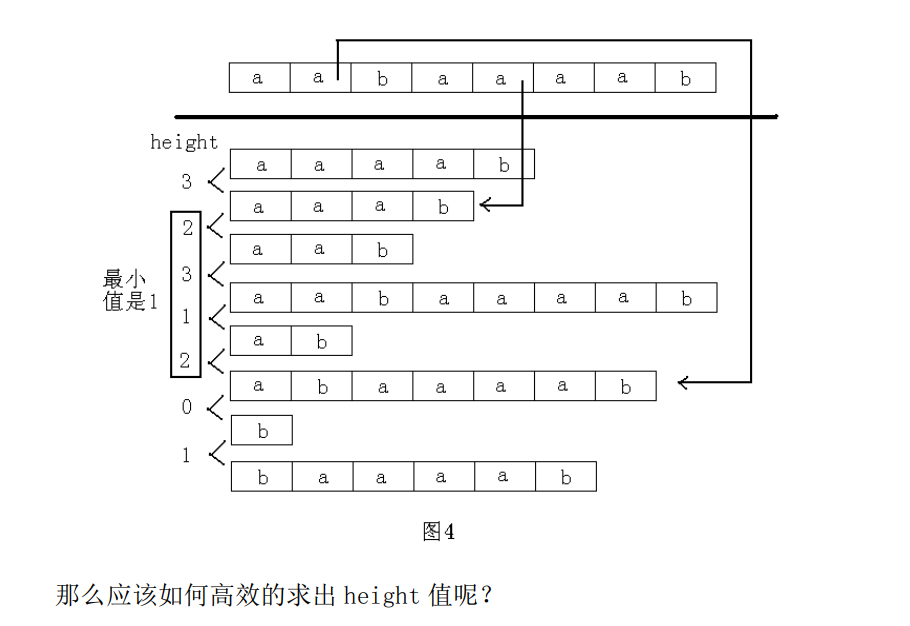
很快就会发现，我下面发的题都和这个性质有着密切的联系