FFT感性瞎扯

为了自己以后再用FFT时不再一脸懵X，本蒟蒻决定感性理解一下FFT。

FFT可以干啥？

把两个多项式乘在一起。

具体地说，对于两个多项式$f:f(x)=Sigma_{i=0}^n f_i x^i$和$g:g(x)=Sigma_{i=0}^m g_i x^i$，得到一个多项式$h:h(x)=Sigma_{x=0}^{n+m}Sigma_{i=0}^x f(i)g(x-i)$。

显然，如果暴力的话，是$O(n^2)$的。

但是，FFT可以做到$O(nlog_2n)$！

我们一点一点把它扯个不明不白。

Part1.复数

只需要记住一点结论：

复数相乘时，模长相乘，辐角相加。

比如说，对于两个极角表示法的复数$u(u_l,u_{ heta})$与$v(v_l,v_{ heta})$，有$w=uv=(u_l v_l,u_{ heta}+v_{ heta})$

Part2.单位根

（以下，默认$n$为$2$的整数幂）

我们把单位圆上的某个复数$(cos(2kpi/n),sin(2kpi/n))$称作单位根$omega_n^k$。换句话说，就是极角表示法下的复数$(1,2kpi/n)$。当然，因为是在单位圆上，我们可以只关注它的辐角$(2kpi/n)$。

如图。


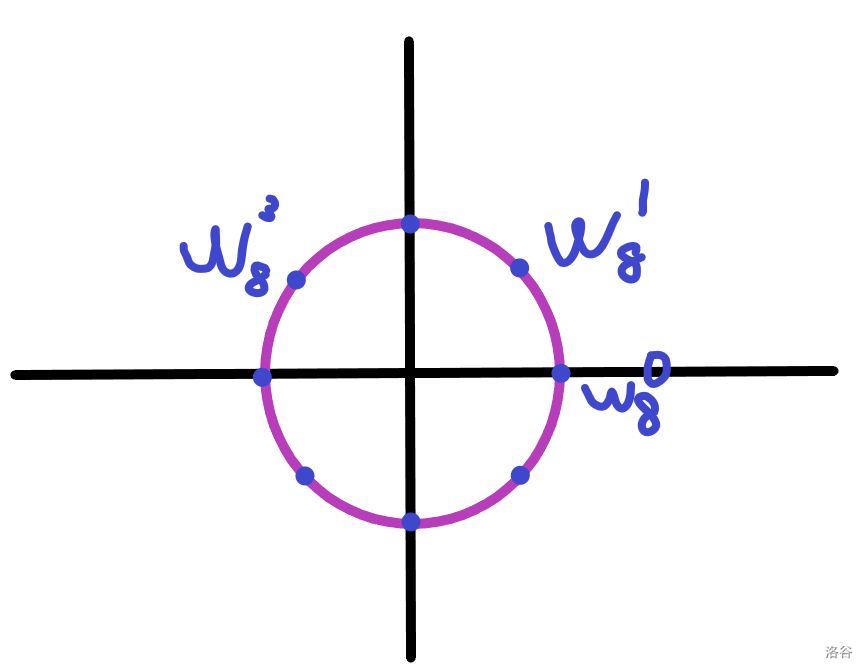
结论1：$omega_n^k=omega_n^{k+n}$。

类比正负角。可以感性理解一下，就等于绕了一整圈，度数$>2pi$的角。有$omega_n^k=2kpi/n=2kpi/n+2pi=2kpi/n+2npi/n=2(k+n)pi/n=omega_n^{k+n}$

结论2：$omega_n^k=-omega_n^{k+n/2}$

等于绕了半圈的角。

结论3：当$k$为偶数时，$omega_n^k=omega_{n/2}^{k/2}$。这是最重要的结论。

有$omega_n^k=2kpi/n=2(k/2)pi/(n/2)=omega_{n/2}^{k/2}$

Part3.DFT

显然，$n+1$个点可以唯一确定一个$n$次多项式。

而我们如果知道$f$和$g$上各$n+m+1$个点，就可以在$O(n)$时间內把它们乘在一起。对于每个点$(x,f(x))$与$(x,g(x))$，新点即为$(x,f(x)g(x))$。

DFT解决的就是将多项式$f$由系数表达转为点值表达。

开始推式子：

$f(x)$

$=a_0+a_1x+a_2x^2+...+a_nx^n$

$=(a_0+a_2x^2+...+a_nx^n)+(a_1x+a_3x^3+...+a_{n-1}x^{n-1})$

$=(a_0+a_2x^2+...+a_nx^n)+x(a_1+a_3x^2+...+a_{n-1}x^{n-2})$

令$f1(x)=a_0+a_2x+...+a_nx^{n/2}$，$f2(x)=a_1+a_3x+...+a_{n-1}x^{n/2}$

则$f(x)=f1(x^2)+xf2(x^2)$。

令$x=omega_n^k(k<n/2)$。

则$f(omega_n^k)$

$=f1((omega_n^k)^2)+omega_n^kf2((omega_n^k)^2)$

$=f1(omega_n^{2k})+omega_n^kf2(omega_n^{2k})$

$=f1(omega_{n/2}^k)+omega_n^kf2(omega_{n/2}^k)$

再令$x=omega_n^{k+n/2}(k<n/2)$。

则$f(omega_n^{k+n/2})$

$=f1((omega_n^{k+n/2})^2)+omega_n^{k+n/2}f2((omega_n^{k+n/2})^2)$

$=f1(omega_n^{2k+n})+omega_n^{k+n/2}f2(omega_n^{2k+n})$

$=f1(omega_n^{2k})+omega_n^{k+n/2}f2(omega_n^{2k})$

$=f1(omega_{n/2}^k)-omega_n^kf2(omega_{n/2}^k)$

注意到什么了吗？

**$f(omega_n^k)$与$f(omega_n^{k+n/2})$，结果只有最后一项的符号不同！！！！！！**

然后就可以分治了。只要知道$f1(omega_{n/2}^k)$与$f2(omega_{n/2}^k)$的值，就可以直接得出$f(omega_n^k)$与$f(omega_n^{k+n/2})$！！！

因此我们可以令$f1(omega_{n/2}^k)$成为新的$f(x)$，进一步递推。

Part4.IDFT

只需要将DFT中的$omega_n^k$改为$omega_n^{-k}$即可。别忘了最后记得除上数组长度！！！

Part5.代码:

#include<bits/stdc++.h>
using namespace std;
const int MAXN=4000000;
int n,m,lim=1,t,res[MAXN];
const double pi=acos(-1);
struct cp{
 double x,y;
 cp(double u=0.0,double v=0.0){
  x=u,y=v;
 }
 friend cp operator +(const cp &lv,const cp &rv){
  return cp(lv.x+rv.x,lv.y+rv.y);
 }
 friend cp operator -(const cp &lv,const cp &rv){
  return cp(lv.x-rv.x,lv.y-rv.y);
 }
 friend cp operator *(const cp &lv,const cp &rv){
  return cp(lv.x*rv.x-lv.y*rv.y,lv.x*rv.y+lv.y*rv.x);
 }
}f[MAXN],g[MAXN];
void FFT(cp *a,int sz,int inv){
 if(sz==1)return;
 int md=sz>>1;
 static cp b[MAXN];
 for(int i=0;i<md;i++)b[i]=a[i<<1],b[i+md]=a[(i<<1)+1];
 for(int i=0;i<sz;i++)a[i]=b[i];
 FFT(a,md,inv),FFT(a+md,md,inv);
 for(int i=0;i<md;i++){
  cp x=cp(cos(2*pi*i/sz),inv*sin(2*pi*i/sz));
  b[i]=a[i]+x*a[i+md],b[i+md]=a[i]-x*a[i+md];
 }
 for(int i=0;i<sz;i++)a[i]=b[i];
}
int read(){
 char c=getchar();
 int x=0;
 while(c>'9'||c<'0')c=getchar();
 while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
 return x;
}
int main(){
 n=read(),m=read();
 for(int i=0,t;i<=n;i++)f[i].x=read();
 for(int i=0,t;i<=m;i++)g[i].x=read();
 while(lim<=n+m)lim<<=1;
 FFT(f,lim,1),FFT(g,lim,1);
 for(int i=0;i<lim;i++)f[i]=f[i]*g[i];
 FFT(f,lim,-1);
 for(int i=0;i<lim;i++)res[i]=(int)(f[i].x/lim+0.5);
 for(int i=0;i<=n+m;i++)printf("%d ",res[i]);
 return 0;
}

Part6.非递归

在FFT时，一个位置上的数的最终位置，是把其位置的二进制表达翻转后的新位置。

即有:

$(7)_{10}=(111)_2 ightarrow(111)_2=(7)_{10}$

$(13)_{10}=(1101)_2 ightarrow(1011)_2=(11)_{10}$

$(22)_{10}=(10110)_2 ightarrow(01101)_2=(13)_{10}$

显然，当长度不同时，一个数可能翻转到不同的位置。

而它的终点位置，可以如此递推：

for(int i=0;i<lim;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));

其中，$lim$是长度，$lg=log_2(lim)$。

Part7.最终非递归代码：

#include<bits/stdc++.h>
using namespace std;
const int MAXN=4000000;
int n,m,lim=1,t,res[MAXN],lg,rev[MAXN];
const double pi=acos(-1);
struct cp{
 double x,y;
 cp(double u=0.0,double v=0.0){
  x=u,y=v;
 }
 friend cp operator +(const cp &lv,const cp &rv){
  return cp(lv.x+rv.x,lv.y+rv.y);
 }
 friend cp operator -(const cp &lv,const cp &rv){
  return cp(lv.x-rv.x,lv.y-rv.y);
 }
 friend cp operator *(const cp &lv,const cp &rv){
  return cp(lv.x*rv.x-lv.y*rv.y,lv.x*rv.y+lv.y*rv.x);
 }
}f[MAXN],g[MAXN];
int read(){
 char c=getchar();
 int x=0;
 while(c>'9'||c<'0')c=getchar();
 while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
 return x;
}
void FFT(cp *a,int tp){
 for(int i=0;i<lim;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
 for(int md=1;md<lim;md<<=1){
  cp rt=cp(cos(pi/md),tp*sin(pi/md));
  for(int stp=md<<1,pos=0;pos<lim;pos+=stp){
   cp w=cp(1,0);
   for(int i=0;i<md;i++,w=w*rt){
    cp x=a[pos+i],y=w*a[pos+md+i];
    a[pos+i]=x+y;
    a[pos+md+i]=x-y;
   }
  }
 }
}
int main(){
 n=read(),m=read();
 while(lim<=(n+m))lim<<=1,lg++;
 for(int i=0;i<lim;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
 for(int i=0;i<=n;i++)f[i].x=read();
 for(int i=0;i<=m;i++)g[i].x=read();
 FFT(f,1),FFT(g,1);
 for(int i=0;i<lim;i++)f[i]=f[i]*g[i];
 FFT(f,-1);
 for(int i=0;i<lim;i++)res[i]=(int)(f[i].x/lim+0.5);
 for(int i=0;i<=n+m;i++)printf("%d ",res[i]);
 return 0;
} 

完结撒傅里叶~~~