SAM是Suffix Automaton 萨菲克斯自动马桶的缩写,其中文翻译是后缀自动机。
顾名思义,其是一个自动机。SAM接受一个串,当且仅当其是母串 \(S\) 的后缀。
这里我们给出一些定义:
所有使用黑板粗体格式的字符 \(\mathbb{S}\),表示集合;
所有使用大写格式的字符 \(S\),表示字符串;
所有使用黑体格式的字符 \(\mathbf{s}\),表示字符型变量;
所有使用正体格式的字符 \(\text{s}\),表示一种定义;
所有使用小写格式的字符 \(s\),表示整型变量;
所有被代码框框起来的字符 s,表示 s 这个字符。ss 之类,可能表示字符串,也可能表示一段代码,视具体情形而定。
所有无任何格式的字符 s,表示一种专有名词。
定义字符串的下标从 \(0\) 开始(若没有特殊说明)。
定义 \(\text{pre}_S(i)\) 为 字符串 \(S\) 长度为 \(i\) 的前缀。若已经定义了 \(S\),也可以简写成 \(\text{pre}(i)\) 或 \(\text{pre}_i\)。
定义 \(\text{suf}_S(i)\) 同理,表示后缀。
定义母串 \(S\) 为后缀自动机所作用的串。
定义 \(|S|\) 符号表示串 \(S\) 的长度。更多的时候,会专门定义一个 \(n\) 来表示。同时,其也可以被用于表示一个集合中元素的数量。
O.后缀自动机
模板的讲解。
首先,若我们暴力地想建出SAM,明显点数是 \(O(|S|^2)\) 的。
唯一的优化方式即为缩减状态数。
定义 \(\text{endpos}_S(T)\) 是一个串 \(T\) 在串 \(S\) 中所有出现的位置的结尾下标。明显,其是一集合。例如,若 \(T\) 为 ab,\(S\) 为 abab,则 \(\text{endpos}_S(T)=\{1,3\}\)。在指明 \(S\) 的时候可以忽略下标。
我们发现,在 \(S\) 的众多子串中,有很多串的 \(\text{endpos}\) 集合是相等的。例如,在上文的例子中,ab 和 b 的 \(\text{endpos}\) 集合就是相同的。
我们把两个串 \(T_1,T_2\) \(\text{endpos}\) 集合相等的关系称作 \(\text{endpos}\) 等价,符号表示为 \(T_1\equiv_ST_2\)。指明 \(S\) 时可忽略下标。
我们发现,通过上述的 \(\equiv\) 关系,我们可以将 \(S\) 的所有子串分作众多 \(\text{endpos}\) 等价类,简称类。
则有如下定理:
这是非常显然的——更长的串都匹配上了,更短的串还能匹配不上吗?
由 \((1)\),便可得到定理 \((2)\):
\(\boxed{\text{定理2:对于两个串}T_1,T_2(|T_1|\geq|T_2|),\text{endpos}(T_1)\subseteq\text{endpos}(T_2)\text{ 或 }\text{endpos}(T_1)\cup\text{endpos}(T_2)=\varnothing}\)
实际上是 \((1)\) 的逆命题。证明类似。
由 \((1)\) 和 \((2)\),可以得到 \((1)\) 更强的推论:
\(\boxed{\text{定理3:等价类中所有串按照长度从大到小排序,后一个是前一个的长度减一的后缀}}\)
于是我们定义 \(\min(\mathbb{S})\) 为一集合 \(\mathbb{S}\) 中长度最短的串,\(\max(\mathbb{S})\) 为最长的。
考虑往 \(\max(\mathbb{S})\)(设其为 \(P\)) 开头添加一个字符,则会得到一个新的串 \(Q\)。明显,\(\text{endpos}(Q)\subset\mathbb{S}\)。而添加不同的字符,便会得到不同的 \(Q\)——明显这些 \(Q\),因为其长度相等而又不完全相同,故其 \(\text{endpos}\) 集合全都无交。并且,所有这样的 \(Q\) 的 \(\text{endpos}\) 集合的并会得到 \(\mathbb{S}\)。
这也意味着这样的操作是一个划分操作——每个 \(\mathbb{S}\) 中的串归入且仅归入一个集合。明显,划分操作是有父子关系的,故所有集合实际上构成了一棵树,称其为 parent tree。同时,在划分的时候,\(\mathbb{S}\) 中会至少有一个元素被分到了大小为 \(1\) 的集合。
而这就意味着,总节点数不会超过 \(2n\)(有 \(n\) 个大小为 \(1\) 的集合;根集合大小为 \(n\),每次划分至少损失掉一个元素)!那就意味着,如果我们有较快的算法建出parent tree,是可以存得下其中所有东西的!
但是,知道有parent tree这种东西,又有什么用呢?
我们将看到,parent tree中所有节点,刚好可以被看作是自动机上节点! 空串节点可被看作是DAG的源点,所有包含母串的集合 \(\mathbb{S}\) 都是终止节点。可以发现,终止节点形成parent tree中一条从源点到叶子的链。
在自动机中,我们需要保证,一条从源点到某个点 \(i\) 的路径上所有边上的字符依次拼接起来会刚好得到 \(i\) 点所对应集合里所有的串,也即自动机上的边上储存的是字符;而parent tree,因为在分析中我们是往前面不停添加字符,所以边上存的都是字符串。在parent tree上沿着边向子树中走,相当于往当前集合中的所有串的开头插入一个字符串;在自动机上沿着边走,则相当于往当前集合中所有串的结尾插入一个字符。这部分也可以类别AC自动机和fail树的关系(尽管二者的相似之处很少,除了都是一个自动机和一个树以外就没别的相同之处了)
我们已经保证自动机的点数是 \(O(n)\) 的了;但是如何保证其边数也符合要求呢?
事实上,其边数也是 \(O(n)\) 的。
我们考虑母串的全部后缀。明显,只需要保证每个后缀都能有一条从根到其代表节点的路径,即可拍胸脯保证这是一个合法的SAM了(因为这就是SAM的定义呀)。与此同时,我们不仅可以从源点出发正着跑路径,也可以从终止节点出发倒着跑路径——二者是等价的。
我们考虑对自动机求出其任意一棵生成树,并通过往生成树中加入新边来复原出自动机。然后,我们考虑遍历每个终止节点,并且按照某种顺序遍历该终止节点对应集合内所有的字符串。
如果对于其中一个串,存在一条从根到该终止节点的路径来表示该串,显然该串已经被check过合法了,可以跳过;
否则,即不存在一条这样的路径(尚未被添加入生成树张成的自动机中)。我们考虑将这条路径上尚未被添加的边(因为已经有一棵生成树,所以最多只有一条缺失的边)加入自动机中。这时,其parent tree中父亲、祖父,乃至所有祖先的集合中,当前字符串的后缀字符串,其也有一条路径同时被铺出来了(尽管不一定是原本自动机中的路径,但是只要有一条路径就行了)。之后,考虑再check下一个串即可。可以发现,此过程添加的边不会超过 \(|\text{endpos}(\mathbb{S})|\) 的大小。而所有后缀中,一条边最多只会被加一次,所以总边数就是后缀数量,也即 \(O(n)\) 的。
后缀自动机的构造是在线的,增量的。这意味着可以在任意时刻,往任意节点后面添加字符(也就意味着可以很容易用它来实现树上SAM,或是多串SAM之类)。
一个典型的SAM长这样:
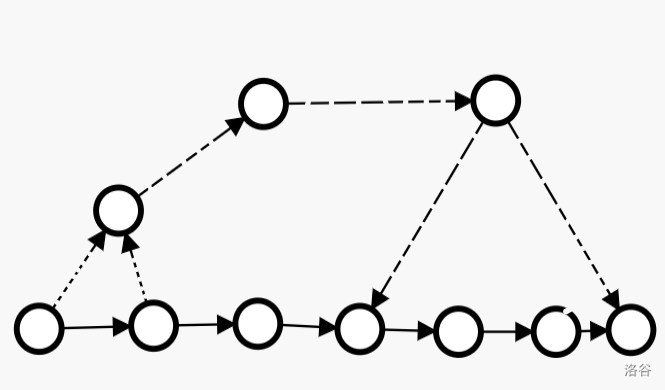
如图,底下一溜节点是原串的前缀,它们是一定存在于自动机里的(即parent tree中一整条终止节点路径)。而上面的节点,以及那些虚线的边,是不一定存在,也不一定是这么连接的。
我们定义一个集合 \(\mathbb{S}\) 的 \(\max(\mathbb{S})\) 的长度为 \(\text{len}(\mathbb{S})\)。明显,parent tree中,集合 \(\mathbb{S}\) 有且仅有一个父亲,称作 \(\text{fa}(\mathbb{S})\)。则,\(|\min(\mathbb{S})|\),应为 \(\text{len}\Big(\text{fa}(\mathbb{S})\Big)+1\),依照我们上面关于添加字符的分析。这就意味着我们只需对于集合 \(\mathbb{S}\) 储存其父亲和其最大串的长度就能知道其最小串的长度了。它们将在建SAM时派上大用处。
以下,会照着程序解释。
struct Suffix_Automaton{int ch[26],len,fa;}t[N<<1];//a SAM has 2n nodes!!!
int cnt=1;
int Add(int x,int c){//add a character c after node x,return the index.
int xx=++cnt;//the index of the newly-added node
t[xx].len=t[x].len+1;//the maximal length of strings in xx.
for(;x&&!t[x].ch[c];x=t[x].fa)t[x].ch[c]=xx;
if(!x){t[xx].fa=1;return xx;}
int y=t[x].ch[c];
if(t[y].len==t[x].len+1){t[xx].fa=y;return xx;}
int yy=++cnt;t[yy]=t[y];
t[yy].len=t[x].len+1;
t[y].fa=t[xx].fa=yy;
for(;x&&t[x].ch[c]==y;x=t[x].fa)t[x].ch[c]=yy;
return xx;
}
首先,记原来的串为 \(S\),加完新字符后的串为 \(S'\)。显然,依照我们上述推论,\(S'\) 自身所对应的状态是一定在自动机里的,但是它目前不在,所以建一个新点 \(xx\) 表示 \(S'\) 串本身,其长度为 \(|S|+1\)。
在添加完一个 \(\mathbf{c}\) 后(注意此处 \(\mathbf{c}\) 是一个字符,所以使用黑体),明显受到影响的只有 \(S'\) 的后缀(或者说 \(S\) 的所有后缀再加上 \(\mathbf{c}\))。
然后,不断地跳 \(x\) 的父亲。因为 \(x\) 是旧串的母串节点,所以 \(x\) 的所有祖先就全是终止节点,即所有旧串的后缀。若当前的 \(x\) 没有一个 \(\mathbf{c}\) 的儿子,该后缀后面加上 \(\mathbf{c}\) 就能得到 \(S'\) 的后缀,故在自动机上连一条边 \((x,xx)\)(回忆一下,后缀自动机的边的意义是在结尾处添加字符),然后继续遍历其祖先。
如果一路跳最终跳到了根,显然整个串中都没有出现过 \(\mathbf{c}\)。因此直接令 \(x\) 的父亲为根即可。
否则,即其存在一个 \(\mathbf{c}\) 儿子,即为代码中的 \(y\)。
若 t[y].len==t[x].len+1 成立,则应有 \(\max(y)=\max(x)+\mathbf{c}\)。而 \(x\) 是旧串后缀,故 \(y\) 表示新串后缀。因此,\(y\) 与 \(xx\) 定义相同。但是 \(xx\) 在一路跳上去的过程中已经被设作了一堆东西的儿子,所以为了不再把它设一遍,我们直接认 \(y\) 作父亲。
于是,下面就有 t[y].len!=t[x].len+1。而因为parent tree中的长度是随着深度增加而递增的,故实际上是t[y].len>t[x].len+1。
此时,考虑 \(\max(x)+\mathbf{c}\)。明显,其应该属于 \(y\),但是其并不属于新串后缀(不然会直接跳到它所属节点上)。也即,\(y\) 节点所属集合中,不全是可以添加 \(\mathbf{c}\) 的串。因而,我们必须将 \(y\) 分作两个集合,一个作为 \(x\) 的 \(\mathbf{c}\) 儿子,一个变成了 \(xx\) 的兄弟,也即 \(x\) 的孙子。
我们选择,另开一个新节点 \(yy\) 作为 \(x\) 的 \(\mathbf{c}\) 儿子,然后用 \(y\) 本身作为 \(yy\) 的儿子。则 \(x\) 以及 \(x\) 祖先中所有出现过的 \(y\) 边(明显其应该是一条从 \(x\) 往上的链)都应该被更换成 \(yy\),然后令 \(\text{len}(yy)=\text{len}(x)+1\)。
那问题来了,为什么我们不交换 \(y\) 和 \(yy\) 的定义呢?因为 \(y\) 链可能在 \(x\) 以下还有部分,但从 \(x\) 出发只能找到其父亲上的 \(y\) 链,却找不到儿子处的 \(y\) 链。所以我们只能将父端的 \(y\) 换成 \(yy\),而不能将子端的 \(y\) 换成 \(yy\)。
于是以上就是模板的全部内容。
可以发现,后缀自动机的复杂度是 \(O(n|\Sigma|)\) 的,其中 \(|\Sigma|\) 是字符集大小。通过使用 map<int,int> 来储存儿子们,可以将复杂度优化至 \(n\log|\Sigma|\)。但是对于平时的 \(26\) 个字母来说,用了反而会更慢。