Description
有一张N×m的数表，其第i行第j列（1 < =i < =礼，1 < =j < =m）的数值为
能同时整除i和j的所有自然数之和。给定a，计算数表中不大于a的数之和。
Input
输入包含多组数据。
输入的第一行一个整数Q表示测试点内的数据组数，接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。
Output
对每组数据，输出一行一个整数，表示答案模2^31的值。
Sample Input
2
4 4 3
10 10 5
4 4 3
10 10 5
Sample Output
20
148
148
HINT
1 < =N．m < =10^5 ， 1 < =Q < =2×10^4
题解：
%%%popoqqq。设：
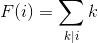，所以：
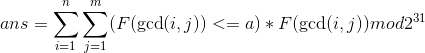
先不考虑a的影响，设：
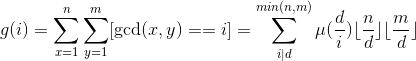。所以
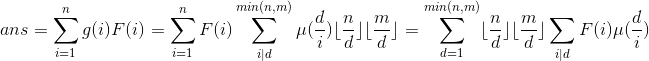
然后考虑询问，
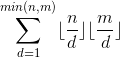可以分块，
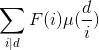，逆向枚举每个合法的i，对其对应的倍数d加上
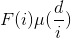，分块的同时查询一下前缀和即可。
1 #include<cstdio> 2 #include<algorithm> 3 #define lowbit(x) ((-x)&x) 4 inline int read(){ 5 int s=0;char ch=getchar(); 6 while(ch>'9'||ch<'0') ch=getchar(); 7 while(!(ch>'9'||ch<'0')) s=s*10+ch-48,ch=getchar(); 8 return s; 9 } 10 inline int min(int a,int b){return a<b?a:b;} 11 const int N=(int )1e5+10; 12 int c[N]; 13 void add(int x,int w){ 14 for(int i=x;i<N;i+=lowbit(i)) 15 c[i]+=w; 16 } 17 int query(int x){ 18 int s=0; 19 for(int i=x;i;i-=lowbit(i)) 20 s+=c[i]; 21 return s; 22 } 23 int F[N],mobius[N]; 24 int pri[N],K,opt[N],mar; 25 bool vis[N]; 26 inline void init(){ 27 F[1]=1;mobius[1]=1; 28 opt[1]=1; 29 for(int i=2;i<mar;i++){ 30 /// printf("%d ",i); 31 if(!vis[i]) pri[++K]=i,F[i]=i+1,mobius[i]=-1; 32 for(int j=1;j<=K&&pri[j]*i<mar;j++){ 33 vis[i*pri[j]]=1; 34 if(i%pri[j]) F[pri[j]*i]=F[i]*(pri[j]+1),mobius[pri[j]*i]=-mobius[i]; 35 else{ 36 int t=i;while(t%pri[j]==0) t/=pri[j]; 37 F[pri[j]*i]=F[i]*pri[j]+F[t]; 38 mobius[pri[j]*i]=0; 39 break; 40 } 41 } 42 opt[i]=i; 43 } 44 } 45 int ans[N]; 46 int n[N],m[N],a[N],ops[N]; 47 int T; 48 bool cmp(int x,int y){ 49 return a[x]<a[y]; 50 } 51 bool F_cmp(int x,int y){ 52 return F[x]<F[y]; 53 } 54 inline void solve(int x) 55 { 56 for (int i=1,pos;i<=n[ops[x]];i=pos+1) 57 { 58 59 pos=min(n[ops[x]]/(n[ops[x]]/i),m[ops[x]]/(m[ops[x]]/i)); 60 ans[ops[x]]+=(n[ops[x]]/i)*(m[ops[x]]/i)*(query(pos)-query(i-1)); 61 } 62 } 63 int main(){ 64 65 T=read(); 66 for(int i=1;i<=T;i++){ 67 n[i]=read(),m[i]=read(),a[i]=read(); 68 if(n[i]>m[i]) n[i]^=m[i]^=n[i]^=m[i]; 69 ops[i]=i;mar=n[i]>mar?n[i]:mar; 70 } 71 mar++; init(); 72 std::sort(ops+1,ops+1+T,cmp); 73 std::sort(opt+1,opt+mar,F_cmp); 74 int now=0; 75 for(int i=1;i<=T;i++){ 76 while(F[opt[now+1]]<=a[ops[i]]){ 77 for(int j=opt[++now];j<mar;j+=opt[now]) 78 add(j,F[opt[now]]*mobius[j/opt[now]]); 79 } 80 solve(i); 81 } 82 for(int i=1;i<=T;i++){ 83 printf("%d ",ans[i]&0x7fffffff); 84 } 85 }