[WP]XCTF-notsequence

1、基本信息：32 位 ELF 文件

2、载入 IDA 后进入 main 函数

将输入的字符串经过 check1，check2 检查后，如果都通过而且 check1 返回值为 20 时正确输出

题目中提示 flag 为我们输入的值的 md5 值

3、进入两个函数

 

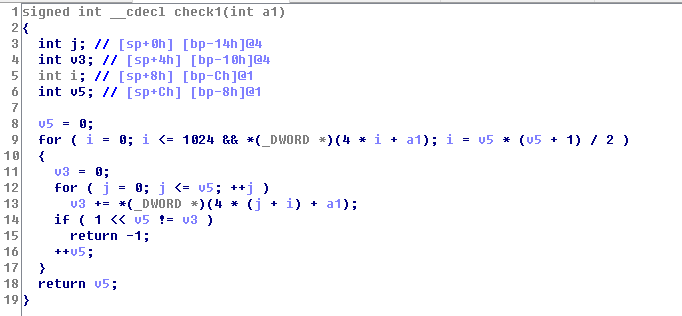
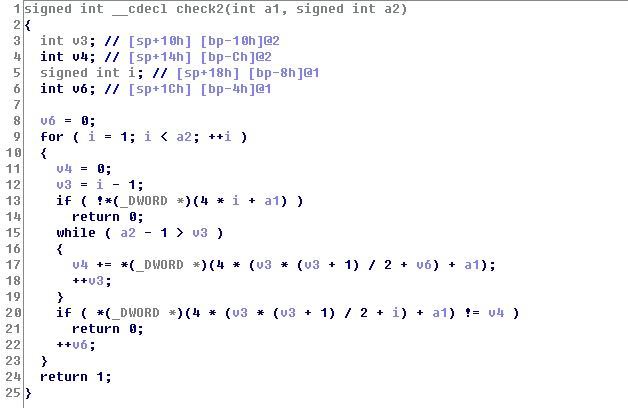
 将 check1, check2 函数重写

check1 检测是否每行之和是否为 2^(n-1) （n 为行数），之后将 i 赋值为 v5 * (v5 + 1) / 2 

check2 检测最后一行，如果想得到正确结果，那么第一次返回为 20，实际上检测的也就是最后一行的每个元素是否是前一列的元素之和

def check1(a1):
    i = 0                                   #两层循环，可以看做一个二维数组
    v5 = 0
    while True:
        v3 = 0
        j = 0
        while True:
            v3 += a1[i+j]                   #v3 = 每行数字之和
            if j > v5: break
            j += 1
        if v3 != (1 << v5): return -1       #v3 == 2^n
        v5 += 1
        i += v5 * (v5 + 1) // 2             #i = 0, 1, 3, 6, 10, 15 ...
        if i > 1024 or i > len(a1): break
    return v5

def check2(a1, a2): 
    v6 = 0
    for i in range(a2):
        v4 = 0
        v3 = i - 1
        if i > len(a1): return 0
        index = 0
        while True:
            index = v3 * (v3 + 1) // 2      #index = 第 i 行之前的元素总数
            v4 += a1[index + v6]            #下标index+v6，保存每列的和
            v3 += 1
            if v3 >= a2 - 1: break
        if a1[index + i] != v4: return 0    #第 20 行的下标为 i 的元素
        v6 += 1
    return 1

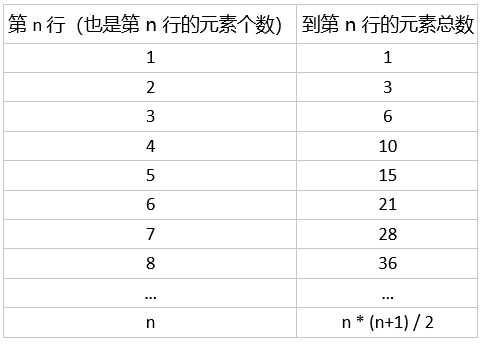
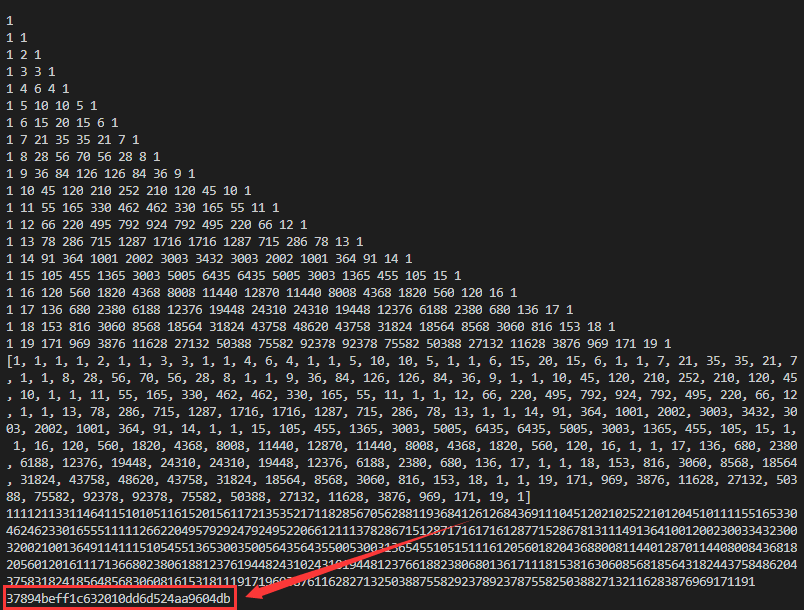
 4、而同时满足两个条件的是一个 20 行的杨辉三角

杨辉三角满足每个元素的值为两个顶角的值的和

 也就有了每个元素为此行之前的前一列元素之和

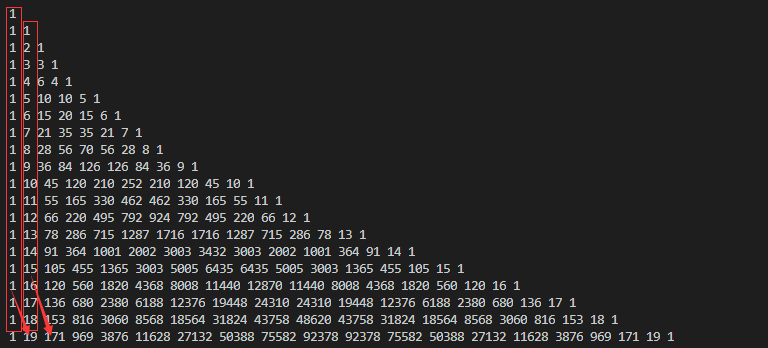
有关杨辉三角的性质：数学之美：杨辉三角(帕斯卡三角)的奇特性质

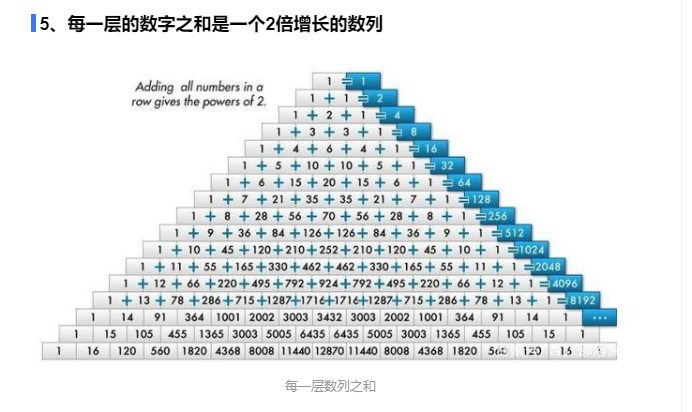
5、编写 EXP 生成杨辉三角，去除空字符和换行符，最后得到 md5 值

def main():
    a = []
    for i in range(21):         #check1 返回值为 20，因此需要生成 20 行的杨辉三角
        value = 0

        for j in range(i):
            index = (i-1) * (i-2) // 2          #j 从 0 开始计数，index 为每行之前的元素总数
            if j == 0 or j == i-1: value = 1
            else: 
                value = a[index+j-1] + a[index+j]
            a.append(value)
            print(value, end=' ')
        print()
    print(a)
    flag = ''
    for i in a:
        flag += str(i)
    print(flag)
    md = hashlib.md5(flag.encode())
    print(md.hexdigest())
    
main()