A. Uncowed Forces
【题意】给定公式,带入数值
【分析】按题目中说的来,注意精度
【代码】
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cmath>
using namespace std;
int main (void)
{
int w[5],m[5],s[5]={500,1000,1500,2000,2500};
int hs,hu;
double total=0.0;
for(int i=0;i<5;i++) cin>>m[i];
for(int i=0;i<5;i++) cin>>w[i];
cin>>hs>>hu;
for(int i=0;i<5;i++)
total+=max(0.3*s[i],((1-(m[i]/250.0))*s[i]-50*w[i]));
cout<<total+100*hs-50*hu;
}
B. More Cowbell
【题意】给定物品个数,箱子个数及每个物品的大小,每个箱子最多放两个物品,求最小的箱子大小。
【分析】从最大的物品开始放,每个箱子先放一个,放满一轮之后,将剩余的物品从小到大倒着放一遍,即编号为i 的物品跟编号为2*n-2*m+1-i的物品放在一个箱子里,记录最大值。
【代码】
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cmath>
using namespace std;
const int maxn=100005;
int s[maxn];
int main (void)
{
int n,m,maxs;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>s[i];
maxs=s[n];
for(int i=n-m;i>=0;i--)
maxs=max(maxs,s[i]+s[2*n-2*m+1-i]);
cout<<maxs<<endl;
}C. Alternative Thinking【题意】给定一组01串,可以将相邻的若干字符进行翻转(0->1,1->0),求翻转后,01交替(可以不连续)构成的子串的最大长度。
【分析】若只有一个字符与前一个字符相等,则以该字符为首,将该字符及后面的子串全部翻转,长度加一;若含有两个及两个以上,则将第一个与前一个字符相同的字符与最后一个与前一个字符相同的字符中间的子串看成一个整体,翻转后子串开头结尾将各增加一个【好绕】
【代码】
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
const int maxn=100005;
int main (void)
{
int n,result=1,cnt=0;
string s;
cin>>n>>s;
for(int i=1;i<n;i++)
{
if(s[i]!=s[i-1]) result++;
else cnt++;
}
if(cnt>2) cnt=2;
cout<<result+cnt<<endl;
}D. Moodular Arithmetic【题意】给定k,p,问有多少组映射满足
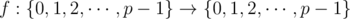
【分析】可知该映射满足双射,而对于已定的k,p,在定义域范围内x和k*x%p可以一个构成环,通过环中最小的元素获取这个环,得到环的个数,求出有多少组映射即可。
注意:
1.k=0;k=1时要特判
2.k!=0时,因为(k mod p)!=1,故必有f(0)=0;
【代码】
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
const int maxn=1000005;
typedef long long ll;
const ll mod=1e9+7;
int vis[maxn];
int k,p;
void dfs(ll x)
{
if(vis[x]) return;
vis[x]=1;
dfs(k*x%p);
}
int main (void)
{
int ans=0;
cin>>p>>k;
memset(vis,0,sizeof(vis));
ll result=1;
if(k==0)
{
for(ll i=0;i<p-1;i++)
{
result*=p;
result%=mod;
}
}
else if(k==1)
{
for(ll i=0;i<p;i++)
{
result*=p;
result%=mod;
}
}
else
{
for(ll i=0;i<p;i++)
{
if(vis[i]) continue;
dfs(i);
ans++;
}
for(int j=1;j<ans;j++)
{
result*=p;
result%=mod;
}
}
cout<<result<<endl;
}