【POJ】【2068】Art Gallery

计算几何/半平面交

---

　　裸的半平面交，关于半平面交的入门请看神犇博客：http://blog.csdn.net/accry/article/details/6070621

　　然而代码我是抄的proverbs的……

　　大体思路是这样的：（一个增量算法）

　　　　维护一个当前的半平面交的点集，每次用一条直线去cut它：

　　　　　　依次枚举“凸包”上的点，点在直线左边则保留下来了，否则就丢掉=。=

　　　　　　同时判一下如果“凸包”上连续的两个点分别在直线两侧，就加入这条“凸包”上的线段与直线的交点= =

　　　　然后新点集get！

　　最后求个面积>_>

　　有个trick是如果给的顺序是顺时针，需要反转成逆时针（用算多边形面积的方法就可以判断，如果是逆时针，面积为正）

Source Code
Problem: 1279        User: sdfzyhy
Memory: 720K        Time: 32MS
Language: G++        Result: Accepted

    Source Code

    //POJ 1279
    #include<cmath>
    #include<vector>
    #include<cstdio>
    #include<cstring>
    #include<cstdlib>
    #include<iostream>
    #include<algorithm>
    #define rep(i,n) for(int i=0;i<n;++i)
    #define F(i,j,n) for(int i=j;i<=n;++i)
    #define D(i,j,n) for(int i=j;i>=n;--i)
    #define pb push_back
    using namespace std;
    inline int getint(){
        int v=0,sign=1; char ch=getchar();
        while(ch<'0'||ch>'9'){ if (ch=='-') sign=-1; ch=getchar();}
        while(ch>='0'&&ch<='9'){ v=v*10+ch-'0'; ch=getchar();}
        return v*sign;
    }
    const int N=1e5+10;
    const double INF=1e9;
    typedef long long LL;
    /******************tamplate*********************/
    const double eps=1e-8;
    int dcmp(double x){return x>eps ? 1 : x<-eps ? -1 : 0;}
    struct Poi{
        double x,y;
        Poi(){}
        Poi(double x,double y):x(x),y(y){}
        void read(){scanf("%lf%lf",&x,&y);}
    }p[N],tp[N],s[N],o;
    typedef Poi Vec;
    Vec operator - (const Poi&a,const Poi &b){return Vec(a.x-b.x,a.y-b.y);}

    int n;
    double Cross(const Vec &a,const Vec &b){return a.x*b.y-a.y*b.x;}
    double getarea(Poi *p,int n){
        double ans=0.0;
        F(i,1,n) ans+=Cross(p[i]-o,p[i+1]-o);
        return ans*0.5;
    }
    Poi getpoint(const Poi &a,const Poi &b,const Poi &c,const Poi &d){
        Poi ans,tmp=b-a;
        double k1=Cross(d-a,c-a),k2=Cross(c-b,d-b);
        ans.x=a.x+tmp.x*k1/(k1+k2);
        ans.y=a.y+tmp.y*k1/(k1+k2);
        return ans;
    }

    void init(){
        n=getint();
        F(i,1,n) p[i].read();
        p[n+1]=p[1];
    }
    void Change(){
        F(i,1,n>>1) swap(p[i],p[n-i+1]);
        p[n+1]=p[1];
    }
    void getcut(){
        tp[1]=tp[5]=Poi(-INF,-INF);
        tp[2]=Poi(INF,-INF);
        tp[3]=Poi(INF,INF);
        tp[4]=Poi(-INF,INF);
        int num=4,size=0;
        F(i,1,n){
            size=0;
            F(j,1,num){
                if (dcmp(Cross(p[i+1]-p[i],tp[j]-p[i]))>=0)
                    s[++size]=tp[j];
                if (dcmp(Cross(p[i+1]-p[i],tp[j]-p[i]) * 
                         Cross(p[i+1]-p[i],tp[j+1]-p[i]))<0) 
                    s[++size]=getpoint(p[i],p[i+1],tp[j],tp[j+1]);
            }
            s[size+1]=s[1];
            F(j,1,size+1) tp[j]=s[j];
            num=size;
        }
        n=num;
    }
    int main(){
    #ifndef ONLINE_JUDGE
        freopen("1279.in","r",stdin);
        freopen("1279.out","w",stdout);
    #endif
        int T=getint();
        while(T--){
            init();
            if (dcmp(getarea(p,n))<=0) Change();
            getcut();
            printf("%.2f
",fabs(getarea(s,n)));
        }
        return 0;
    }

Art Gallery

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5805		Accepted: 2455

Description

The art galleries of the new and very futuristic building of the Center for Balkan Cooperation have the form of polygons (not necessarily convex). When a big exhibition is organized, watching over all of the pictures is a big security concern. Your task is that for a given gallery to write a program which finds the surface of the area of the floor, from which each point on the walls of the gallery is visible. On the figure 1. a map of a gallery is given in some co-ordinate system. The area wanted is shaded on the figure 2.

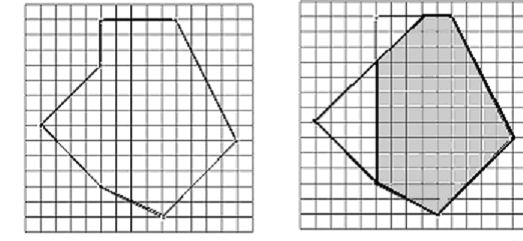
Input

The number of tasks T that your program have to solve will be on the first row of the input file. Input data for each task start with an integer N, 5 <= N <= 1500. Each of the next N rows of the input will contain the co-ordinates of a vertex of the polygon ? two integers that fit in 16-bit integer type, separated by a single space. Following the row with the co-ordinates of the last vertex for the task comes the line with the number of vertices for the next test and so on.

Output

For each test you must write on one line the required surface - a number with exactly two digits after the decimal point (the number should be rounded to the second digit after the decimal point).

Sample Input

1
7
0 0
4 4
4 7
9 7
13 -1
8 -6
4 -4

Sample Output

80.00

Source

Southeastern Europe 2002

[Submit]   [Go Back]   [Status]   [Discuss]