高精乘！！！

诶？！

好快！！！居然就到高精乘了！！！

欸！！！怎么说，其实高精乘和高精加都有关联都需要进位

还是先讲进位吧！！！

c[i+j-1]=a[i]*b[j]+x+c[i+j-1];//相当于乘积+上次乘积进位+原数
x=c[i+j-1]/10;
c[i+j-1]%10;

有没有轻松解决的感觉！！！

 就是如此简单。

高精乘的理解可以用竖式乘法进行理解

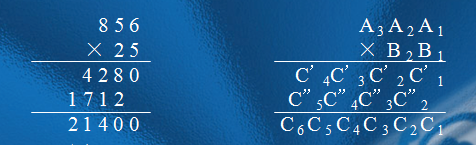
Such as this

从图中可以看出，乘法中乘法是错位相加，而进位就是如同高精加一样。

所以说它和之前的是相同的。

这里给出一道题目，洛谷的P1303

传送门

20%的小数据：

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int main()
{
    char a1[100],b1[100];
    int a[100],b[100],c[100],lena,lenb,lenc,i,j,x;
    memset(a,0,sizeof(a));
    memset(b,0,sizeof(b));
    memset(c,0,sizeof(c));
    scanf("%s",a1);
    scanf("%s",b1);
    lena=strlen(a1);lenb=strlen(b1);
    for (i=0;i<=lena-1;i++) a[lena-i]=a1[i]-48;
    for (i=0;i<=lenb-1;i++) b[lenb-i]=b1[i]-48;
for (i=1;i<=lena;i++)
    {
         x=0;
         for (j=1;j<=lenb;j++)
         {
           c[i+j-1]=a[i]*b[j]+x+c[i+j-1]; 
           c[i+j-1] %= 10;
         }
         c[i+lenb]=x;
    }
    lenc=lena+lenb;
    while (c[lenc]==0&&lenc>1)
        lenc--;
    for (i=lenc;i>=1;i--)
        cout<<c[i];
    cout<<endl;
    return 0;
}//告诉你什么叫没有对比就没有伤害

还有40%的数据：

#include<iostream>
#include<cstdio>
using namespace std;
int main(){
    long long a,b,c;
    cin>>a>>b;
    c=a*b;
    cout<<c;
    return 0;
}//没错，就是简单的乘法，震惊有木有！！！

直接扔题解，嘻嘻。

/*for(int i=1;i<=lena;i++)
      cout<<a[i]<<" ";
    cout<<endl;  
    for(int i=1;i<=lenb;i++)
      cout<<b[i]<<" ";*/ //调试； 
//好玩的小东西哦

骗你们的，嘻嘻。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
using namespace std;
const int Maxn=3005;
const int Maxm=6010;
string a1,b1;
int x=0,lena,lenb,lenc,a[Maxn],b[Maxn],c[Maxm];//x位数*y位数最多得到x+y位数
//不过要给数组留5左右的空间，方便它运算
//明明是防炸。 
int main()
{
    cin>>a1>>b1;//cin是各种输入皆可也就是说可以输入字符串，数组and so on
    //但是cin的缺点在于输入时间效率慢于scanf 
    lena=a1.length();
    lenb=b1.length();
    if(a1[0]=='0' || b1[0]=='0')
    {
        cout<<0;
        return 0;
}
//判断是否为零
 if(lena<lenb || (lena==lenb&&a1[0]<b1[0]))
   { swap(a1,b1);
    swap(lena,lenb);
}
//把较小的数放在b1，提高效率
//乘法中较小数在下面更容易求解（常识，笑） 
    if(a1[0]=='-'&&b1[0]!='-')
    {
        cout<<"-";
        a1[0]=' ';
        b1=' '+b1;
    }
    if(b1[0]=='-'&&a1[0]!='-')
    {
        cout<<"-";
        b1[0]=' ';
        a1=' '+a1;
    }
    if(a1[0]!='-'&&b1[0]!='-')
    {
        a1=' '+a1;
        b1=' '+b1;
    }
    if(a1[0]=='-'&&b1[0]=='-')
    {
        a1[0]=' ';
        b1[0]=' ';
}
//判断一下负数，a1[0]和b1[0]判断，i从1开始
    for(int i=1;i<=lena;i++)
      a[i]=a1[lena-i+1]-'0';
    for(int i=1;i<=lenb;i++)
      b[i]=b1[lenb-i+1]-'0';//逆序存储
    for(int i=1;i<=lenb;i++)
      for(int j=1;j<=lena;j++)
    {
     c[i+j-1]=c[i+j-1]+(b[i]*a[j]);
     c[i+j]+=c[i+j-1]/10;
     c[i+j-1]%=10;    
}
//最关键的一步，模拟乘法竖式计算
//b[i]*a[j]应存放在c[i+j]中，由于数组从1开始，所以需要减一
    int lenc=lena+lenb;
    while(lenc>0&&c[lenc]==0)
    {
    lenc--;
}
//消去开头的0
    for(int i=lenc;i>=1;i--)
      cout<<c[i];//输出 
    return 0;
}

好玩！！！