假设有这样的房间
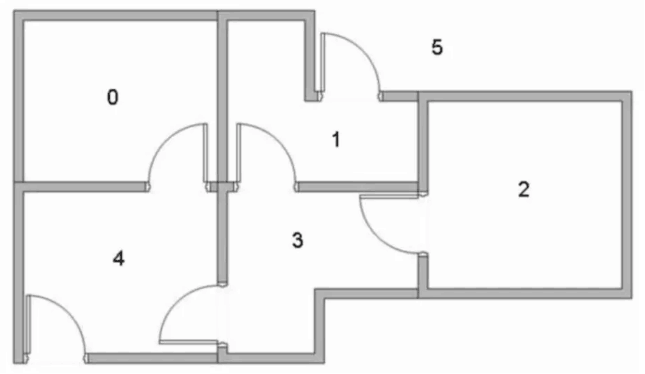
如果将房间表示成点,然后用房间之间的连通关系表示成线,如下图所示:
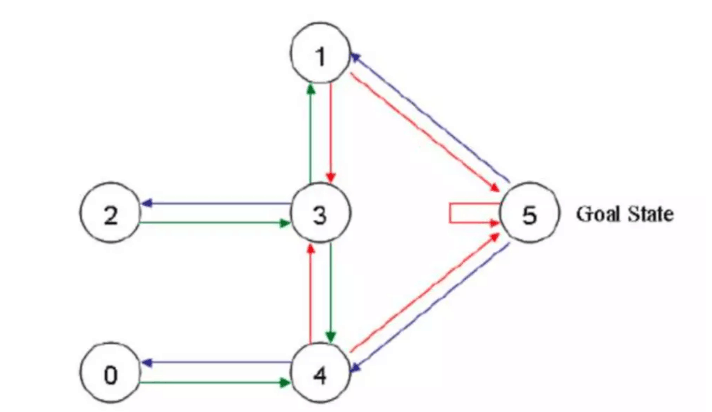
这就是房间对应的图。我们首先将agent(机器人)处于任何一个位置,让他自己走动,直到走到5房间,表示成功。为了能够走出去,我们将每个节点之间设置一定的权重,能够直接到达5的边设置为100,其他不能的设置为0,这样网络的图为:
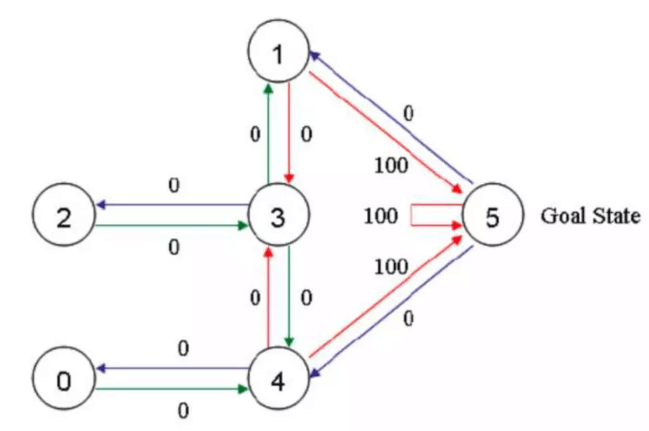
Qlearning中,最重要的就是“状态”和“动作”,状态表示处于图中的哪个节点,比如2节点,3节点等等,而动作则表示从一个节点到另一个节点的操作。
首先我们生成一个奖励矩阵矩阵,矩阵中,-1表示不可以通过,0表示可以通过,100表示直接到达终点:

同时,我们创建一个Q表,表示学习到的经验,与R表同阶,初始化为0矩阵,表示从一个state到另一个state能获得的总的奖励的折现值。

Q表中的值根据如下的公式来进行更新:
在上面的公式中,S表示当前的状态,a表示当前的动作,s表示下一个状态,a表示下一个动作,λ为贪婪因子,0<λ<1,一般设置为0.8。Q表示的是,在状态s下采取动作a能够获得的期望最大收益,R是立即获得的收益,而未来一期的收益则取决于下一阶段的动作。
所以,Q-learning的学习步骤可以归结为如下:

在迭代到收敛之后,我们就可以根据Q-learning来选择我们的路径走出房间。
看一个实际的例子,首先设定λ=0.8,奖励矩阵R和Q矩阵分别初始化为:

随机选择一个状态,比如1,查看状态1所对应的R表,也就是1可以到达3或5,随机地,我们选择5,根据转移方程:
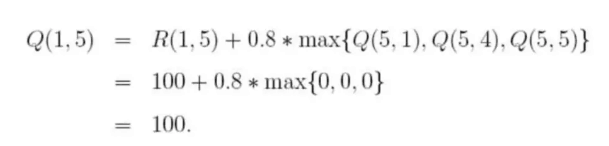
于是,Q表为:

这样,到达目标,一次尝试结束。
接下来再选择一个随机状态,比如3,3对应的下一个状态有(1,2,4都是状态3对应的非负状态),随机地,我们选择1,这样根据算法更新:

这样,Q表为:

经过不停的迭代,最终我们的Q表为:

我们不妨将Q表中的数转移到我们一开始的示意图中:

在得到Q表之后,我们可以根据如下的算法来选择我们的路径:

举例来说,假设我们的初始状态为2,那么根据Q表,我们选择2-3的动作,然后到达状态3之后,我们可以选择1,2,4。但是根据Q表,我们到1可以达到最大的价值,所以选择动作3-1,随后在状态1,我们按价值最大的选择选择动作1-5,所以路径为2-3-1-5.
2、代码实现
上面的例子可以用下面的代码来实现,非常的简单,直接贴上完整的代码吧:
import numpy as np
import random
r = np.array([[-1, -1, -1, -1, 0, -1], [-1, -1, -1, 0, -1, 100], [-1, -1, -1, 0, -1, -1], [-1, 0, 0, -1, 0, -1],
[0, -1, -1, 0, -1, 100], [-1, 0, -1, -1, 0, 100]])
q = np.zeros([6,6],dtype=np.float32)
gamma = 0.8
step = 0
while step < 1000:
state = random.randint(0,5)
if state != 5:
next_state_list=[]
for i in range(6):
if r[state,i] != -1:
next_state_list.append(i)
next_state = next_state_list[random.randint(0,len(next_state_list)-1)]
qval = r[state,next_state] + gamma * max(q[next_state])
q[state,next_state] = qval
print(q)
print(q)
# 验证
for i in range(10):
print("第{}次验证".format(i + 1))
state = random.randint(0, 5)
print('机器人处于{}'.format(state))
count = 0
while state != 5:
if count > 20:
print('fail')
break
# 选择最大的q_max
q_max = q[state].max()
q_max_action = []
for action in range(6):
if q[state, action] == q_max:
q_max_action.append(action)
next_state = q_max_action[random.randint(0, len(q_max_action) - 1)]
print("the robot goes to " + str(next_state) + '.')
state = next_state
count += 1
链接:https://www.jianshu.com/p/29db50000e3f