Convex hull(Convex envelope):
- In mathematics, the convex hull or convex envelope of a set X of points in the Euclidean plane or in a Euclidean space (or, more generally, in an affine space over the reals) is the smallest convex set that contains X.
Hessian matrix:
- In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables.

Bilinear function
- A function of two variables is bilinear if it is linear with respect to each of its variables. The simplest example is (f(x,y)=xy).
Point-to-set map(multivalued function)
- every input is associated with at least one output
sqrt(4) = 2,-2
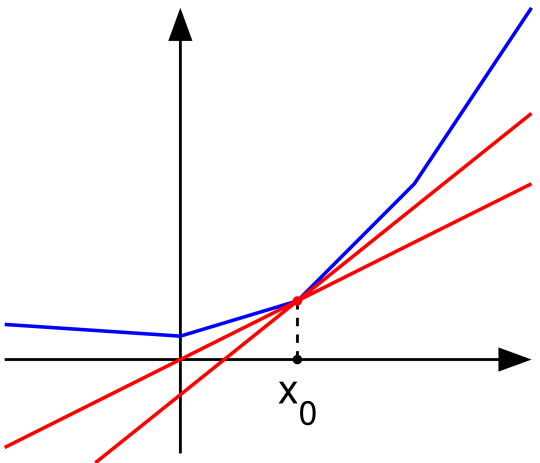
Subderivative(Subgradient)
- In mathematics, the subderivative, subgradient, and subdifferential generalize the derivative to functions which are not differentiable. The subdifferential of a function is set-valued. Such a function need not be differentiable at all points: For example, the absolute value function f(x)=|x| is nondifferentiable when x=0. However, as seen in the picture on the right, for any x0 in the domain of the function one can draw a line which goes through the point (x0, f(x0)) and which is everywhere either touching or below the graph of f. The slope of such a line is called a subderivative (because the line is under the graph of f).
判断函数是否为凸(多元)
- 如果函数的Hessian矩阵是半正定的,那么函数是凸的。
matlab求解Hessian矩阵
syms x y;
k = hessian(x*y,[x,y]);
Matlab判断矩阵正定
[p d] = eig(A); %如果所有的d都大于0,那么矩阵A正定
support function:
- In mathematics, the support function hA of a non-empty closed convex set A in {displaystyle mathbb {R} ^{n}} mathbb {R} ^{n} describes the (signed) distances of supporting hyperplanes of A from the origin. The support function is a convex function on {displaystyle mathbb {R} ^{n}} mathbb {R} ^{n}. Any non-empty closed convex set A is uniquely determined by hA.

- 待更新
总结:
- 前几天卡在一个v(y)的问题上卡了4天左右,后面又在判断一个具体的多元函数是否为凸上面卡了1天左右,期间发现了一个问问题不错的网站:math.stackexchange.com。总结一下就是感觉很盲目,应该把目前的情况列出来,然后分成小目标去完成。



