许多应用都需要处理有序的元素,但有时,我们不要求所有元素都有序,或是一定要一次就将它们排序,许多情况下,我们会收集这些元素里的最大值或最小值。
这种情况下一个合适的数据结构应该支持两种操作:插入元素、删除最大元素。
优先队列与栈和队列类似,但它有自己的奇妙之处。
在本文中,会讲解基于二叉堆的一种优先队列的经典实现方法(代码没有任何难度,主要是理解思想)。
一、关于堆
1、堆的定义:
数据结构二叉堆能很好地实现优先队列的操作。在二叉堆中,每个元素都要保证大于等于另外两个位置的元素,相应的,这些位置的元素又至少要大于等于数组中的另外两个元素。
将所有元素画成一颗二叉树,就能很容易看出这种结构。
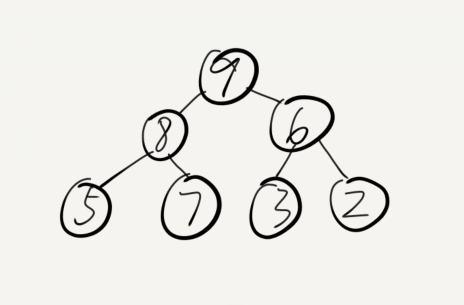
(图示1)
2、堆的算法:
在堆有序的过程中我们会遇到两种情况:
某个节点的优先级上升,我们需要由下至上恢复堆的顺序。
当某个节点的优先级下降,我们需要由上至下恢复堆的顺序。
在排序算法中,我们只通过私有辅助函数来访问元素:
1 private void exch(int i, int j) {
2 Key temp = pq[i];
3 pq[i] = pq[j];
4 pq[j] = temp;
5 }
6
7 private boolean less(int i, int j) {
8 return pq[i].compareTo(pq[j]) < 0;
9 }
①、由下至上的堆的有序化(上浮)
1 private void swim(int k) {// 二叉堆
2 while (k > 1 && less(k / 2, k)) {
3 exch(k / 2, k);
4 k = k / 2;
5 }
6 }
k/2即为k节点的父节点,当k大于k/2时交换两者,并继续与其父节点比较,直到找到合适的位置。
②、由上至下的堆的有序化(下沉)
1 private void sink(int k) {// 二叉堆
2 while (2 * k <= N) {
3 int j = 2 * k;
4 if (j < N && less(j, j + 1)) {
5 j++;
6 }
7 if (!less(k, j)) {
8 break;
9 }
10 exch(k, j);
11 k = j;
12 }
13 }
对于二叉树,2*k即为k的左子节点,将左右子节点进行比较,再将父节点与较大的子节点比较,如果子节点大于父节点,就将他们交换,并继续向下比较,直到找到合适的位置。
③、调整数组大小
如果不知道元素的个数,任意在初始化时造成空间的浪费。我们需要创造一个函数,用来调整数组的大小。
在插入方法中,如果空间已满,就将数组大小扩展为原来的两倍。在删除方法中,如果元素的个数小于数组长度的1/4,就将数组的长度减小一半。
1 private void resize(int n) {
2 Key[] temp = (Key[]) new Comparable[n + 1];
3 for (int i = 1; i <= N; i++) {
4 temp[i] = pq[i];
5 }
6 pq = temp;
7 L = n;
8 }
有了上面的方法,我们只需在插入和删除方法中加入判断语句即可。
④、多叉堆(了解即可)
在掌握了二叉堆的原理之后,将其改进为多叉堆只需要做几个改动。下面直接放代码,有兴趣的朋友可以自己动手。
1 private void swim(int k, int d) {// d叉堆:(k+d-2)/d为d叉堆第k个节点的父节点
2 while (k > 1 && less((k + d - 2) / d, k)) {
3 exch((k + d - 2) / d, k);
4 k = (k + d - 2) / d;
5 }
6 }
7
8 private void sinkM(int k, int d) {// d叉堆
9 while (d * k - (d - 2) <= N) {// d叉堆k节点的第一个子节点
10 int j = d * k - (d - 2);
11 int flag = k;
12 while (j <= N && j <= d * k + 1) {
13 if (less(flag, j)) {
14 flag = j;
15 }
16 j++;
17 }
18 if (flag == k) {// flag没有改变
19 break;
20 }
21 exch(k, flag);
22 k = flag;
23 }
24 }
二、堆排序(非降序):
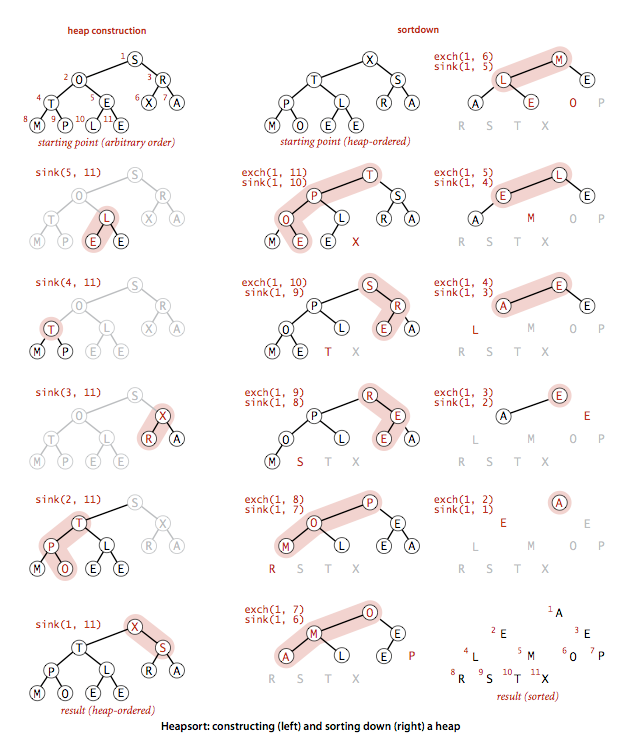
(示意图2)
堆排序的sink()方法经过修改sink(a,b)中a是被排序的元素,b为排序的最大范围(修改之前排序的最大范围为元素总个数)。
1 public void sort(Comparable[] a) {//堆排序
2 int n=N;
3 for(int k=n/2;k>=1;k--) {
4 sink(k,n);
5 }
6 while(n>1) {
7 exch(1,n--);
8 sink(1,n);
9 }
10 }
1、heap construction(堆的构造)
可以看到在for循环中,我们只扫描了数组一半元素,因为我们跳过了大小为1的子堆,每次对一个节点排序时,以该节点为根节点的子堆就是有序的,所以我们最后会得到一个堆有序的二叉堆。
2、sortdown(下沉排序)
下沉排序每次选出最大的元素放入数组空出的位置,这有点像选择排序,但所需的比较要小得多,因为堆提供了一种从未排序部分找到最大元素的有效方法。
三、java代码展示(所有代码)
1 public class MaxPQ<Key extends Comparable<Key>> {
2 private Key[] pq;
3 private static int N = 0;// 元素个数
4 private static int L;// 数组长度(不包括0)
5
6 public MaxPQ(int maxN) {
7 pq = (Key[]) new Comparable[maxN + 1];
8 L = maxN;
9 }
10
11 public boolean isEmpty() {
12 return N == 0;
13 }
14
15 public int size() {
16 return N;
17 }
18
19 public void insert(Key v) {// 二叉堆
20 if (N == L) {
21 resize(2 * N + 1);
22 System.out.println("resize Double");
23 }
24 pq[++N] = v;
25 swim(N);
26 }
27
28 public void insert(Key v, int d) {// d叉堆
29 if (N == L) {
30 resize(2 * N + 1);
31 System.out.println("resize Double");
32 }
33 pq[++N] = v;
34 swim(N, d);
35 }
36
37 public Key delMax() {
38 Key max = pq[1];
39 exch(1, N--);
40 pq[N + 1] = null;
41 sink(1);
42 if (N > 0 && N == L / 4) {
43 resize(L / 2);
44 System.out.println("resize 1/2");
45 }
46 return max;
47 }
48
49 public Key delMax(int d) {
50 if (N == 0) {
51 System.out.println("none!");
52 }
53 Key max = pq[1];
54 exch(1, N--);
55 pq[N + 1] = null;
56 sinkM(1, d);
57 if (N > 0 && N == L / 4) {
58 resize(L / 2);
59 System.out.println("resize 1/2");
60 }
61 return max;
62 }
63
64 private void swim(int k) {// 二叉堆
65 while (k > 1 && less(k / 2, k)) {
66 exch(k / 2, k);
67 k = k / 2;
68 }
69 }
70
71 private void swim(int k, int d) {// d叉堆:(k+d-2)/d为d叉堆第k个节点的父节点
72 while (k > 1 && less((k + d - 2) / d, k)) {
73 exch((k + d - 2) / d, k);
74 k = (k + d - 2) / d;
75 }
76 }
77
78 private void sink(int k) {// 二叉堆
79 while (2 * k <= N) {
80 int j = 2 * k;
81 if (j < N && less(j, j + 1)) {
82 j++;
83 }
84 if (!less(k, j)) {
85 break;
86 }
87 exch(k, j);
88 k = j;
89 }
90 }
91
92 private void sinkM(int k, int d) {// d叉堆
93 while (d * k - (d - 2) <= N) {// d叉堆k节点的第一个子节点
94 int j = d * k - (d - 2);
95 int flag = k;
96 while (j <= N && j <= d * k + 1) {
97 if (less(flag, j)) {
98 flag = j;
99 }
100 j++;
101 }
102 if (flag == k) {// flag没有改变
103 break;
104 }
105 exch(k, flag);
106 k = flag;
107 }
108 }
109
110 private void resize(int n) {
111 Key[] temp = (Key[]) new Comparable[n + 1];
112 for (int i = 1; i <= N; i++) {
113 temp[i] = pq[i];
114 }
115 pq = temp;
116 L = n;
117 }
118
119 private void exch(int i, int j) {
120 Key temp = pq[i];
121 pq[i] = pq[j];
122 pq[j] = temp;
123 }
124
125 private boolean less(int i, int j) {
126 return pq[i].compareTo(pq[j]) < 0;
127 }
128
129 public void sort(Comparable[] a) {//堆排序
130 int n=N;
131 for(int k=n/2;k>=1;k--) {
132 sink(k,n);
133 }
134 while(n>1) {
135 exch(1,n--);
136 sink(1,n);
137 }
138 }
139
140 private void sink(int k, int n) {//二叉树 从k到n排序
141 while (2 * k <= n) {
142 int j = 2 * k;
143 if (j < n && less(j, j + 1)) {
144 j++;
145 }
146 if (!less(k, j)) {
147 break;
148 }
149 exch(k, j);
150 k = j;
151 }
152 }
153
154 public static void main(String[] args) {
155 MaxPQ mpq = new MaxPQ<>(3);
156 mpq.insert(1);
157 mpq.insert(2);
158 mpq.insert(3);
159 mpq.insert(4);
160 mpq.insert(5);
161 mpq.insert(6);
162 mpq.insert(7);
163 mpq.insert(8);
164 mpq.insert(9);
165 mpq.insert(10);
166 mpq.insert(11);
167 mpq.sort(mpq.pq);
168 for(int i=1;i<=N;i++) {
169 System.out.println(mpq.pq[i]);
170 }
171 /*for (int i = 1; i <= 13; i++) {
172 System.out.println(mpq.delMax());
173 }*/
174 }
175
176 }