图的连通性算法-Kosaraju

Kosaraju算法

适用范围及时间复杂度

线性时间算法，找一个有向图的强连通分量（分量中所有点都是连通的）。

算法原理

首先有一个定义，名曰反图。何为反图？即将图中所有边反向操作。

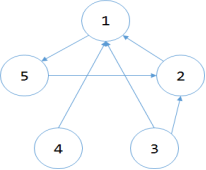
上图样例即为一对反图。在整副图中,有三个强连通分量,即:1 2 5,3,4.如果把这副图所有边反向后,得到的同样是三个强连通分量。

即原图和反图的强连通分量的数量和每个强连通分量中的元素都是一样的,只是顺序不一样。

核心思想

先对原图进行DFS（深度优先搜索），保存每个节点退出DFS的次序，即后序数。

然后再用后序数最大点为顶点作为始点，对反图进行DFS。如此反复，直到访问完反图的所有节点为止。

把每一次对反图进行DFS所产生的顶点进行标号，即这些顶点为同一个强分支。

代码实现

这里以int cnt表示分支标号，每个点所属的分支标号用num[MAXN]记录。

用vect[MAXN]来存放后序。

    for(int i=n-1;i>=0;i--){
        if(!num[vect[i]]){//如果这个节点还没有被标号 
            cnt++;//创建新的分支 
            rdfs(vect[i]);//通过深搜把该分支节点标号 
        }
    }

void rdfs(int u){
    if(num[u]){
        return;
    }
    num[u]=cnt;
    for(int i=0;i<gt[u].size();i++){
        rdfs(gt[u][i]);
    }
}