Problem Description
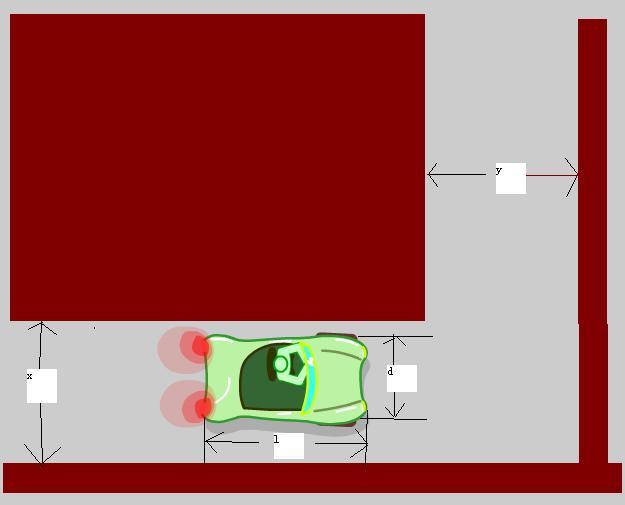
Mr. West bought a new car! So he is travelling around the city. One day he comes to a vertical corner. The street he is currently in has a width x, the street he wants to turn to has a width y. The car has a length l and a width d. Can Mr. West go across the corner?
Input
Every line has four real numbers, x, y, l and w.
Proceed to the end of file.
Output
If he can go across the corner, print "yes". Print "no" otherwise.
Sample Input
10 6 13.5 4 10 6 14.5 4
Sample Output
yes
no
Source
摘自大牛的解题报告:
题意:给定一个直角弯道的两条道路的宽度,然后再给出汽车的长度与宽度,问汽车能否通过该弯道?
如下图:

要使汽车能转过此弯道,那么就是汽车的左边尽量贴着那个直角点,而汽车的右下后方的点尽量贴着最下面的边。
我们以O点为原点建立直角坐标系,我们可以根据角a给出P点横坐标的函数F(a)
那么很容易得到:

其中有条件: ,可以很容易证明
,可以很容易证明 是一个单峰函数,所以接下来就是三分了,如果
是一个单峰函数,所以接下来就是三分了,如果 的最大值小于等于
的最大值小于等于
 ,可以很容易证明
,可以很容易证明 是一个单峰函数,所以接下来就是三分了,如果
是一个单峰函数,所以接下来就是三分了,如果 的最大值小于等于
的最大值小于等于y,那么就能通过此直角弯道,否则就通不过。
在三分的时候,写成这样
mid1=(low+high)/2; mid2=(mid1+high)/2;
一直WA,直到写成下面这样才AC,
double mid1=(2*low+high)/3;
double mid2=(low+2*high)/3;

1 #pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<cmath> 6 #include<math.h> 7 #include<algorithm> 8 #include<queue> 9 #include<set> 10 #include<bitset> 11 #include<map> 12 #include<vector> 13 #include<stdlib.h> 14 #include <stack> 15 using namespace std; 16 int dirx[]={0,0,-1,1}; 17 int diry[]={-1,1,0,0}; 18 #define PI acos(-1.0) 19 #define max(a,b) (a) > (b) ? (a) : (b) 20 #define min(a,b) (a) < (b) ? (a) : (b) 21 #define ll long long 22 #define eps 1e-10 23 #define MOD 1000000007 24 #define N 1000000 25 #define inf 1<<26 26 27 double x,y,l,w; 28 double equ(double t) 29 { 30 return l*cos(t)+(w-x*cos(t))/sin(t); 31 } 32 int main() 33 { 34 35 while(scanf("%lf%lf%lf%lf",&x,&y,&l,&w)==4){ 36 double low=0; 37 double high=PI/2.0; 38 // double mid1=(low+high)/2; 39 //double mid2; 40 double sum1; 41 double sum2; 42 while(high-low>eps){ 43 double mid1=(2*low+high)/3;//要这样找mid 44 double mid2=(low+2*high)/3;//要这样找mid 45 sum1=equ(mid1); 46 sum2=equ(mid2); 47 if(sum1<sum2){ 48 low=mid1; 49 } 50 else{ 51 high=mid2; 52 } 53 54 } 55 if(equ(low)<=y){ 56 printf("yes "); 57 } 58 else{ 59 printf("no "); 60 } 61 62 } 63 return 0; 64 }
