插入排序

算法思想

• 将数据分为两部分:有序表,无序表;开始时有序表为空,无序表中全部是待排序数据,依次从无序表中取出待
  排序元素插入到有序表中的合适位置,使有序表中的元素保持有序,直到无序表为空,表示排序完成。

  例如:对数组使用插入排序
  
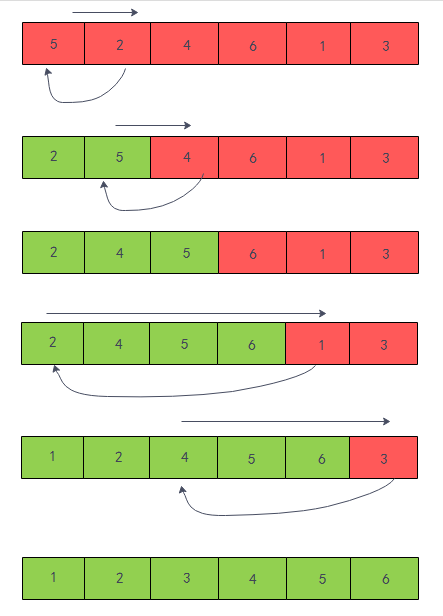
  红色部分表示无序表,绿色部分表示有序表,直线箭头表示挪动元素以留出空间,以便元素的插入,
  弧形箭头表示当前待排序元素的插入位置;

代码实现

• 使用C语言实现插入排序:

  bool InsertSort(int * pUnSortAry, int nArySize)
  {
    if (pUnSortAry == nullptr || nArySize <= 0)
    {
      return false;
    }
  
    for (int iIndex = 1; iIndex < nArySize; iIndex++)
    {
      int nCurrentValue = pUnSortAry[iIndex];
      int jIndex = iIndex - 1;
      for (; jIndex >= 0 && nCurrentValue < pUnSortAry[jIndex]; jIndex--)
      {
        pUnSortAry[jIndex + 1] = pUnSortAry[jIndex];
      }
      pUnSortAry[jIndex + 1] = nCurrentValue;
    }
  
    return true;
  }
  

  测试代码如下:

  void printAry(const int * pAry, int nSize)
  {
    for (int iIndex = 0; iIndex < nSize; iIndex++)
    {
      printf("%d ", pAry[iIndex]);
    }
    printf("
  ");
  }
  
  
  
  int main()
  {
    srand(time(NULL));
    int nAry[20];
    for (int iIndex = 0; iIndex < 10; iIndex++)
    {
      memset(nAry, 0, sizeof(nAry)/sizeof(nAry[0]));
      for (int jIndex = 0; jIndex < sizeof(nAry) / sizeof(nAry[0]); jIndex++)
      {
        nAry[jIndex] = rand() % 150;
      }
      printf("
  排序前:");
      printAry(nAry, sizeof(nAry) / sizeof(nAry[0]));
      InsertSort(nAry, sizeof(nAry) / sizeof(nAry[0]));
      printf("排序后:");
      printAry(nAry, sizeof(nAry) / sizeof(nAry[0]));
    }
  }
  

  结果:
  

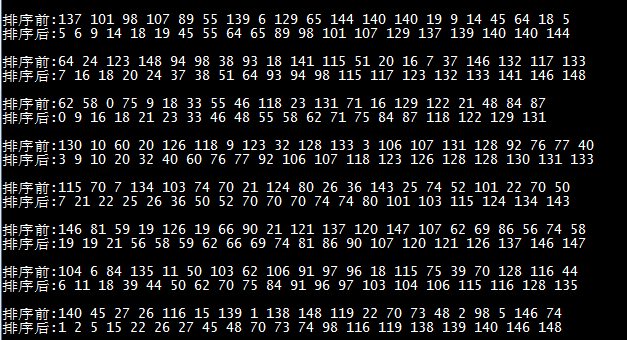
时间复杂度分析

插入排序的核心代码如下:假设数组大小为n

 for (int iIndex = 1; iIndex < nArySize; iIndex++) //执行n次
 {
    int nCurrentValue = pUnSortAry[iIndex];        //执行n-1次
    int jIndex = iIndex - 1;                       //执行n-1次
    //执行t1+t2+....ti次, i=iIndex;
    for (; jIndex >= 0 && nCurrentValue < pUnSortAry[jIndex]; jIndex--) 
    {
      pUnSortAry[jIndex + 1] = pUnSortAry[jIndex]; //执行t1+t2+....ti-1次
    }
    pUnSortAry[jIndex + 1] = nCurrentValue; //执行n-1次
}

t1,t2,......,tn表示执行第iIndex次循环时,内层for循环执行的次数,那么总的时间复杂度如下:
T(n) = n+3*(n-1)+ 2*(t1+t2+.....+tn) -1;

• 当数组中的所有元素排序前已经处于有序状态时,那么此时内层for循环执行只执行一次判断,所以此时的时间
  复杂度为T(n) = n+4*(n-1) = O(n);

• 当数组中的元素逆序时,此时当外层for循环第iIndex次执行时,内层for循环执行执行的次数:
  t1+t2+......+ti=1+2+3....+n =(1+n)n/2
  此时的时间复杂度T(n)=n+3(n-1)+(1+n)*n-1=O(n^2)

稳定性

插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然，刚开始这个有序的小序列只有1个
元素，就是第一个元素。比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,
如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的,
那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的
顺序就是排好序后的顺序,所以插入排序是稳定的.