红黑树

性质

红黑树是满足下列性质的二叉树:

1. 树中只有红色的节点和黑色的节点

2. 根节点是黑色的

3. 外部节点(NIL)都是黑色的
   注意:这里的外部节点指的是这样的节点:
   
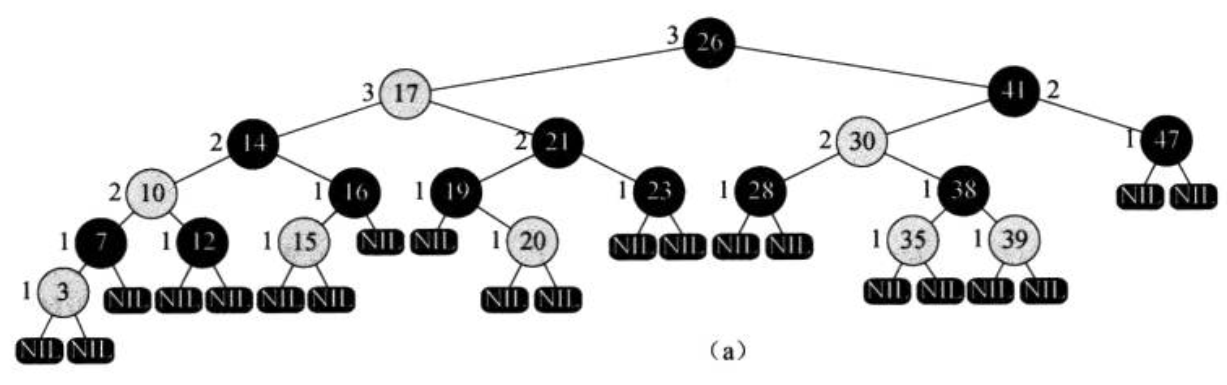
   为了节省空间可以使他们指向同一个外部节点
   
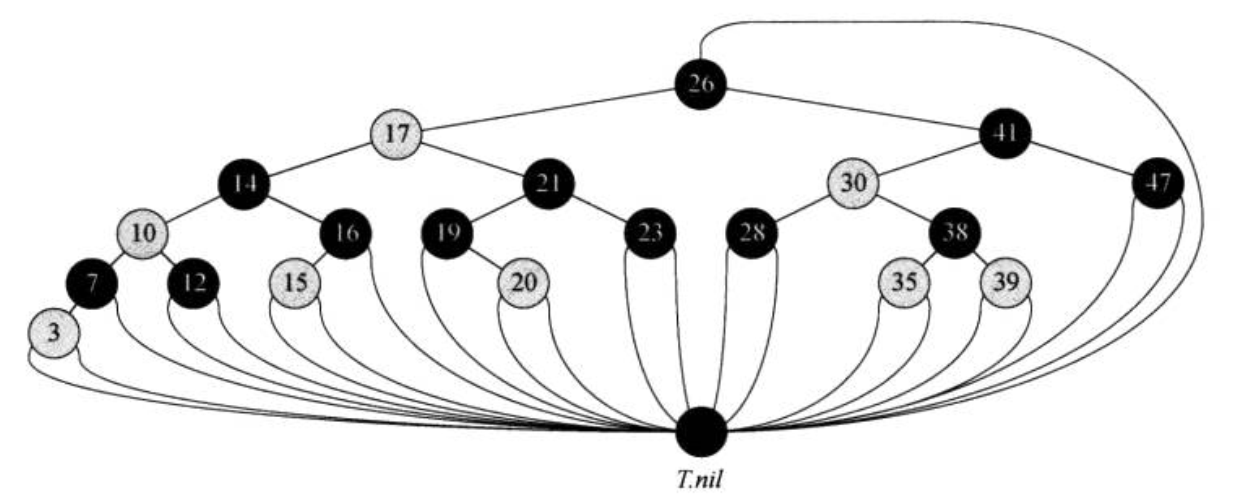
   对于C/C++语言来说可以不设外部节点,如果一个节点没有子节点,可以将其节点的指针域置为空,可以视空节点
   为外部节点

4. 如果一个节点是红色的,那么它的左右孩子节点必须是黑色的

5. 对于每个节点,从该节点到其所有后代外部节点的简单路径上,所经过黑色节点的个数相同,也称为"黑高"

根据上述性质,使用C++语言定义树节点如下:

enum RB_COLOR
{
  RED,
  BLACK
};

template<typename T>
struct tagRBNode
{
  struct tagRBNode<T> * m_pLeft;  //指向左孩子
  struct tagRBNode<T> * m_pRight; //指向右孩子
  struct tagRBNode<T> * m_pParent;//指向父节点
  RB_COLOR m_Color;                //节点颜色
  T m_TDataElemet;                //数据域
  tagRBNode(T & data, RB_COLOR bRed = RED) :
    m_pParent(nullptr),
    m_pLeft(nullptr),
    m_pRight(nullptr),
    m_TDataElemet(data),
    m_Color(bRed)
  {
  }
};

/*定义模版节点类型别名*/
template<typename T>
using RBNode = tagRBNode<T>;

/*定义模版节点指针类型别名*/
template<typename T>
using PRBNode = tagRBNode<T>*;

红黑树类模版定义如下:

template<typename T>
class CRBTree
{
  PRBNode<T> m_Root; //指向根节点
  int m_nNumOfNode;  //记录节点个数
public:
  CRBTree();
  bool Insert(T && data);
  bool Insert(T & data);
  bool Delete(T && data);
  bool Delete(T & data);
private:
  bool LRotate(PRBNode<T> ParentOfPair);
  bool RRotate(PRBNode<T> ParentOfPair);
  bool FixAfterInsert(PRBNode<T> pNewNode);
  PRBNode<T> FindNodeByData(T & data);
  bool ReplaceNode(PRBNode<T> pBeReplaced, PRBNode<T> pReplacer);
  bool FixAfterDelete(PRBNode<T> pAdjustNode, PRBNode<T> pParentOfAdjust);
};

为了让代码中的操作开起来更直观可读,定义了如下的宏:

#define IS_LEFT_CHID(parent,child) ((((parent)->m_pLeft) == (child)) ? true:false)
#define IS_EMPTY(pointer) (((pointer) == nullptr)?true:false)
#define SET_COLOR(pointer,color)                            
do                                                          
{                                                           
  if ((pointer) != nullptr)                                 
  {                                                         
    (pointer)->m_Color = color;                             
  }                                                         
}                                                           
while(0)

#define GET_COLOR(pointer)((pointer)->m_Color)

#define SET_RED_COLOR(pointer)                              
do                                                          
{                                                           
  if((pointer) != nullptr)                                  
  {                                                         
    (pointer)->m_Color = RED;                               
  }                                                         
} while (0)   

#define SET_BLACK_COLOR(pointer)                            
do                                                          
{                                                           
  if((pointer) != nullptr)                                  
  {                                                         
    (pointer)->m_Color = BLACK;                             
  }                                                         
} while (0)

#define IS_RED_COLOR(pointer)     ((((pointer)->m_Color) == RED) ?true:false)
#define IS_BLACK_COLOR(pointer)   ((((pointer)->m_Color) == BLACK) ?true:false)


#define SET_PARENT(parent, child)                           
if(child != nullptr)                                        
{                                                           
  child->m_pParent = parent;                                
}


#define SET_LEFT_CHILD(parent,child)                        
do                                                          
{                                                           
  parent->m_pLeft = child;                                  
  SET_PARENT(parent,child)                                  
}                                                           
while(0)  


#define SET_RIGHT_CHILD(parent,child)                       
do                                                          
{                                                           
  parent->m_pRight = child;                                 
  SET_PARENT(parent,child)                                  
}                                                           
while(0)

#define LINK_GRANDFATHER_GRANDSON(parent,grandson)            
do                                                            
{                                                             
  if(parent->m_pParent == nullptr)                            
  {                                                           
    m_Root = grandson;                                        
  }else if (parent->m_pParent->m_pLeft == parent)             
  {                                                           
    parent->m_pParent->m_pLeft = grandson;                    
  }                                                           
  else                                                        
  {                                                           
    parent->m_pParent->m_pRight = grandson;                   
  }                                                           
  grandson->m_pParent = parent->m_pParent;                    
}while(0)

旋转节点

S1,S2,S3指代整个子树,X表示待旋转节点的父节点

• 左旋
  旋转前:
  
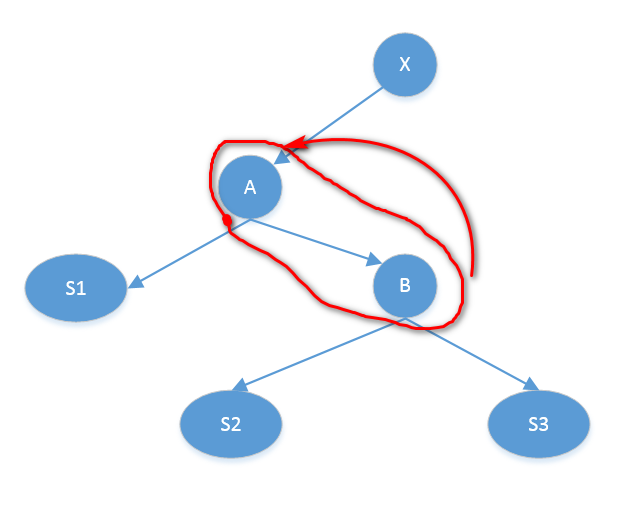
  旋转后:
  

 
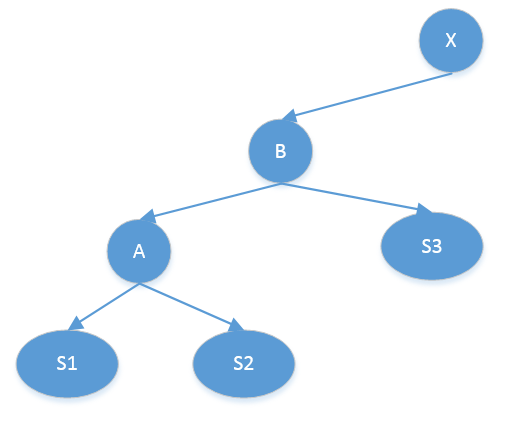
左旋代码实现:

/************************************************************************
// 函数名称: CRBTree<T>::LRotate
// 访问权限: private 
// 函数功能: 对一对节点进行左旋
// 返回值:   bool:成功返回true,失败返回false
// 参数:     PRBNode<T> ParentOfPair:待左旋的父节点
// 注意:     ParentOfPair必须要有右孩子
************************************************************************/
template<typename T>
bool CRBTree<T>::LRotate(PRBNode<T> ParentOfPair)
{
  PRBNode<T>  pRChildOfParent = ParentOfPair->m_pRight;
  if (ParentOfPair == nullptr || pRChildOfParent == nullptr)
  {
    return false;
  }

  LINK_GRANDFATHER_GRANDSON(ParentOfPair, pRChildOfParent);

  SET_RIGHT_CHILD(ParentOfPair, pRChildOfParent->m_pLeft);
  SET_PARENT(ParentOfPair, pRChildOfParent->m_pLeft);

  SET_LEFT_CHILD(pRChildOfParent, ParentOfPair);
  SET_PARENT(pRChildOfParent, ParentOfPair);
  return true;
}

• 右旋
  旋转前:
  
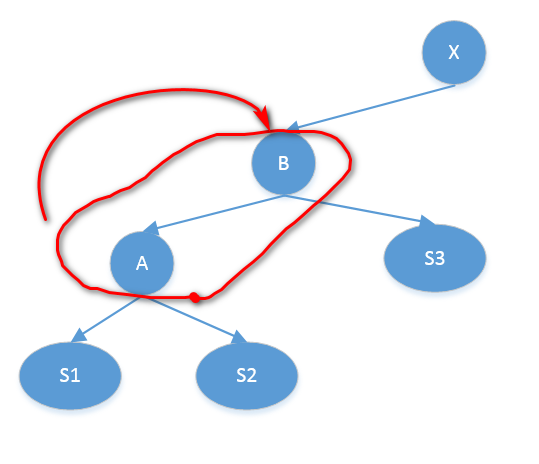
  旋转后:
  

 
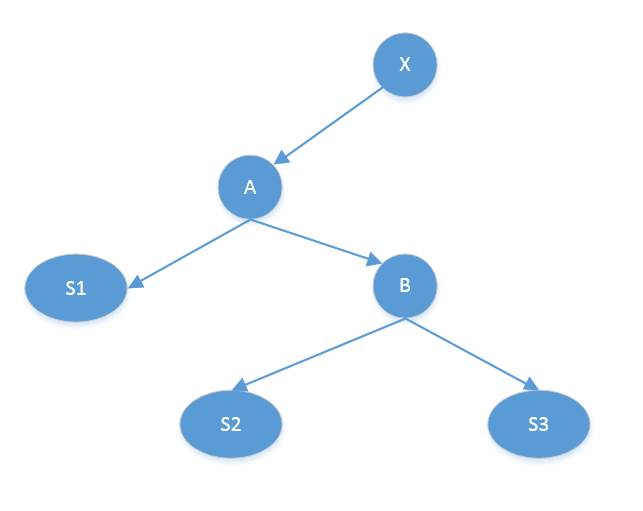
右旋代码实现:

/************************************************************************
// 函数名称: CRBTree<T>::RRotate
// 访问权限: private 
// 函数功能: 对一对节点进行右旋
// 返回值:   bool:成功返回true,失败返回false
// 参数:     PRBNode<T> ParentOfPair:待右旋的父节点
// 注意:     ParentOfPair必须要有左孩子
************************************************************************/
template<typename T>
bool CRBTree<T>::RRotate(PRBNode<T> ParentOfPair)
{
  PRBNode<T> pLChildOfParent = ParentOfPair->m_pLeft;
  if (ParentOfPair == nullptr || pLChildOfParent == nullptr)
  {
    return false;
  }


  LINK_GRANDFATHER_GRANDSON(ParentOfPair, pLChildOfParent);

  SET_LEFT_CHILD(ParentOfPair, pLChildOfParent->m_pRight);
  SET_PARENT(ParentOfPair, pLChildOfParent->m_pRight);

  SET_RIGHT_CHILD(pLChildOfParent, ParentOfPair);
  SET_PARENT(pLChildOfParent, ParentOfPair);
  return true;
}

插入节点

如果红黑树为空则直接插入即可,如果红黑树不为空,则需要使用类似"二分查找"的方式来找到合适的插入位置,
插入前节点需要着色,一般都是设置为红色,因为一个非空红黑树从根节点到任意叶节点的黑高是相同的,所以插入
一个红色的节点不会影响所在路径的黑高(性质5),可能会造成与其父节点都是红色(性质4);但是如果讲新节点着
黑色插入,那么一定会影响所在路径的黑高,则每次插入都必须做出调整

 
下面给出插入的实现代码:

/************************************************************************
// 函数名称: CRBTree<T>::Insert
// 访问权限: public 
// 函数功能: 插入一个值
// 返回值:   bool:成功返回true,失败返回false
// 参数:     T & data:要插入的值
// 注意:     1.传入的参数data必须是一个左值
            2.如果data已经存在则返回失败
************************************************************************/
template<typename T>
bool CRBTree<T>::Insert(T & data)
{
  /*先查找插入位置*/
  PRBNode<T> pParentOfInsertLoc = m_Root;
  PRBNode<T> pSearchLoc = m_Root;
  while (pSearchLoc != nullptr)
  {
    pParentOfInsertLoc = pSearchLoc;
    if (pSearchLoc->m_TDataElemet < data)
    {
      pSearchLoc = pSearchLoc->m_pRight;
    }
    else if (pSearchLoc->m_TDataElemet > data)
    {
      pSearchLoc = pSearchLoc->m_pLeft;
    }
    else
    {
      /*带插入的元素已经存在*/
      return false;
    }
  }

  PRBNode<T> pNewNode = new RBNode<T>(data);
  if (pParentOfInsertLoc == nullptr)
  {
    /*树为空,则直接插入*/
    m_Root = pNewNode;
  }
  else if(pParentOfInsertLoc->m_TDataElemet > data)
  {
    SET_LEFT_CHILD(pParentOfInsertLoc, pNewNode);
    SET_PARENT(pParentOfInsertLoc, pNewNode);
  }
  else
  {
    SET_RIGHT_CHILD(pParentOfInsertLoc, pNewNode);
    SET_PARENT(pParentOfInsertLoc, pNewNode);
  }

  m_nNumOfNode++;
  FixAfterInsert(pNewNode);
  return true;
}


/************************************************************************
// 函数名称: CRBTree<T>::Insert
// 访问权限: public 
// 函数功能: 插入一个值
// 返回值:   bool:成功返回true,失败返回false
// 参数:     T & & data:节点值
// 注意:     1.传入的参数data必须是一个右值
            2.如果data已经存在则返回失败
************************************************************************/
template<typename T>
bool CRBTree<T>::Insert(T && data)
{
  return Insert(data);
}

因为每次插入的新节点的颜色都是红色,如果是一颗空树插入根节点后,会破坏性质2;如果不是空树,插入后可能破
坏性质4;也有可能不破坏性质4,如果插入后新节点的父节点为黑色;所以插入新节点后要维持红黑树的性质,则从
维护这两个性质开始:

1. 如果新节点的父节点是其祖父节点左孩子
   Case0:向空树插入根节点,或者调整时根节点被置为红色,则直接将根节点置为黑色
   
    
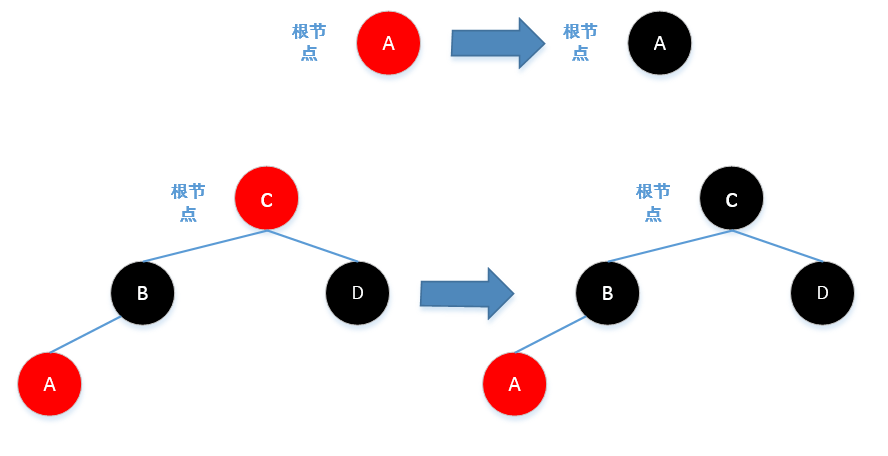
   Case1:插入后,待调整节点的父节点为红色,并且待调整节点的叔节点也为红色,此时待调整节点的祖父节点必定是
   黑色的,那么将父节点和叔节点置为黑色,将祖父节点置为红色;但是祖父节点的父节点有可能红色的,所以
   调整位置要移动到祖父节点,继续向上调整,可以看出维持红黑树性质的算法中肯定有一个循环
   
    
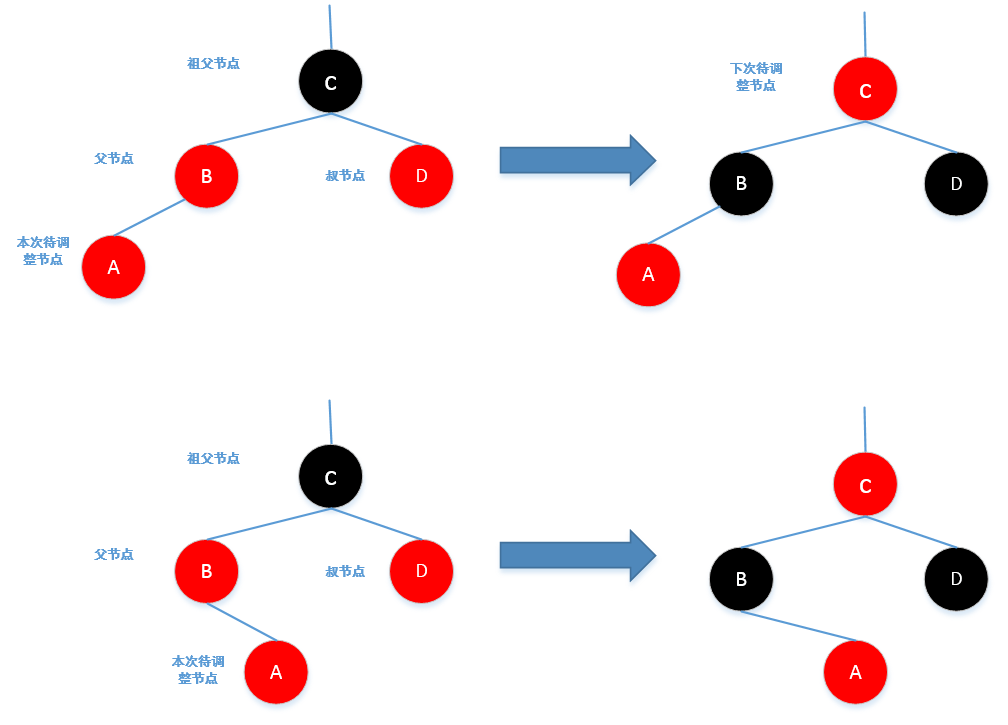
   Case2:插入后,待调整节点的父节点为红色,并且待调整节点的叔节点为黑色(无叔节点也视为黑色),并且待调整节
   点是其父节点的右孩子,那么此时需要对待调整节点和其父节点进行一次左旋
   
    
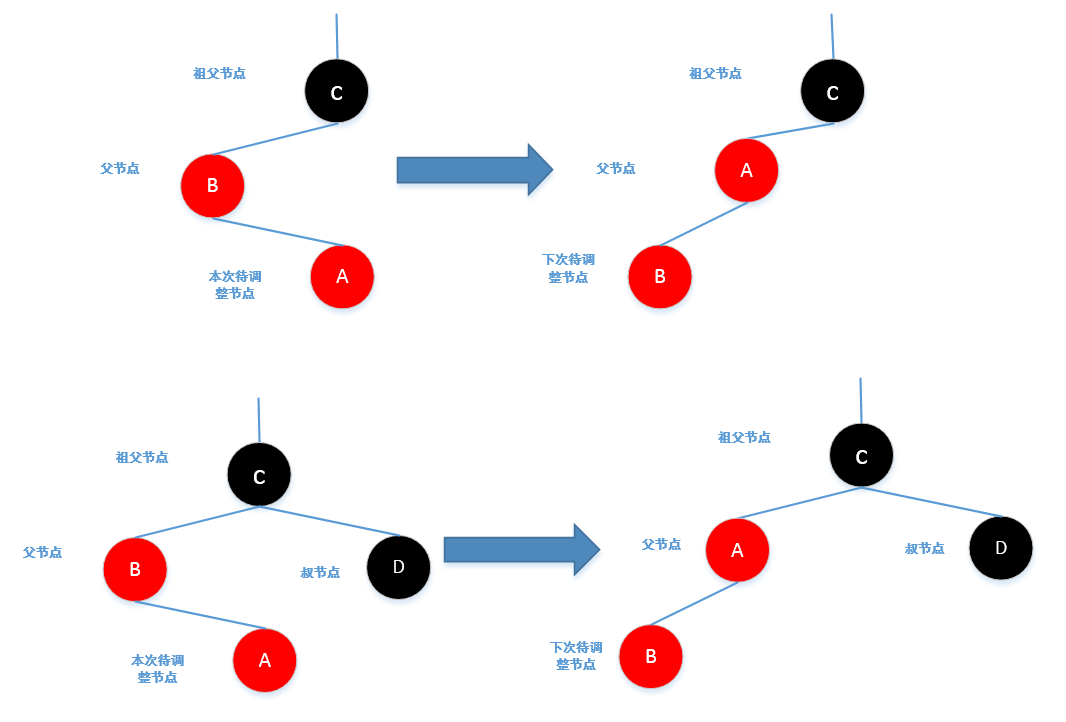
   Case3:插入后(或者经过Case2调整后),待调整节点的父节点为红色,并且待调整节点的叔节点为黑色(无叔节点也
   视为黑色),此时将待调整节点的父节点置为黑色,将待调整节点的祖父节点置为红色,并对父节点和祖父节
   点进行一次右旋
   
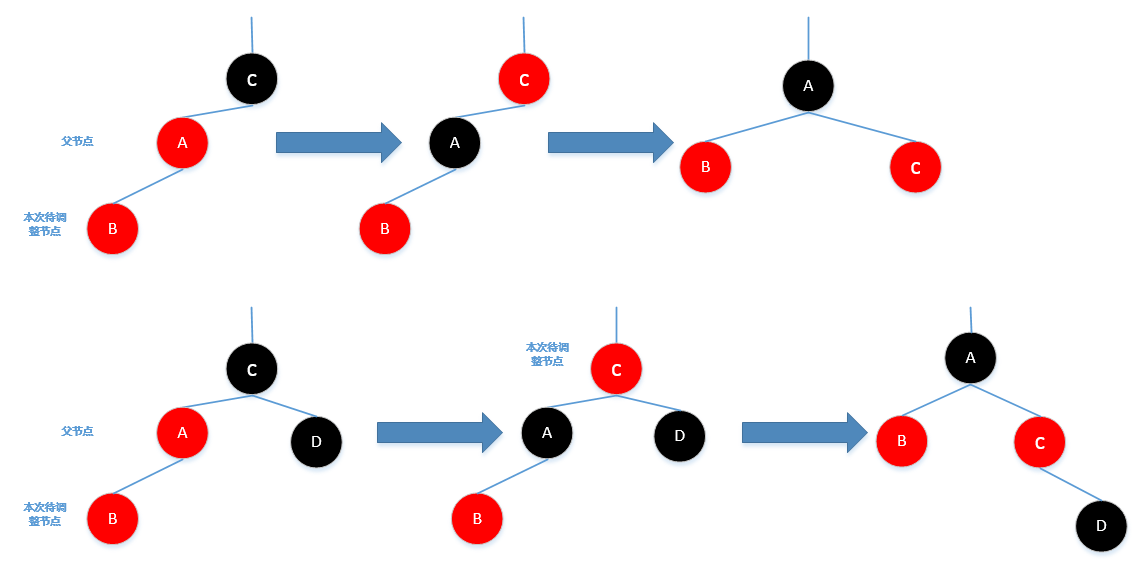
2. 如果新节点的父节点是其祖父节点右孩子
    
   Case2:插入后,待调整节点的父节点为红色,并且待调整节点的叔节点为黑色(无叔节点也视为黑色),并且待调整节
   点是其父节点的左孩子,那么此时需要对待调整节点和其父节点进行一次右旋
   
    
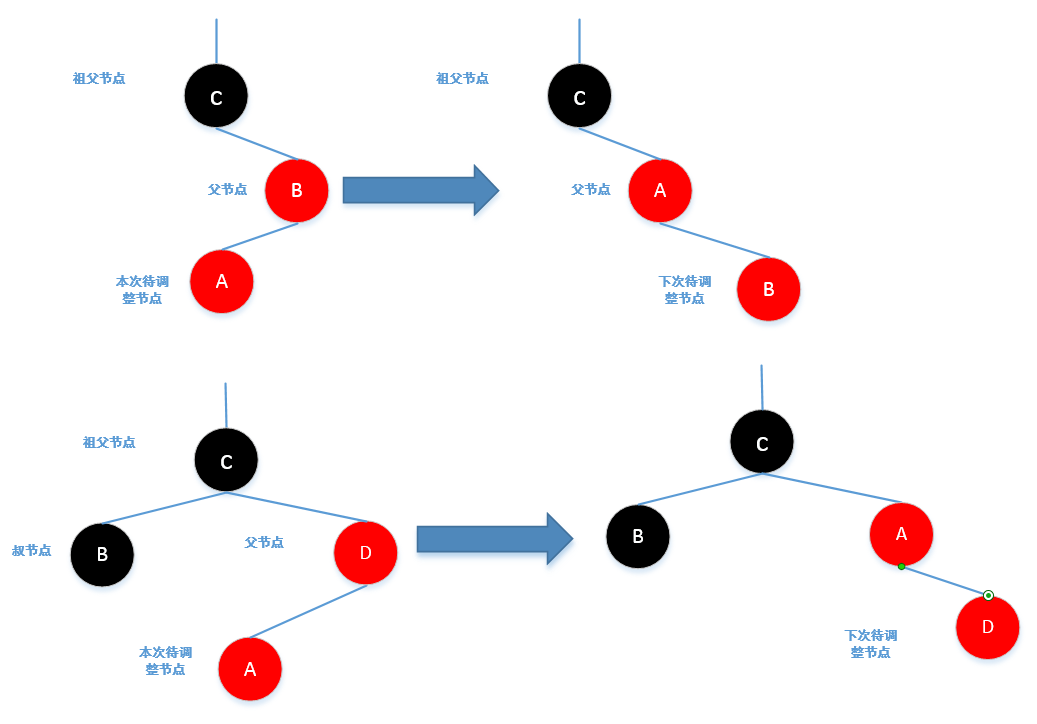
   Case3:插入后(或者经过Case2调整后),待调整节点的父节点为红色,并且待调整节点的叔节点为黑色(无叔节点也
   视为黑色),此时将待调整节点的父节点置为黑色,将待调整节点的祖父节点置为红色,并对父节点和祖父节
   点进行一次左旋
   

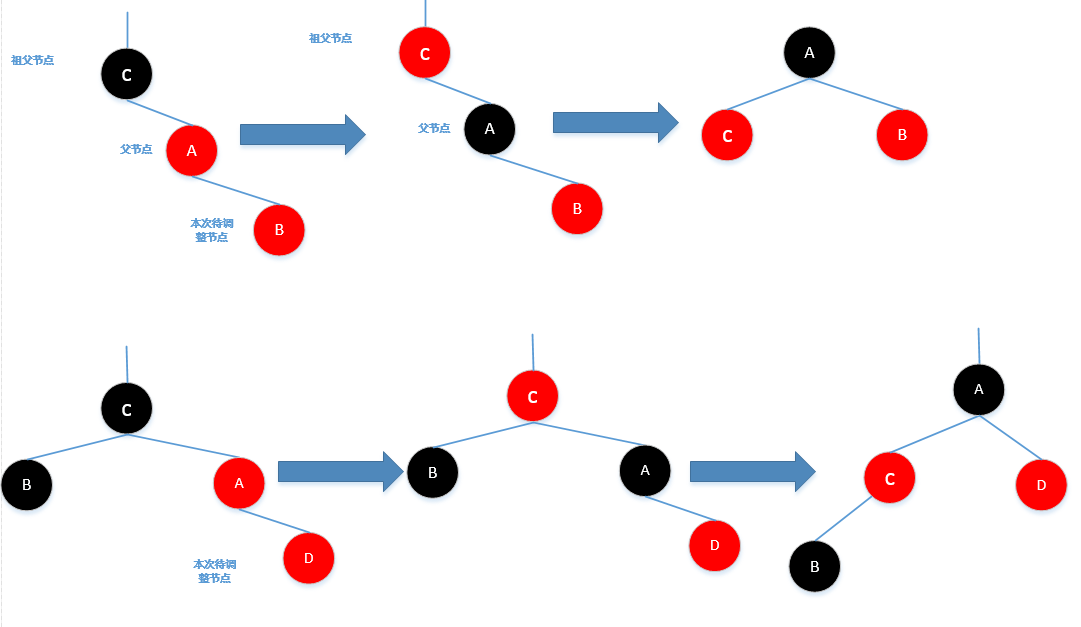
根据上面的几种情形得出下面是插入后维持红黑树性质的代码:

/************************************************************************
// 函数名称: CRBTree<T>::FixAfterInsert
// 访问权限: private
// 函数功能: 插入新节点后调整以维护红黑树性质
// 返回值:   bool
// 参数:     PRBNode<T> pNewNode:新插入的节点
// 注意:
************************************************************************/
template<typename T>
bool CRBTree<T>::FixAfterInsert(PRBNode<T> pNewNode)
{
  PRBNode<T> pParent = nullptr;
  PRBNode<T> pUncle = nullptr;
  PRBNode<T> pGrand = nullptr;
  PRBNode<T> pAdjust = pNewNode;
  while ((pParent = pAdjust->m_pParent) && IS_RED_COLOR(pParent))
  {
    pGrand = pParent->m_pParent;
    if (IS_LEFT_CHID(pGrand, pParent))
    {
      pUncle = pGrand->m_pRight;
      if (pUncle != nullptr && IS_RED_COLOR(pUncle))
      {
        /*Case1:待调整节点的叔节点为红色,那么祖父节点必定时黑色的,则将待调整节点父节点和叔节点置为
                置为黑色,将祖父节点置为红色,并将待调整节点设置为祖父节点
        */
        SET_BLACK_COLOR(pParent);
        SET_BLACK_COLOR(pUncle);
        SET_RED_COLOR(pGrand);
        pAdjust = pGrand;
        continue;
      }
      else
      {
        /*叔节点此时一定是黑色(不存在也视为黑色)*/
        if (!IS_LEFT_CHID(pParent, pAdjust))
        {
          /*case2:待调整节点是其父节点的右孩子,则进行一次左旋,并重置待调整位置*/
          pAdjust = pParent;
          LRotate(pParent);
          pParent = pAdjust->m_pParent;
        }

        /*Case3:此时待调整节点为父节点的左孩子,将祖父节点置为红色,然后对祖父节点执行一次右旋,
                 调整就结束了*/
        SET_BLACK_COLOR(pParent);
        SET_RED_COLOR(pGrand);
        RRotate(pGrand);
      }
    }
    else
    {
      pUncle = pGrand->m_pLeft;
      if (pUncle != nullptr && IS_RED_COLOR(pUncle))
      {
        /*Case1:叔节点为红色*/
        SET_BLACK_COLOR(pUncle);
        SET_BLACK_COLOR(pParent);
        SET_RED_COLOR(pGrand);
        pAdjust = pGrand;
        continue;
      }
      else
      {
        /*此时叔节点为黑色(不存在也视为黑色)*/
        if (IS_LEFT_CHID(pParent, pAdjust))
        {
          /*Case2:待调整节点是其父节点的左孩子,则对父节点进行右旋*/
          pAdjust = pParent;
          RRotate(pParent);
          pParent = pAdjust->m_pParent;
        }

        /*Case3:此时待调整节点为父节点的右孩子,将父节点置为黑色,祖父节点置为红色,
                在对祖父节点进行一次左旋即可结束调整*/
        SET_BLACK_COLOR(pParent);
        SET_RED_COLOR(pGrand);
        LRotate(pGrand);
      }
    }
  }
  SET_BLACK_COLOR(m_Root);
  return true;
}

插入节点时间复杂度分析

插入前寻找插入位置的代码复杂度与红黑树的高度有关,所以需要找出节点总个数n与树高度h的关系;
设任意节点x的黑高为hb(x)(不小于0),先证明任意节点x的至少含有2^hb(x)-1个内部节点:
当hb(x)=0时,节点x的是外部节点或者叶节点;x为外部节点时,其内部节点的个数为0,x为叶节点时,x含有一个内
部节点就是它自己;则hb(x)=0时,至少含有2^hb(x)-1成立;
 
当节点x的hb(x)!=0时,也即hb(x)>0时,假设其左右孩子都存在,当孩子节点为红色时,孩子节点的黑高也为hb(x);
当孩子节点为黑色时,孩子节点的高度为hb(x)-1;不管节点x的孩子节点是红的还是黑的,那么孩子节点的黑高至少
是hb(x)-1,那么节点x含有外部节点的个数至少为(包括x自己):2^(hb(x)-1)-1+2^(hb(x)-1)-1+1,简化后即
为:2^hb(x)-1;这里有子树黑高hb(x)-1推出其父节点黑高为hb(x)时至少含2^hb(x)-1内部节点,所以有数学
归纳法可以证明任意节点x的至少含有2^hb(x)-1个内部节点是正确的
 
假设红黑树的高度为h节点总数为n,由红黑树的性质4可以推出从根节点到任意外部节点的简单路径上,黑节点的个
数至少为h/2,则说明高度为h的红黑树的黑高至少为h/2,则说明根节点至少含有2^(h/2)-1个内部节点,可以推出:
2^(h/2)-1<n,可推得2^(h/2)<n+1,不等式两边同时对2取对数后得:h/2<lg(n+1),最终可以得到高度h满足:
h<2lg(n+1),也就是说含n个节点的红黑树,高度至多为2lg(n+1)
 
红黑树也是一种二叉树,那么其查找节点的时间复杂度T(n)=O(2lg(n+1))=O(lgn),所以红黑树中插入节点前查找
代码时间复杂度为O(n);插入后为了维持红黑树的性质,需要沿着插入位置向根节点调整,如果违反了性质1,那么
重新着色和调整位置向上移动两层,所以循环最多执行lg(n+1)次;另外每次循环中旋转的次数不会超过两次,只要
进入了Case2和Case3执行两次旋转后,本次循环就结束了,所以维持插入后维持红黑树性质的代码时间复杂度为
O(lgn),所以插入总的时间复杂度为O(lgn)

删除节点

这里为了方便描述,称待删除节点为D,其左孩子为DL,右孩子为DR,其父节点为DP;用于替换待删除节点的节点称为X,
它的左孩子称为XL,右孩子称为XR,其父节点称为XP,红黑树节点的删除和二叉搜索树删除节点类似,分为以下三种
情况:

• 如果待删除的节点无左右孩子,则直接将其删除即可,并修改其父节点对应的孩子指针即可
  
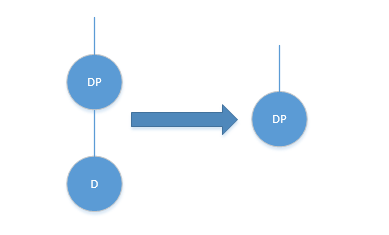
  上图中没有明显的画出D是父节点左孩子还是右孩子,这咩有关系,无论D是父节点左孩子还是右孩子处理方式都
  一样
• 如果待删除节点只有一个孩子,直接用待删除节点的这个孩子来取代待删除节点,并重置相关指针指向即可
  
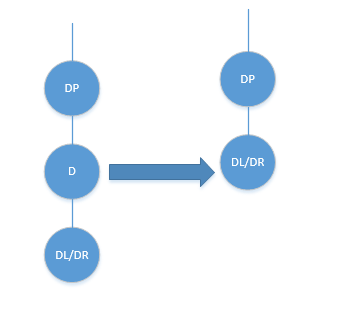
• 如果待删除节点两个孩子都存在,则从其右子树上寻找一个最小的节点来替换待删除节点,并重置相关指针指向即可
  从待删除节点的右子树上找到的这个最小的节点,它一定没有左孩子,只要它有左孩子那么它就不是最小的节点,
  可能会有右孩子
  
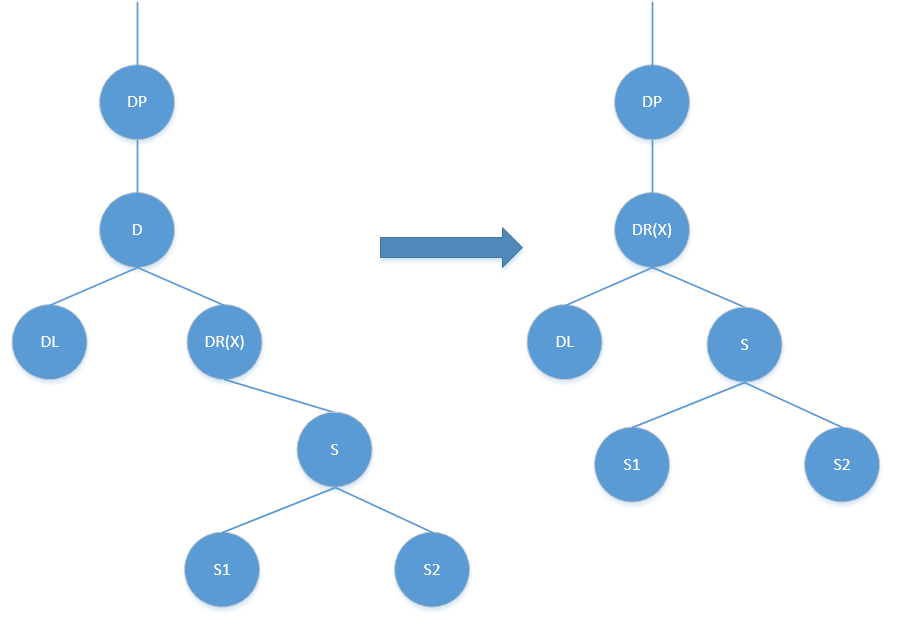
  上图展现一个比较特殊的情况,当待删除节点的右孩子没有左孩子,那么待删除节点的右孩子就是待删除节点右
  子树中节点值最小的节点,除了这种特殊情况外,更多是下图中的情况:
  

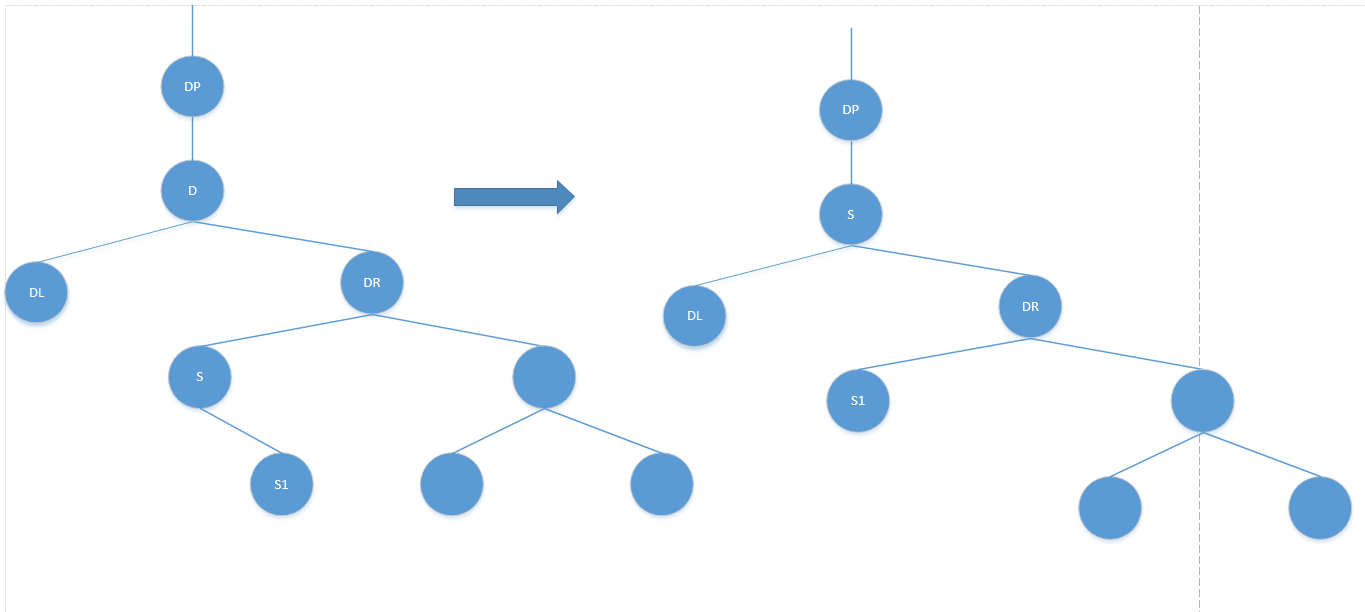
从上面三种情况可以看出节点的替换是一个常用操作,所以将此操作封装为一个成员函数:

/************************************************************************
// 函数名称: CRBTree<T>::ReplaceNode
// 访问权限: private
// 函数功能: 用pReplacer指向的节点替换pBeReplaced指向的节点
// 返回值:   bool
// 参数:     PRBNode<T> pBeReplaced:待替换的节点
// 参数:     PRBNode<T> pReplacer用于替换的节点
// 注意:     pBeReplaced不能为空
************************************************************************/
template<typename T>
bool CRBTree<T>::ReplaceNode(PRBNode<T> pBeReplaced, PRBNode<T> pReplacer)
{
  if (pBeReplaced == nullptr)
  {
    return false;
  }

  if (pBeReplaced == m_Root)
  {
    /*根节点被替换*/
    m_Root = pReplacer;
    SET_PARENT(nullptr, pReplacer);
  }
  else if (IS_LEFT_CHID(pBeReplaced->m_pParent, pBeReplaced))
  {
    SET_LEFT_CHILD(pBeReplaced->m_pParent, pReplacer);
  }
  else
  {
    SET_RIGHT_CHILD(pBeReplaced->m_pParent, pReplacer);
  }
  return true;
}

这个函数主要功能是建立DP(待删除节点的父节点)与X(用于替换的节点)间的父子关系,但是没有重置X与DL,DR
间的关系,如果要在这个函数中也完成X与DL,DR节点关系的建立,整个函数将会变得很复杂;

 
删除一个节点前,必须现在红黑树中寻找这个待删除节点,所以还需要实现一个查找的成员函数:

/************************************************************************
// 函数名称: CRBTree<T>::FindNodeByData
// 访问权限: private
// 函数功能: 查找树中是否存在元素值为data的节点
// 返回值:   返回指向该节点的指针,如果没有该节点则返回空指针
// 参数:     T & data:待查找的元素
// 注意:
************************************************************************/
template<typename T>
PRBNode<T> CRBTree<T>::FindNodeByData(T & data)
{
  PRBNode<T> pSearch = m_Root;
  while (pSearch != nullptr)
  {
    if (data > pSearch->m_TDataElemet)
    {
      pSearch = pSearch->m_pRight;
    }
    else if (data < pSearch->m_TDataElemet)
    {
      pSearch = pSearch->m_pLeft;
    }
    else
    {
      break;
    }
  }
  return pSearch;
}

两个辅助函数已经完成,下面则是删除节点函数的实现:

/************************************************************************
// 函数名称: CRBTree<T>::Delete
// 访问权限: public
// 函数功能: 删除一个节点元素为data的节点
// 返回值:   bool:成功返回true,失败返回false
// 参数:     T &  data:待查找的元素
// 注意:     1.data必须是一个左值,本函数用于支持左值作为参数时调用
************************************************************************/
template<typename T>
bool CRBTree<T>::Delete(T & data)
{
  PRBNode<T> pDelNode = FindNodeByData(data);
  PRBNode<T> pParentOfAdjust = nullptr;
  PRBNode<T> pAdjust = nullptr;

  if (pDelNode == nullptr)
  {
    return false;
  }

  RB_COLOR ColorRecorder = GET_COLOR(pDelNode);

  if (pDelNode->m_pLeft == nullptr)
  {
    /*左子树为空则直接使用右孩子来替换待删除节点*/
    pAdjust = pDelNode->m_pRight;
    pParentOfAdjust = pDelNode->m_pParent;
    ReplaceNode(pDelNode, pDelNode->m_pRight);
  }
  else if (pDelNode->m_pRight == nullptr)
  {
    /*右子树为空则使用待删除节点左孩子来替换待删除节点*/
    pAdjust = pDelNode->m_pLeft;
    pParentOfAdjust = pDelNode->m_pParent;
    ReplaceNode(pDelNode, pDelNode->m_pLeft);
  }
  else
  {
    /*待删除节点左右孩子都存在则从右子树中选择一个节点值最小的节点来替代待删除节点*/
    PRBNode<T> pMinNode = pDelNode->m_pRight;
    while (pMinNode->m_pLeft != nullptr)
    {
      pMinNode = pMinNode->m_pLeft;
    }

    ColorRecorder = GET_COLOR(pMinNode);
    pAdjust = pMinNode->m_pRight;

    pParentOfAdjust = pMinNode;
    if (pMinNode != pDelNode->m_pRight)
    {
      /*最小节点不是待删除节点的右孩子,则先将最小节点从原来的位置上摘出来,最小值节点无左孩子,可能有右孩子,
        将其右孩子和其父节点相互链接*/
      ReplaceNode(pMinNode, pMinNode->m_pRight);
      pParentOfAdjust = pMinNode->m_pParent;
      /*将待删除节点的右孩子置为最小节点的右孩子*/
      SET_RIGHT_CHILD(pMinNode, pDelNode->m_pRight);
      SET_PARENT(pMinNode, pMinNode->m_pRight);
    }
    
    /*用最小节点替换待删除节点*/
    ReplaceNode(pDelNode, pMinNode);
    SET_COLOR(pMinNode, GET_COLOR(pDelNode));

    /*将待删除节点的左孩子置为最小节点的左孩子*/
    SET_LEFT_CHILD(pMinNode, pDelNode->m_pLeft);
    SET_PARENT(pMinNode, pDelNode->m_pLeft);
  }

  
  if (ColorRecorder == BLACK)
  {
    /*被删除的节点是黑色的或者替换节点为黑色时,都会影响节点所在的简单路径上黑节点的个数,所以要调整*/
    FixAfterDelete(pAdjust, pParentOfAdjust);
  }

  m_nNumOfNode--;
  delete pDelNode;
  return true;
}


/************************************************************************
// 函数名称: CRBTree<T>::Delete
// 访问权限: public
// 函数功能: 删除一个节点元素为data的节点
// 返回值:   bool:成功返回true,失败返回false
// 参数:     T & & data:待查找的元素
// 注意:     1.data必须是一个右值,本函数用于支持右值作为参数时调用
************************************************************************/
template<typename T>
bool CRBTree<T>::Delete(T && data)
{
  return Delete(data);
}

 
D被删除后,X坐在D原来的位置并且X的节点颜色被置为D的颜色;那么当X为红色时,用X取代D后不会影响X原来所在
简单路径上黑节点的个数,但是如果X为黑色时,一定会影响X原来所在简单路径上黑节点的个数,这时需要从X移走
前的位置开始向上进行调整,以维持红黑树性质;

1. 当待调整节点为其父节点的左孩子时
   Case1:待调整节点的兄弟节点为红色
   调整方法:交换兄弟节点和其父节点的颜色,并对父节点进行一次左旋,左旋后待调整节点的兄弟节点发生了更
   换,重新记录兄弟节点
   
    
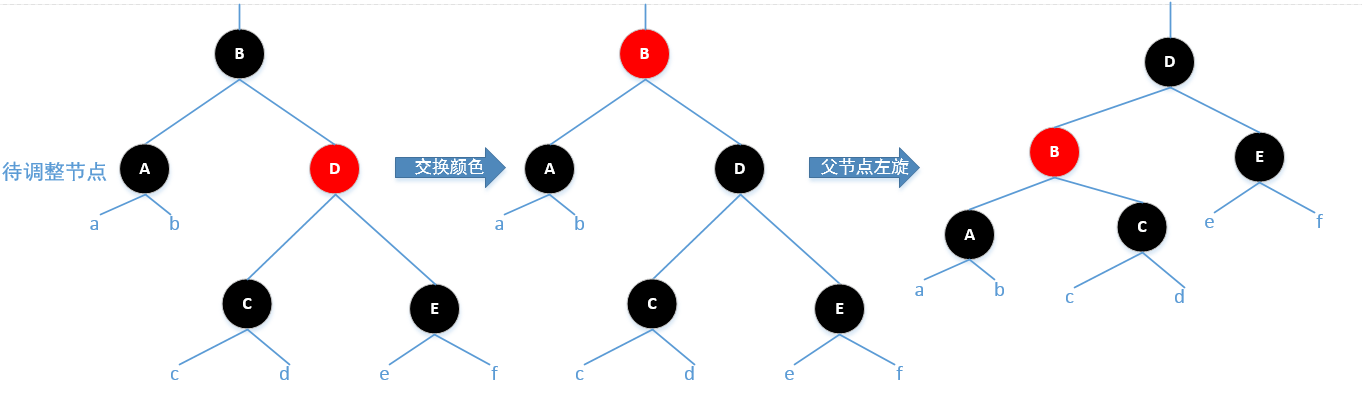
   因为调整前兄弟节点为红色,那么其孩子节点必须是黑色(不存在也视为黑色),经过左旋后,兄弟节点的左孩子
   成为了待调整节点新的兄弟节点,此时Case1就转换为Case2,Case3或者Case4
    
   Case2:待调整节点的兄弟节点是黑色的,父节点颜色任意,并且兄弟节点的左右孩子都为黑色
   调整方法:将兄弟节点置为红色,并将父节点置为下一次的待调整节点
   
    
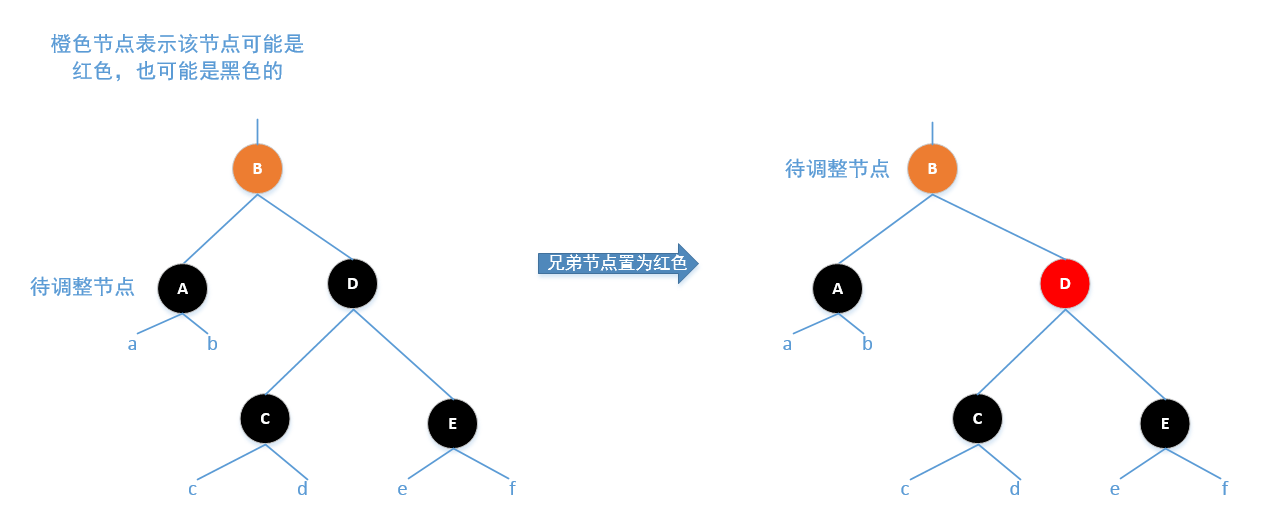
   Case3:待调整节点的兄弟节点为黑色,并且兄弟节点的左孩子为红色,右孩子为黑色
   调整方法:将兄弟节点的颜色和兄弟节点左孩子节点的颜色进行对换,然后对兄弟节点进行右旋
   
    
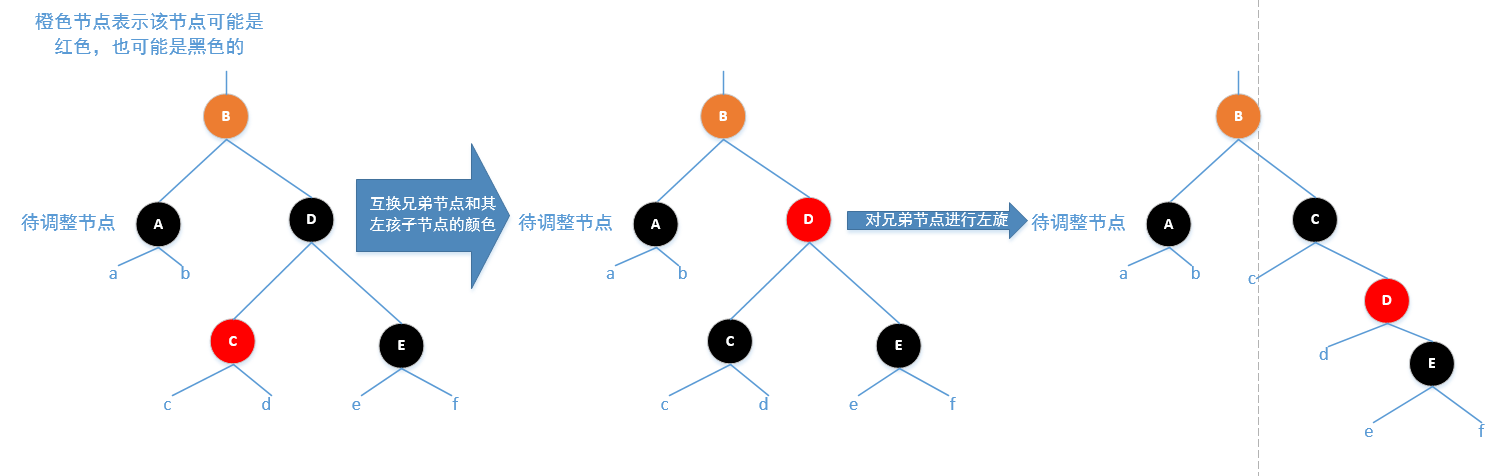
   调整后兄弟节点的右孩子一定是红色的,此时Case3就转换成了Case4
    
   Case4:待调整节点的兄弟节为黑色,并且兄弟节点的右孩子为红色,左孩子颜色任意
   调整方法:将兄弟节点的颜色置为父节点的颜色,然后将父节点置为黑色,将兄弟节点的右孩子置为黑色,然后对
   父节点进行左旋,最后将待调整节点置为根节点,如下图所示:
   
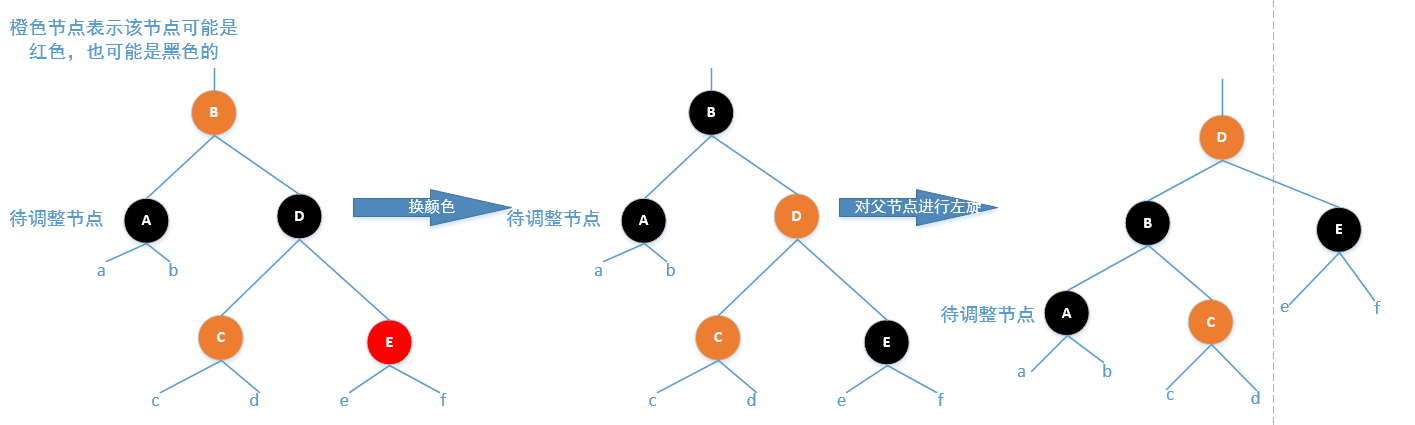
   从上图可以看出此时待调整节点所在的子树已经满足红黑树的性质,但是节点D如果是根节点那么不满足性质2,
   所以正对这种情况可以将待调整节点置为根节点即可
2. 当待调整节点为其父节点的右孩子时
   Case1:待调整节点的兄弟节点为红色
   调整方法:交换兄弟节点和其父节点的颜色,并对父节点进行一次右旋,右旋后待调整节点的兄弟节点发生了更
   换,重新记录兄弟节点
   
    
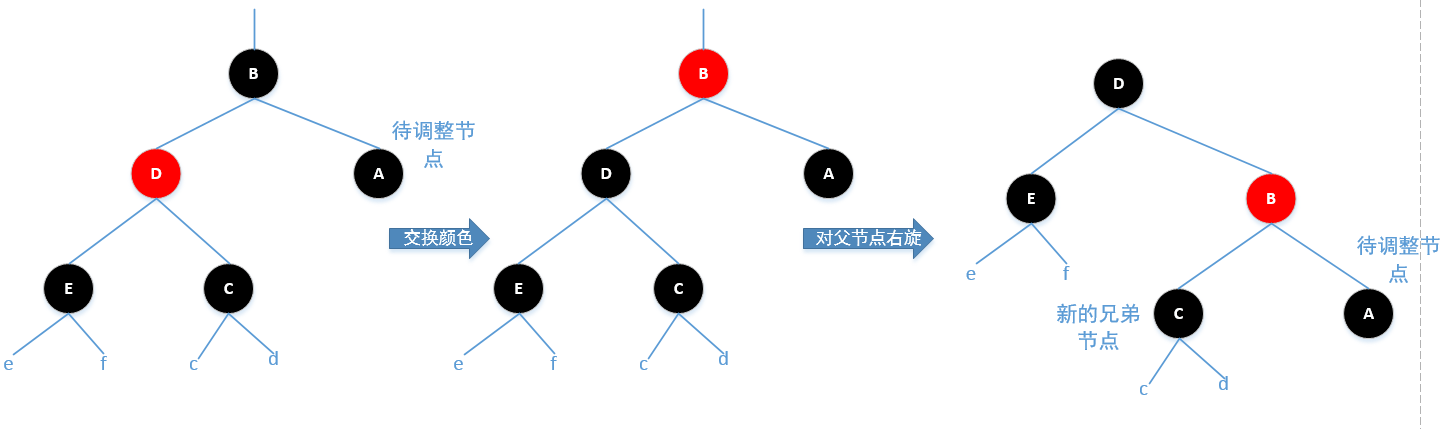
   Case2:待调整节点的兄弟节点是黑色的,父节点颜色任意,并且兄弟节点的左右孩子都为黑色
   调整方法:将兄弟节点置为红色,并将父节点置为下一次的待调整节点
   
    
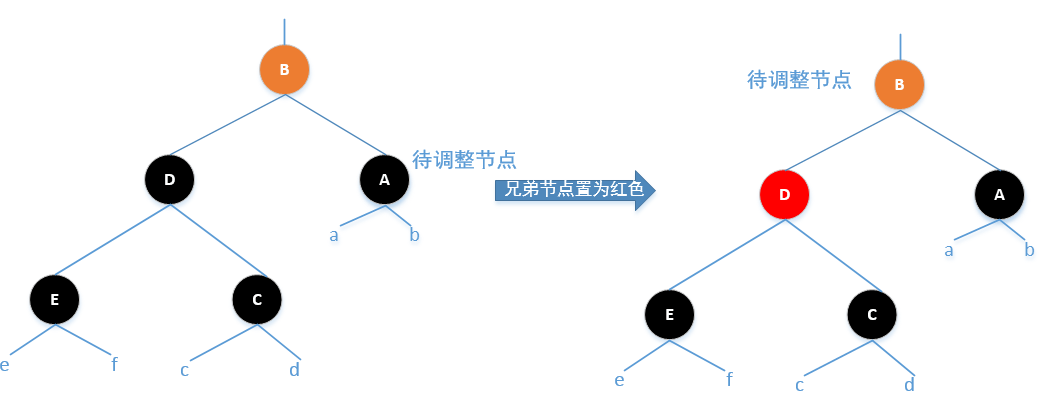
   Case3:待调整节点的兄弟节点为黑色,并且兄弟节点的左孩子为黑色,右孩子为红色
   调整方法:将兄弟节点的颜色和兄弟节点右孩子节点的颜色进行对换,然后对兄弟节点进行左旋
   
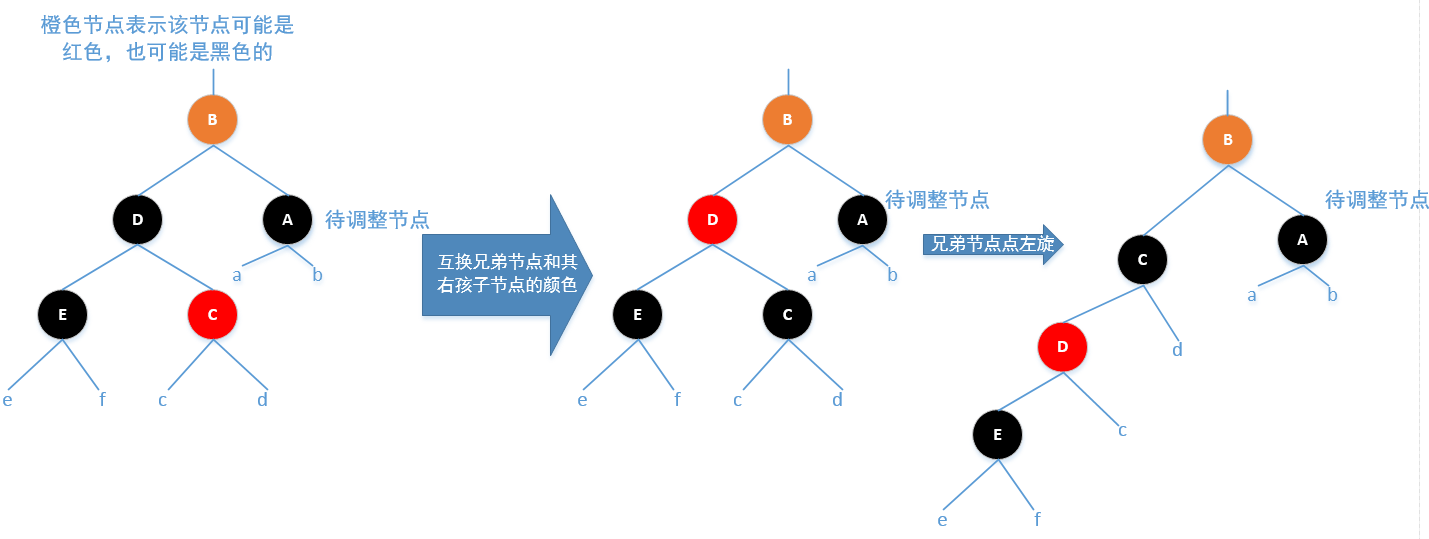
   Case4:待调整节点的兄弟节为黑色,并且兄弟节点的左孩子为红色,右孩子颜色任意
   调整方法:将兄弟节点的颜色置为父节点的颜色,然后将父节点置为黑色,将兄弟节点的左孩子置为黑色,然后对
   父节点进行右旋,最后将待调整节点置为根节点,如下图所示:
   

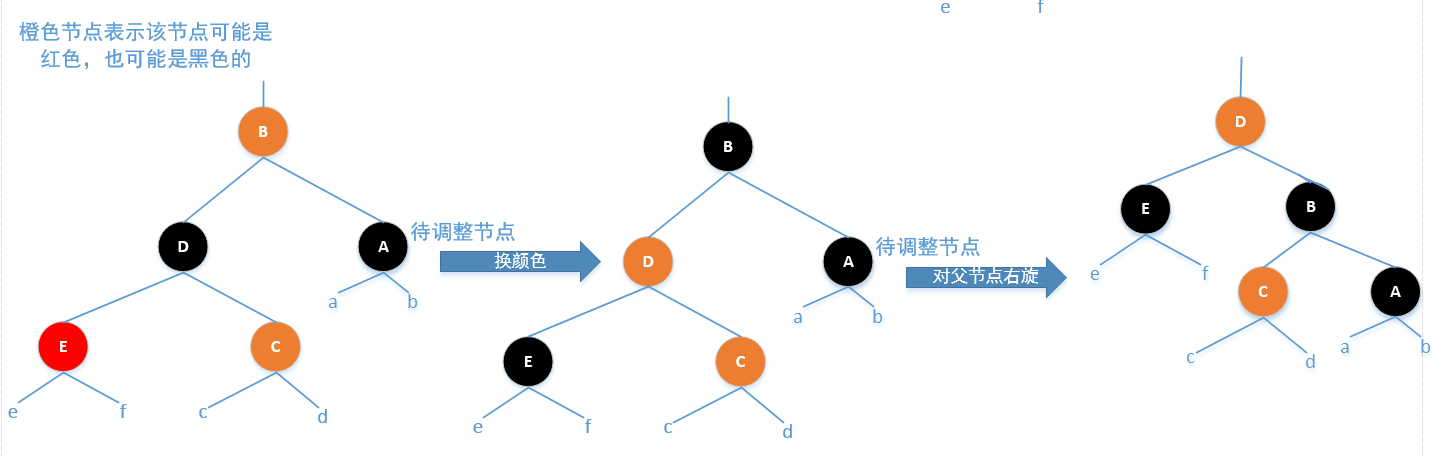
删除节点后调整代码的实现:

/************************************************************************
// 函数名称: CRBTree<T>::FixAfterDelete
// 访问权限: private
// 函数功能: 删除节点后,从pAdjustNode指向的节点开始进行调整
// 返回值:   bool
// 参数:     PRBNode<T> pAdjustNode:待调整节点位置
// 参数:     PRBNode<T> pParentOfAdjust:待调整节点的父节点
// 注意:
************************************************************************/
template<typename T>
bool CRBTree<T>::FixAfterDelete(PRBNode<T> pAdjustNode, PRBNode<T> pParentOfAdjust)
{
  PRBNode<T> pBrother = nullptr;
  PRBNode<T> pAdjust = pAdjustNode;
  PRBNode<T> pParent = pParentOfAdjust;
  while ((pAdjust == nullptr || IS_BLACK_COLOR(pAdjust)) && pAdjust != m_Root)
  {
    if (IS_LEFT_CHID(pParent,pAdjust))
    {
      pBrother = pParent->m_pRight;
      if(IS_RED_COLOR(pBrother))
      {
        /*Case1:待调整节点的兄弟节点为红色,将兄弟节点置为黑色,将父节点置为红色,并对父节点进行一次左旋*/
        SET_BLACK_COLOR(pBrother);
        SET_RED_COLOR(pParent);
        LRotate(pParent);
        pBrother = pParent->m_pRight;
      }

      if ((pBrother->m_pLeft == nullptr || IS_BLACK_COLOR(pBrother->m_pLeft)) &&
          (pBrother->m_pRight == nullptr || IS_BLACK_COLOR(pBrother->m_pRight)))
      {
        /*Case2:待调整节点的兄弟节点为黑色,且兄弟节点的左右孩子都是黑色的(不存在也视为黑色),则将兄弟节点
                置为红色,并将其父节点置为下一次的调整节点*/
        SET_RED_COLOR(pBrother);
        pAdjust = pParent;
        pParent = pAdjust->m_pParent;
      }
      else
      {
        /*此时兄弟节点的左孩子必定存在并且是红色的*/
        if (pBrother->m_pRight == nullptr || IS_BLACK_COLOR(pBrother->m_pRight))
        {
          /*Case3:兄弟节点是黑色的,兄弟节点的左孩子是红色,兄弟节点的右孩子是黑色(不存在也视为黑色),
                  将兄弟节点置为红色,兄弟节点的左孩子置为黑色,并对兄弟节点进行一次右旋*/
          SET_RED_COLOR(pBrother);
          SET_BLACK_COLOR(pBrother->m_pLeft);
          RRotate(pBrother);
          pBrother = pParent->m_pRight;
        }
        
        /*Case4:此时兄弟节点的右孩子必定是红色的,左孩子可有可无或者颜色任意,将父节点的颜色赋值给兄弟节点
                并将父节点置为黑色,在将兄弟节点的右孩子节点置为黑色,然后对父节点进行一次左旋,并将待调整
                节点置为根节点,则调整结束*/
        SET_COLOR(pBrother, GET_COLOR(pParent));
        SET_BLACK_COLOR(pParent);
        SET_BLACK_COLOR(pBrother->m_pRight);
        LRotate(pParent);
        pAdjust = m_Root;
      }
    }
    else
    {
      pBrother = pParent->m_pLeft;
      if (IS_RED_COLOR(pBrother))
      {
        /*Case1:待调整节点的兄弟节点为红色,将兄弟节点置为黑色,将父节点置为红色,并对父节点进行一次左旋*/
        SET_BLACK_COLOR(pBrother);
        SET_RED_COLOR(pParent);
        LRotate(pParent);
        pBrother = pParent->m_pRight;
      }

      if ((pBrother->m_pLeft == nullptr || IS_BLACK_COLOR(pBrother->m_pLeft)) &&
          (pBrother->m_pRight == nullptr || IS_BLACK_COLOR(pBrother->m_pRight)))
      {
        /*Case2:待调整节点的兄弟节点为黑色,兄弟节点的两个子节点也是黑色的,则将兄弟节点置为红色,
                并将父节点置为下一次的调整节点*/
        SET_RED_COLOR(pBrother);
        pAdjust = pParent;
        pParent = pAdjust->m_pParent;
      }
      else
      {
        if (pBrother->m_pLeft == nullptr || IS_BLACK_COLOR(pBrother->m_pLeft))
        {
          /*Case3:待调整节点的兄弟节点为黑色,兄弟的左孩子节点为黑色,右孩子节点为红色,则将兄弟节点置为红色,
                  将兄弟节点的右孩子置为黑色,并对兄弟进行左旋*/
          SET_RED_COLOR(pBrother);
          SET_BLACK_COLOR(pBrother->m_pRight);
          LRotate(pBrother);
          pBrother = pParent->m_pLeft;
        }

        /*Case3:此时待调整节点的兄弟节点是黑色的,兄弟节点的左孩子是红色的,将父节点的颜色赋值给兄弟节点,
                并将父节点置为黑色,将兄弟节点的左孩子置为黑色,并对父节点进行一次右旋,并将下次调整节点置
                为根节点,则调整结束*/
        SET_COLOR(pBrother, GET_COLOR(pParent));
        SET_BLACK_COLOR(pBrother->m_pLeft);
        SET_BLACK_COLOR(pParent);
        RRotate(pParent);
        pAdjust = m_Root;
      }
    }
  }

  SET_BLACK_COLOR(pAdjust);
  return true;
}

删除节点的时间复杂度分析

n个节点的红黑树的高度为lg(n),删除节点前查找节点的时间复杂度为O(lgn),在查找待删除节点右子树中最小
节点值的操作时间复杂度不超过O(lgn),在删除节点后修复过程中,对于Case1,3,4至多旋转3次就结束调整了,
所以时间复杂度为O(1),Case2情形下是循环可以重复执行的唯一情况,从叶节点调整到根节点最多耗时O(lgn),
所以整个删除操作时间复杂度为lgn

完整代码:https://github.com/xhqxhq/RBTree.git