Trie
原理
不讲了吧……就是一个点对应一个字符,很基本的思路。如果不会看 这里
模板
(代码取自 “Remember the Word” ,LA3942 )
void insert( char *s )
{
int l=strlen(s),u=0;
for ( int i=0; i<l; i++ )
{
int c=s[i]-'a';
if ( !tr[u][c] ) val[top]=0,tr[u][c]=top++;
u=tr[u][c];
}
val[u]=1;
}
int query( char *s,int st )
{
int cnt=0,u=0;
for ( int i=st; i<len; i++ )
{
int c=s[i]-'a'; u=tr[u][c];
if ( !u ) return cnt;
if ( val[u] ) (cnt+=d[i+1])%=mod;
}
return cnt;
}
练习
Fuzzy Google Suggest( UVA1462 )
题意:给定一个字符串集合,有n次搜索,每次有一个整数x和一个字符串,表示可以对字符串进行x次修改,
包括增加、修改和删除一个字符,问修改后的字符串可能是字符集中多少个字符串的前缀。
思路:首先对给出的字符串集建 Trie。对于每一次搜索操作,在 Trie 上进行两次 dfs(算上清理是3次,因为数据范围三百万不可能 memset ,代码中将计算贡献和清除一起写了)
第一次 dfs 对于搜索串进行处理,如果匹配那么直接搜索,否则减少一次剩余修改次数并继续搜索。这个过程中,为了计算贡献需要打 tag,如果是路径上经过的 Trie 节点就标记为1,如果是结尾就标记为2.
第二次 dfs 对tag数组清除,并累加第一次出现2的位置的贡献。
#include <bits/stdc++.h>
using namespace std;
const int N=3e6+10;
int n;
char str[21];
struct Trie
{
int siz,g[N][26],val[N],vis[N];
int dep,ans;
char s[21];
void init()
{
siz=1; val[0]=0; memset( g[0],0,sizeof(g[0]) );
}
void dfs( int p,int len,int x )
{
if ( x<0 ) return;
if ( vis[p]==0 ) vis[p]=1;
if( len==dep ) { vis[p]=2; return; }
int ch=s[len]-'a';
if ( g[p][ch] ) dfs( g[p][ch],len+1,x );
dfs( p,len+1,x-1 );
for ( int i=0; i<26; i++ )
if ( g[p][i] ) dfs( g[p][i],len,x-1 ),dfs( g[p][i],len+1,x-1 );
}
void clear( int p,int flag )
{
if ( vis[p]==0 ) return;
if ( flag && vis[p]==2 ) ans+=val[p],flag=0;
for ( int i=0; i<26; i++ )
if ( g[p][i] ) clear( g[p][i],flag );
vis[p]=0;
}
int calc( char *str,int x )
{
ans=0; dep=strlen(str); strcpy( s,str );
dfs( 0,0,x ); clear( 0,1 );
return ans;
}
void insert( char *str )
{
int p=0,n=strlen(str);
for ( int i=0; i<n; i++ )
{
int ch=str[i]-'a';
if ( g[p][ch]==0 )
{
val[siz]=0; memset( g[siz],0,sizeof(siz) );
g[p][ch]=siz++;
}
p=g[p][ch]; val[p]++;
}
}
}tr;
int main()
{
while ( scanf( "%d",&n )==1 )
{
tr.init();
for ( int i=0; i<n; i++ )
scanf( "%s",str ),tr.insert(str);
scanf( "%d",&n );
while ( n-- )
{
int x; scanf( "%s%d",str,&x );
printf( "%d
",tr.calc(str,x) );
}
}
}
KMP
原理
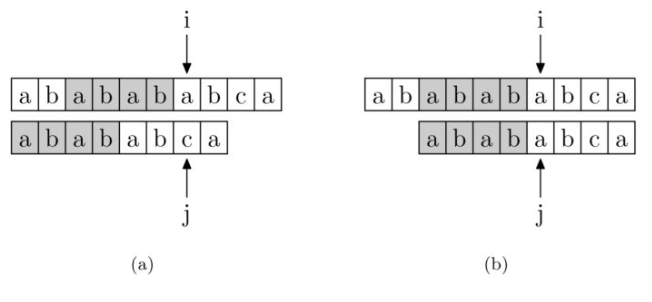
思想就是失配边,对于一个模板串 abbaaba ,如果匹配到最后一个字符失配,那么应该从模板串的第三个开始重新匹配。可以发现其实就是前后缀的匹配。关键在于状态转移图的构造,思想是自己匹配自己,递推得到。
模板
//P3375 【模板】KMP字符串匹配
//输出s2在s1中所有出现位置,和 s2长度为i的前缀的最长border
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int kmp[N],la,lb;
char a[N],b[N];
int main()
{
scanf( "%s",a+1 ); scanf( "%s",b+1 );
la=strlen( a+1 ); lb=strlen( b+1 );
int j;
for ( int i=2; i<=lb; i++ )
{
while ( j && b[i]!=b[j+1] ) j=kmp[j];
if ( b[j+1]==b[i] ) j++;
kmp[i]=j;
}
j=0;
for ( int i=1; i<=la; i++ )
{
while ( j>0 && b[j+1]!=a[i] ) j=kmp[j];
if ( b[j+1]==a[i] ) j++;
if ( j==lb ) printf( "%d
",i-lb+1 ),j=kmp[j];
}
for ( int i=1; i<=lb; i++ )
printf( "%d ",kmp[i] );
}
扩展KMP
解决问题
定义母串S,和字串T,设S的长度为n,T的长度为m,求T与S的每一个后缀的最长公共前缀,
设 (extend) 数组,(extend[i]) 表示 (T) 与 (S[i,n-1]) 的最长公共前缀,要求出所有 (extend[i](0<=i<n))。
思想
首先我们从左到右依次计算extend数组,在某一时刻,设extend[0...k]已经计算完毕,并且之前匹配过程中所达到的最远位置为P,所谓最远位置,严格来说就是 (i+extend[i]-1) 的最大值((0<=i<=k)),并且设取这个最大值的位置为 po,如在上一个例子中,计算extend[1]时,P=3,po=0。
现在要计算 (extend[k+1]) ,根据extend数组的定义,可以推断出 (S[po,P]=T[0,P-po]) ,从而得到 (S[k+1,P]=T[k-po+1,P-po]) ,令 (len=next[k-po+1]) ,分情况讨论:
第一种情况:(k+len<P)
如下图所示:
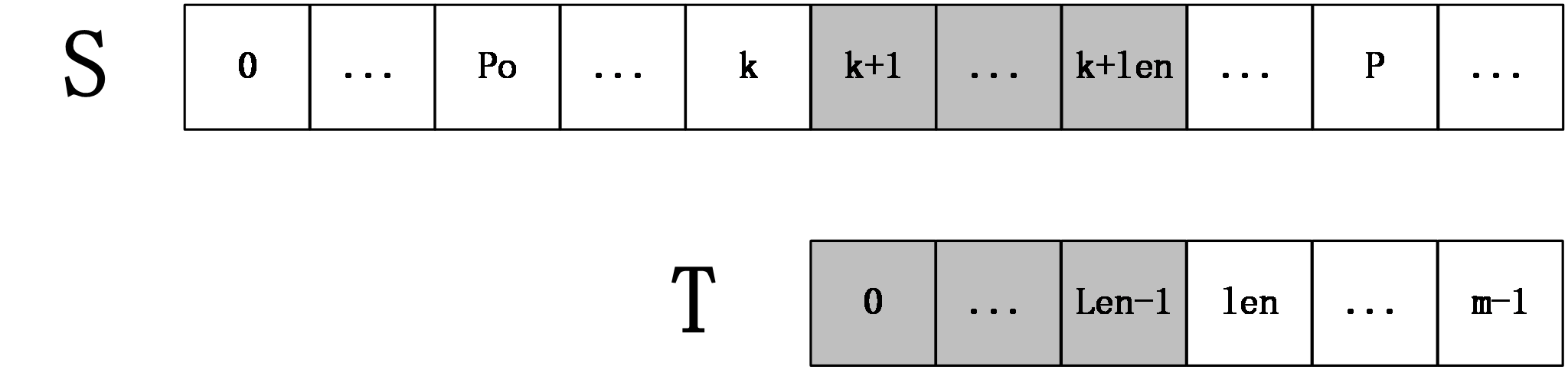
上图中,(S[k+1,k+len]=T[0,len-1]) ,然后 (S[k+len+1]) 一定不等于 (T[len]) ,因为如果它们相等,则有 (S[k+1,k+len+1]=T[k+po+1,k+po+len+1]=T[0,len]) ,那么 (next[k+po+1]=len+1) ,这和next数组的定义不符(next[i]表示T[i,m-1]和T的最长公共前缀长度),所以在这种情况下,不用进行任何匹配,就知道 (extend[k+1]=len)
第二种情况:$ k+len>=P$
如下图:
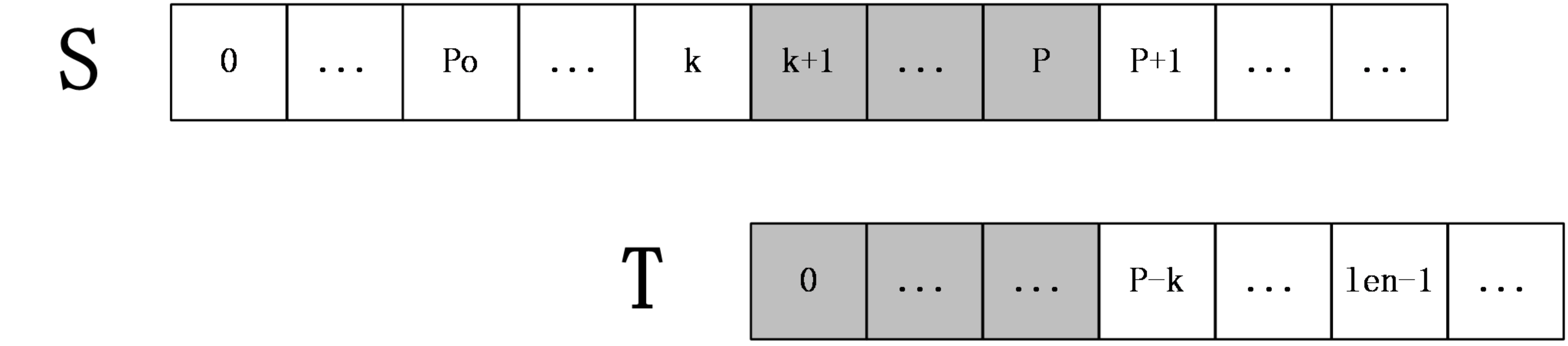
上图中,(S[p+1]) 之后的字符都是未知的,也就是还未进行过匹配的字符串,所以在这种情况下,就要从S[P+1]和 T[P-k+1] 开始一一匹配,直到发生失配为止,当匹配完成后,如果得到的 (extend[k+1]+(k+1)>P) 则要更新未知P和po。
计算 next 数组的过程和计算 extend[i] 的过程完全一样,将它看成是以T为母串,T为字串的特殊的拓展kmp算法匹配就可以了,计算过程中的next数组全是已经计算过的,所以按照上述介绍的算法计算next数组即可.
模板
const int maxn=100010; //字符串长度最大值
int next[maxn],ex[maxn]; //ex数组即为extend数组
//预处理计算next数组
void GETNEXT(char *str)
{
int i=0,j,po,len=strlen(str);
next[0]=len;//初始化next[0]
while(str[i]==str[i+1]&&i+1<len)//计算next[1]
i++;
next[1]=i;
po=1;//初始化po的位置
for(i=2;i<len;i++)
{
if(next[i-po]+i<next[po]+po)//第一种情况,可以直接得到next[i]的值
next[i]=next[i-po];
else//第二种情况,要继续匹配才能得到next[i]的值
{
j=next[po]+po-i;
if(j<0)j=0;//如果i>po+next[po],则要从头开始匹配
while(i+j<len&&str[j]==str[j+i])//计算next[i]
j++;
next[i]=j;
po=i;//更新po的位置
}
}
}
//计算extend数组
void EXKMP(char *s1,char *s2)
{
int i=0,j,po,len=strlen(s1),l2=strlen(s2);
GETNEXT(s2);//计算子串的next数组
while(s1[i]==s2[i]&&i<l2&&i<len)//计算ex[0]
i++;
ex[0]=i;
po=0;//初始化po的位置
for(i=1;i<len;i++)
{
if(next[i-po]+i<ex[po]+po)//第一种情况,直接可以得到ex[i]的值
ex[i]=next[i-po];
else//第二种情况,要继续匹配才能得到ex[i]的值
{
j=ex[po]+po-i;
if(j<0)j=0;//如果i>ex[po]+po则要从头开始匹配
while(i+j<len&&j<l2&&s1[j+i]==s2[j])//计算ex[i]
j++;
ex[i]=j;
po=i;//更新po的位置
}
}
}
练习
Generator( UVA1358 )
题意:有 (n) 种字符,给定一个模式串 (S) ,一开始字符串为空,现在每次随机生成一个 (1sim n) 的字符添加到字符串末尾,直到出现 (S) 停止,问长度期望。
思路:首先对 (S) 预处理,求出失配数组 fail。(dp[i]) 表示末尾匹配了 (i) 个 (S) 串所需要的次数期望,每次枚举可能出现的字符 (1sim n) 。对于 (S) 字符串,(i+1)肯定是确定的字符,所以对于其他字符肯定是不匹配的。假设现在生成了 (k) 字符,并且 (k) 字符不等于 (S[i+1]) ,那么根据 (S) 的 fail,假设有匹配 (j) 个字符,那么也就是说从匹配 (j) 个到匹配 (i) 个我们还要重新生成 (dp[i] - dp[j]) 次(期望)。
(从匹配 (i-1) 到匹配 (i) 个需要生成次数的期望)(f(i)=1+sum_{i=1}^n(dp[i-1]-dp[lose(k)])/n+dfrac{n-1}{n}f(i))
(lose(k)为生成字符k的情况下匹配的字符数)
$ dp[i] = dp[i-1] + f(i)$
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=21;
int fail[N],n;
ll f[N];
char s[N];
void get_fail( char *s )
{
int p=0,len=strlen(s+1);
for ( int i=2; i<=len; i++ )
{
while ( p && s[p+1]!=s[i] ) p=fail[p];
if ( s[p+1]==s[i] ) p++;
fail[i]=p;
}
}
int main()
{
int T; scanf( "%d",&T );
for ( int cas=1; cas<=T; cas++ )
{
printf( "Case %d:
",cas );
scanf( "%d%s",&n,s+1 );
get_fail(s); f[0]=0; int len=strlen(s+1);
for ( int i=1; i<=len; i++ )
{
f[i]=f[i-1]+n;
for ( int j=0; j<n; j++ )
{
if ( s[i]=='A'+j ) continue;
int p=i-1;
while ( p && s[p+1]!=j+'A' ) p=fail[p];
if ( s[p+1]==j+'A' ) p++;
f[i]+=f[i-1]-f[p];
}
}
printf( "%lld
",f[len] );
if ( cas<T ) printf( "
" );
}
}
关于 kmp 算法中 next 数组的周期性质
约定: (nxt[?]) 不同于 (nxt[i]) ,定义为 (nxt[i]) 的候选项之一。
结论
对于某一字符串 (S[1 o i]) ,在众多的 (nxt[i]) 候选项中,如果存在一个 (nxt[i]) 使得 (imod (i-nxt[i])==0) ,那么 (S[1 o (i-nxt[i])]) 可以成为 (S[1 o i]) 的循环节,循环次数为 (dfrac{i}{i-nxt[i]}) 。
推论1
若 (i-nxt[i]) 可以整除 (i) ,那么 (s[1 o i]) 具有长度为 (i-nxt[i]) 的循环节,即 (s[1 o i-nxt[i]]) 。
推论2
若 (i-nxt[?]) 整除 (i) ,那么 (s[1 o i ]) 具有长度为 (i-nxt[?]) 的循环节,即 (s[1 o i-nxt[?]]) 。
推论3
任意一个循环节长度必定是最小循环节长度倍数。
推论4
如果 (i-nxt[i]) 不能整除 (i) ,(s[1 o i-nxt[?]]) 一定不能作为循环节。
扩展
- 如果 (i-nxt[i]) 不能整除 (i) ,一定不存在循环节,(i-nxt[?]) 一定都不可整除
- 如果 (s[1 o m]) 是 (s[1 o i]) 的循环节,(nxt[i]) 一定为 (i-m) .
- (m-i-nxt[i],j=nxt[?]=>nxt[j]=j-m)
AC自动机
解决问题
多个模板串匹配一个文本串。
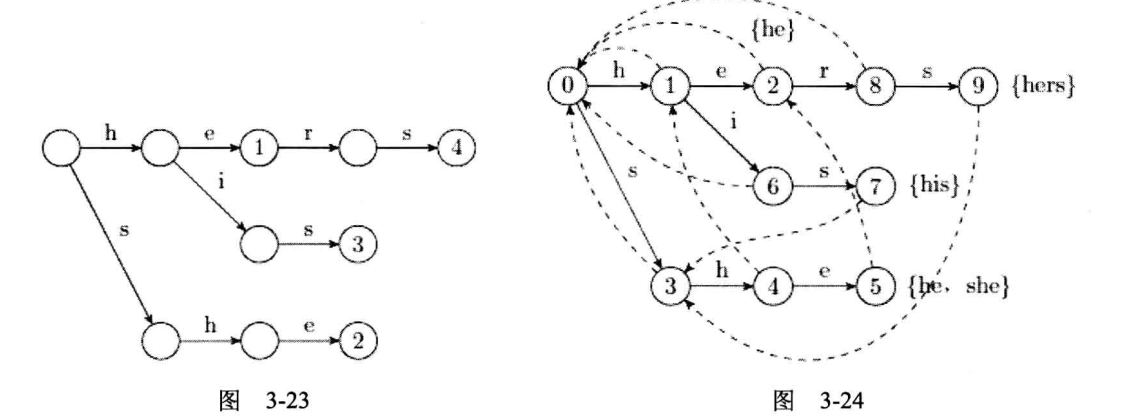
原理
大致思想是,KMP是线性的字符串加上失配边,AC自动机就是Trie加上失配边。 图解AC自动机
模板
//P3808 【模板】AC自动机(简单版)
//求有多少个不同的模式串在文本串里出现过。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e6+10;
int trie[N][26],cnt[N],fail[N],num=0,n;
string s;
void insert( string s )
{
int rt=0;
for ( int i=0; i<s.size(); i++ )
{
int nxt=s[i]-'a';
if ( !trie[rt][nxt] ) trie[rt][nxt]=++num;
rt=trie[rt][nxt];
}
cnt[rt]++;
}
void getfail()
{
queue<int> q;
for ( int i=0; i<26; i++ )
if ( trie[0][i] ) fail[trie[0][i]]=0,q.push(trie[0][i]);
while ( !q.empty() )
{
int now=q.front(); q.pop();
for ( int i=0; i<26; i++ )
if ( trie[now][i] )
{
fail[trie[now][i]]=trie[fail[now]][i];
q.push( trie[now][i] );
}
else trie[now][i]=trie[fail[now]][i];
}
}
int query( string s )
{
int now=0,res=0;
for ( int i=0; i<s.size(); i++ )
{
now=trie[now][s[i]-'a'];
for ( int j=now; j && cnt[j]!=-1; j=fail[j] )
res+=cnt[j],cnt[j]=-1;
}
return res;
}
int main()
{
scanf( "%d",&n );
for ( int i=0; i<n; i++ )
cin>>s,insert( s );
fail[0]=0; getfail();
cin>>s;
printf( "%d
",query(s) );
}
练习
/*
Puzzle(UVA1399)
题意:给定n,允许使用1~n的字符,给定一些禁止串,问不出现禁止串的最长字符串是否存在,
如果长度无限长或者不能构成都认为是不存在的。
思路:AC自动机+DP
看到事先给出的禁止串很容易想到AC自动机。在每个禁止串末尾节点打标记,fail树向上传递。
用 f[x] 表示 AC自动机上 从节点x开始往下,不经过尾标记的最大长度。有 f[x]=max( f[tr[x][ch]]+1 );
从根节点开始dfs,vis[x] 记录 x节点是否在当前路径上,如果 vis[x]=1,则说明出现了合法的循环,可以无限延伸。
记忆化: 记录x节点是否搜索过。
*/
#include <bits/stdc++.h>
using namespace std;
const int N=5e4+10;
int n,m,vis[N],f[N],sav[N][2],got[N];
char s[55];
struct ACmachine
{
int tr[N][26],val[N],nxt[N],sz;
void init()
{
sz=1; memset( tr[0],0,sizeof(tr[0]) );
}
void insert( char *str,int v=1 )
{
int len=strlen(str),p=0;
for ( int i=0; i<len; i++ )
{
int ch=str[i]-'A';
if ( !tr[p][ch] )
{
memset( tr[sz],0,sizeof(tr[sz]) );
val[sz]=0; tr[p][ch]=sz++;
}
p=tr[p][ch];
}
val[p]=v;
}
void getnxt()
{
queue<int> Q; nxt[0]=0;
for ( int ch=0; ch<n; ch++ )
{
int p=tr[0][ch];
if ( p ) { nxt[p]=0; Q.push(p); }
}
while ( !Q.empty() )
{
int now=Q.front(); Q.pop();
for ( int ch=0; ch<n; ch++ )
{
int p=tr[now][ch];
if ( !p ) { tr[now][ch]=tr[nxt[now]][ch]; continue; }
Q.push(p); int v=nxt[now];
while ( v && !tr[v][ch] ) v=nxt[v];
nxt[p]=tr[v][ch]; val[p]|=val[nxt[p]];
}
}
}
}AC;
bool find( int u )
{
got[u]=1;
for ( int i=0; i<n; i++ )
{
int v=AC.tr[u][i];
if ( vis[v] ) return 1;
if ( !got[v] && !AC.val[v] )
{
vis[v]=1;
if ( find(v) ) return 1;
vis[v]=0;
}
}
return 0;
}
int dfs( int u )
{
if ( vis[u] ) return f[u];
vis[u]=1; f[u]=0;
for ( int i=n-1; i>=0; i-- )
if ( !AC.val[AC.tr[u][i]] )
{
int tmp=dfs( AC.tr[u][i] )+1;
if ( f[u]<tmp )
{
f[u]=tmp; sav[u][0]=AC.tr[u][i]; sav[u][1]=i;
}
}
return f[u];
}
void write( int u )
{
if ( sav[u][0]==-1 ) return;
printf( "%c",sav[u][1]+'A' ); write( sav[u][0] );
}
int main()
{
int T; scanf( "%d",&T );
while ( T-- )
{
AC.init(); scanf( "%d%d",&n,&m );
while ( m-- )
scanf( "%s",s ),AC.insert(s);
AC.getnxt();
memset( got,0,sizeof(got) ); memset( vis,0,sizeof(vis) );
vis[0]=1;
if ( find(0) ) printf( "No
" );
else
{
memset( vis,0,sizeof(vis) ); memset( sav,-1,sizeof(sav) );
if ( dfs(0)==0 ) printf( "No
" );
else write(0),printf( "
" );
}
}
}
/*
GRE Words(UVA1502)
题意:给定一个单词表,每个单词有权值,取出一部分(不改变顺序)使得这部分的每一个字符串都是后一个的子串,问得到的最大权值。
思路:AC自动机+线段树优化DP。
设 f[i] 表示选了第 i 个字符串之后得到的最大值(截止)f[i]=max(f[j])+w[i], iff s[j]是s[i]的子串且j<i;
反向建 fail 树,那么对于串 s[i] 的最后一位指向的孩子,均是包含s[i]的串,所以 s[i] 最后一位的子树中孩子节点均包含 s[i]
那么对串 s[1]~s[n] 进行计算时,可以把结果用线段树更新到子树,计算时只需考虑s[i]的每一位能得到的最大值(单点查询),
最后取 max+w[i] 为 s[i] 最大值,更新即可。
*/
#include <bits/stdc++.h>
using namespace std;
const int N=2e4+10,M=3e5+10;
struct edge
{
int nxt,to;
}e[M];
char s[M];
int w[N],pos[N],tr[M][26],fail[M],rt,tot,head[M],cnt,n;
int in[M],out[M],tp,tx[M<<2],tf[M<<4],L,R,tmp;
int newnode()
{
tot++; memset( tr[tot],0,sizeof(tr[tot]) );
fail[tot]=0; return tot;
}
void add( int u,int v )
{
e[cnt].to=v; e[cnt].nxt=head[u]; head[u]=cnt++;
}
void insert( char *s )
{
int p=rt;
for ( int i=0; s[i]; i++ )
{
int ch=s[i]-'a';
if ( !tr[p][ch] ) tr[p][ch]=newnode();
p=tr[p][ch];
}
}
void build()
{
queue<int> q; q.push(rt);
while ( !q.empty() )
{
int now=q.front(); q.pop();
if ( now!=rt ) add( fail[now],now );
for ( int i=0; i<26; i++ )
if ( tr[now][i] )
{
if ( now!=rt ) fail[tr[now][i]]=tr[fail[now]][i];
q.push( tr[now][i] );
}
else tr[now][i]=tr[fail[now]][i];
}
}
void dfs( int now )
{
in[now]=++tp;
for ( int i=head[now]; i; i=e[i].nxt )
dfs( e[i].to );
out[now]=tp;
}
void pushdown( int i )
{
if ( !tf[i] ) return;
int pre=tf[i];
tf[i<<1]=max( tf[i<<1],pre ); tf[i<<1|1]=max( tf[i<<1|1],pre );
tx[i<<1]=max( tx[i<<1],pre ); tx[i<<1|1]=max( tx[i<<1|1],pre );
tf[i]=0;
}
int query( int l,int r,int p )
{
if ( l==r ) return tx[p];
int mid=(l+r)>>1;
pushdown(p);
if ( L<=mid ) return query( l,mid,p<<1 );
else return query( mid+1,r,p<<1|1 );
}
void update( int l,int r,int p )
{
if ( L<=l && r<=R )
{
tf[p]=max( tf[p],tmp ); tx[p]=max( tx[p],tmp ); return;
}
int mid=(l+r)>>1; pushdown(p);
if ( L<=mid ) update( l,mid,p<<1 );
if ( R>mid ) update( mid+1,r,p<<1|1 );
tx[p]=max( tx[p<<1],tx[p<<1|1] );
}
void init()
{
tot=-1; cnt=1; tp=0; rt=newnode();
memset( head,0,sizeof(head) ); memset( fail,0,sizeof(fail) );
memset( tx,0,sizeof(tx) ); memset( tf,0,sizeof(tf) );
}
int main()
{
int T; scanf( "%d",&T );
for ( int cas=1; cas<=T; cas++ )
{
init(); scanf( "%d",&n );
for ( int i=1; i<=n; i++ )
{
scanf( "%s%d",s+pos[i-1],w+i );
pos[i]=pos[i-1]+strlen(s+pos[i-1]); insert( s+pos[i-1] );
}
build(); dfs( rt ); int ans=0;
for ( int i=1; i<=n; i++ )
{
tmp=0; int now=rt;
for ( int j=pos[i-1]; j<pos[i]; j++ )
{
now=tr[now][s[j]-'a']; L=R=in[now];
int res=query( 1,tp,1 ); tmp=max( tmp,res );
}
tmp+=w[i]; ans=max( ans,tmp );
L=in[now]; R=out[now]; update( 1,tp,1 );
}
printf( "Case #%d: %d
",cas,ans );
}
}
后缀数组
解决问题
AC自动机解决了多模板匹配问题,前提是事先知道模板。后缀数组预处理文本串而不是模板。
原理
假定文本串为 BANANA ,那么在末尾加一个字符 $ ,然后把所有后缀插入到 Trie 中,(一个结点的孩子按字典序排序),在叶节点处标记该后缀的首字符在原串里面的下标。自左向右把所有叶节点的编号排列出来得到后缀数组,是所有后缀按照字典序从小到大排序的结果。
由于快排的复杂度是 (O(n^2logn)) ,所以采用某倍增算法 (O(nlogn)) (据说还有 (O(n)) 的)
首先把所有单个字符排序,计算每个的名次,然后给所有后缀的前两个字符排序,然后是前四个(注意,这里排序对象还是二元组,每个后缀k的前4个字符是k的前两个和k+2的前两个组成,比较时先比较k的前两个和k'的前两个,然后是k+2的前两个和k'+2的前两个),所有名次两两不同就不用排序了。排序二元组的时候可以用基数排序。
加强版
辅助数组:(rank)(后缀 (i) 在 sa 中的下标),(height)( (sa[i-1]) 和 (sa[i]) 的最长公共前缀LCP长度)
对于两个后缀 (j) 和 (k) ,设 (rank[j]<rank[k]) ,那么后缀 (j,k) 的LCP就等于 (min{height[rank[j]+1],height[rank[j]+2],...,height[rank[k]]}) ,相当于 (RMQ(height,rank[j]+1,rank[k]+1))
模板
//P3809 【模板】后缀排序
//把字符串的所有非空后缀按字典序从小到大排序,然后按顺序输出后缀的第一个字符在原串中的位置
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int x[N],y[N],c[N],sa[N],rk[N],height[N],wei[30],n,m;
char s[N];
void SA()
{
for ( int i=1; i<=n; i++ )
++c[x[i]=s[i]];
for ( int i=2; i<=m; i++ )
c[i]+=c[i-1];
for ( int i=n; i>=1; i-- )
sa[c[x[i]]--]=i;
for ( int k=1; k<=n; k<<=1 )
{
int num=0;
for ( int i=n-k+1; i<=n; i++ )
y[++num]=i;
for ( int i=1; i<=n; i++ )
if ( sa[i]>k ) y[++num]=sa[i]-k;
for ( int i=1; i<=m; i++ )
c[i]=0;
for ( int i=1; i<=n; i++ )
++c[x[i]];
for ( int i=2; i<=m; i++ )
c[i]+=c[i-1];
for ( int i=n; i>=1; i-- )
sa[c[x[y[i]]]--]=y[i],y[i]=0;
swap(x,y);
x[sa[1]]=1; num=1;
for ( int i=2; i<=n; i++ )
x[sa[i]]=(y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k]) ? num : ++num;
if ( num==n ) break;
m=num;
}
for ( int i=1; i<=n; i++ )
printf( "%d ",sa[i] );
}
void get_height()
{
int k=0;
for ( int i=1; i<=n; i++ )
rk[sa[i]]=i;
for ( int i=1; i<=n; i++ )
{
if ( rk[i]==1 ) continue;
if ( k ) --k;
int j=sa[rk[i]-1];
while ( j+k<=n && i+k<=n && s[i+k]==s[j+k] ) ++k;
height[rk[i]]=k;
}
putchar(10);
for ( int i=1; i<=n; i++ )
printf( "%d ",height[i] );
}
int main()
{
gets( s+1 );
n=strlen( s+1 ); m=122;
SA();
}
Manacher
解决问题
最长回文子串:给定一个字符串,求它的最长回文子串长度。
原理
从中心扩展延伸的方法的缺陷:处理字符串长度的奇偶性带来的对称轴不确定问题
解决方案,对原来的字符串进行处理,在首尾和所有空隙插入一个无关字符,插入后不改变原串中回文的性质,但串长都变成了奇数.
定义:回文半径:一个回文串中最左或最右位置的字符到其对称轴的距离 ,用 (p[i]) 表示第 (i) 个字符的回文半径.
char : # a # b # c # b # a #
p[i] : 1 2 1 2 1 6 1 2 1 2 1
p[i] - 1 : 0 1 0 1 0 5 0 1 0 1 0
i : 1 2 3 4 5 6 7 8 9 10 11
显然,最大的 (p[i]−1) 就是答案
插入完字符之后对于一个回文串的长度为 原串长度*2+1,等于 这个回文串回文半径*2+1,显然相等。
这样问题就转换成了怎样快速的求出 (p) 。用 (mx) 表示所有字符产生的最大回文子串的最大右边界, (id) 表示产生这个边界的对称轴位置。
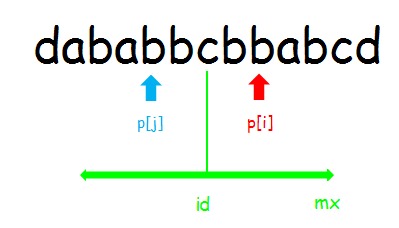
设已经求出了(p[1...7]) ,当 (i<mx) ,因为 (id) 被更新过了,而 (i) 是 (id) 之后的位置,第 (i) 个字符一定落在 (id) 右边。
记 串 (i) 表示以 (i) 为对称轴的回文串,(j) 和 (id) 同理。
情况1:i < mx
利用回文串的性质,对于 (i) ,可以找到一个关于 (id) 对称的位置 (j=id∗2−i) ,进行加速查找
(1)
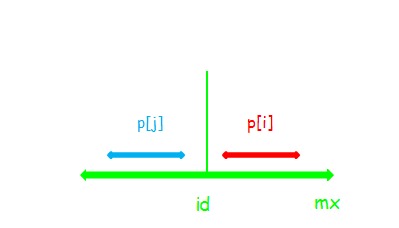
显然 (p[i]=p[j]) ,串 (i) 不可以再向两边扩张。如果可以的话,(p[j]) 也可以再扩张,而 (p[j]) 已经确定了。
(2)
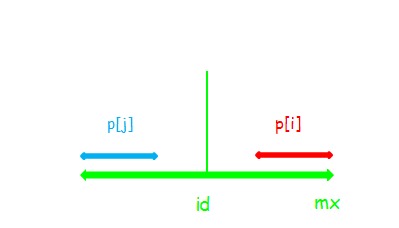
此时 (p[i]=p[j]) ,与(1)不同的是,串 (i) 是可以再扩张的。
(3)
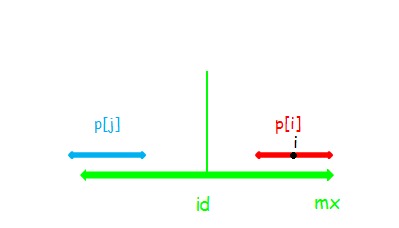
此时 (p[i]=mx−i) ,这时只能确定 串 (i) 在 (mx) 以内的部分是回文的,并不能确定串 (i) 和 串 (j) 相同。
同样,这时串 (i) 是不可以再向两端扩张的。
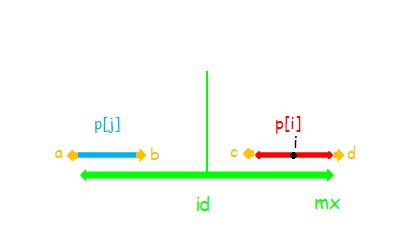
如果可以扩张,如图(这里的假设是 (p[j]>p[i]) ,那么 (p[j]ge p[i]+1) ,截取 (a,b) 使得和扩张 (1) 之后的 (i) 相同显然不会影响正确性),则 (d=c) ,根据对称性 (c=b) ,又因为 (a=b) ,所以 (a=d) ,串 (id) 可以继续扩张,但 (p[id]) 已经固定了.
情况2:i >= mx
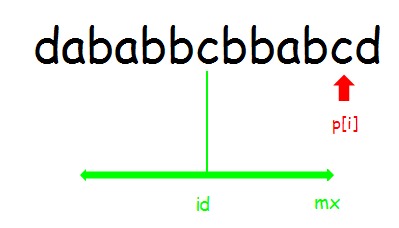
(p[i]=1)
模板
//P3805 【模板】manacher算法
//求最长回文串的长度
#include <bits/stdc++.h>
using namespace std;
const int N=22000010;
char s[N],str[N];
int pos[N];
int init() //处理原字符串
{
int len=strlen(s);
str[0]='@'; str[1]='#'; //@是防止越界
int j=2;
for ( int i=0; i<len; i++ )
str[j++]=s[i],str[j++]='#';
str[j]='�'; return j;
}
int manacher()
{
int ans=-1,len=init(),mx=0,id=0;
for ( int i=1; i<len; i++ )
{
if ( i<mx ) pos[i]=min( pos[id*2-i],mx-i ); //situation1
else pos[i]=1; //situation2
while ( str[i+pos[i]]==str[i-pos[i]] ) pos[i]++; //扩展
if ( pos[i]+i>mx ) mx=pos[i]+i,id=i; //update id
ans=max( ans,pos[i]-1 );
}
return ans;
}
int main()
{
scanf( "%s",s );
printf( "%d",manacher() );
}
练习
Casting Spells(UVA1470)
题意:问给定字符串中最大的W串的长度。其中W串的定义:形式为 ww'ww' 的字符串,w' 为 w 的反串
思路:虽然训练指南上没有讲 Manacher……但是这题几乎就是一个裸的 Manacher啊……
根据题目描述,显然 ww'ww' 和 ww' 都是回文串。
考虑 Manacher 的原理,不重不漏地枚举了每个回文串,也就是说考虑到了每一个回文串。
先回归暴力,想到可以枚举每个回文串并判断右边是否也是相同的一个回文串。
“枚举每个回文串”,和 Manacher 有相似之处。也就是说,我们是否可以在 Manacher 的运行过程中就完成答案统计?
设现在处理到了第 i 个位置,根据 Manacher 把奇数串转化成偶数串的思想,要求 i 是分隔符 #.
当 i 位置的回文半径达到 4 的倍数的时候,说明左半边的串长度是偶数,设当前回文半径为 r,显然左半边串的中心位置 (pos=i-r/2
),如果 pos 处的回文半径不小于 (i-r/2) ,那么左半边就是回文串,(ans=max( ans,r )).
#include <bits/stdc++.h>
using namespace std;
const int N=3e5+10;
int n,r[N<<1];
char str[N],s[N<<1];
void manacher()
{
int mx=0,pos=0,len=2*n+1,ans=0;
for ( int i=0; i<len; i++ )
{
if ( i<mx ) r[i]=min( r[2*pos-i],mx-i );
else r[i]=1;
while ( i+r[i]<len && i-r[i]>=0 && s[i+r[i]]==s[i-r[i]] )
{
if ( s[i]=='#' && r[i]%4==0 && r[i-r[i]/2]>=r[i]/2 ) ans=max( ans,r[i] );
r[i]++;
}
if ( i+r[i]>mx ) mx=i+r[i],pos=i;
}
printf( "%d
",ans );
}
void prework()
{
int pos=0; n=strlen(str);
for ( int i=0; i<n; i++ )
s[pos++]='#',s[pos++]=str[i];
s[pos++]='#';
}
int main()
{
int T; scanf( "%d",&T );
while ( T-- )
{
scanf( "%s",str ); prework();
manacher();
}
}
最小表示法
定义
字典序最小的循环同构串。(就是整体左移或右移,环状)
原理
考虑两个字符串 $A,B $ ,在 (S) 中的起始位置为 (i,j) ,且前 (k) 位相等。 如果 (A[i+k]>B[j+k]) ,那么对于任何一个字符串 (T) ,开头位于 (i o i+k) 之间,一定不会成为最优解。所以 (i) 可以直接跳到 (i+k+1)
复杂度 (O(n)).
模板
//UVA719 Glass Beads
//【模板】最小表示法
// 环形字符串,找个位置切开,使得字典序最小,输出最小切开的位置
#include <bits/stdc++.h>
using namespace std;
const int N=3e4+10;
int n,len;
char s[N];
int read()
{
int x=0,w=1; char ch=getchar();
while ( ch>'9' || ch<'0' ) { if ( ch=='-' ) w=-1; ch=getchar(); }
while ( ch<='9' && ch>='0' ) x=x*10+ch-'0',ch=getchar();
return x*w;
}
void solve()
{
scanf( "%s",s ); len=strlen( s );
int k=0,i=0,j=1;
while ( k<len && i<len && j<len )
{
int tmp=s[(i+k)%len]-s[(j+k)%len];
if ( tmp==0 ) k++;
else
{
if ( tmp<0 ) j+=k+1;
if ( tmp>0 ) i+=k+1;
if ( i==j ) ++i;
k=0;
}
}
printf( "%d
",min(i,j)+1 );
}
int main()
{
n=read();
for ( int cas=1; cas<=n; cas++ )
solve();
}