2021-09-23至2021-10-30关于transformer的学习

Transformer的提出解决了两个问题:
(1) 首先它使用了Attention机制,将序列中的任意两个位置之间的距离是缩小为一个常量;
(2) 其次它不是类似RNN(不能并行)的顺序结构,因此具有更好的并行性,符合现有的GPU框架。
transformer由多个编码器和解码器构成,其中编码器包括:self-attention(自注意力)和feed forward netword(前馈网络);解码器包括:自注意力,编码解码注意力和前馈网络。下面具体介绍各个部分。
一、encoder:
Embedding(嵌入):
与one-hot编码相比embedding将大型稀疏向量转换为保留语义关系的低维空间。
原始句子的单词长度是length=4,即‘我’ ‘爱’ ‘机器’ ‘学习’。经过embedding后每个词的embedding向量是512。那么“我爱机器学习”这个句子的embedding后的维度是[4,512 ] (若是批量输入,则embedding后的维度是[batch, 4, 512])。
Padding(填充):
因为每个样本的原始句子的长度是不一样的,假设样本中句子的最大长度是10,那么对于长度不足10的句子,需要补足到10个长度,shape就变为[10, 512], 补全的位置上的embedding数值自然就是0了。
Padding Mask:对于输入序列一般我们都要进行padding补齐,也就是说设定一个统一长度N,在较短的序列后面填充0到长度为N。对于那些补零的数据来说,我们的attention机制不应该把注意力放在这些位置上,所以我们需要进行一些处理。具体的做法是,把这些位置的值加上一个非常大的负数(负无穷),这样经过softmax后,这些位置的权重就会接近0。Transformer的padding mask实际上是一个张量,每个值都是一个Boolean,值为false的地方就是要进行处理的地方。
Positional Embedding(位置编码)
得到补全后的句子embedding向量后,直接输入encoder的话,那么是没有考虑到句子中的位置顺序关系的。此时需要再加一个位置向量,位置向量在模型训练中有特定的方式,可以表示每个词的位置或者不同词之间的距离;总之,核心思想是在attention计算时提供有效的距离信息。
关于positional embedding ,文章提出两种方法:
1.Learned Positional Embedding ,这个是绝对位置编码,即直接对不同的位置随机初始化一个postion embedding,这个postion embedding作为参数进行训练。
2.Sinusoidal Position Embedding ,相对位置编码,即三角函数编码。
下面详细讲下Sinusoidal Position Embedding 三角函数编码。
Positional Embedding和句子embedding是add操作,那么自然其shape是相同的也是[10, 512] 。transformer的输入是Word Embedding + Position Embedding。
Sinusoidal Positional Embedding具体怎么得来呢,我们可以先思考下,使用绝对位置编码,不同位置对应的positional embedding固然不同,但是位置1和位置2的距离比位置3和位置10的距离更近,位置1和位置2与位置3和位置4都只相差1。
这些关于位置的相对含义,模型能够通过绝对位置编码参数学习到吗?此外使用Learned Positional Embedding编码,位置之间没有约束关系,需要网络训练大量参数,我们只能期待它隐式地学到,是否有更合理的方法能够显示的让模型理解位置的相对关系呢?
肯定是有的,首先由下述公式得到Embedding值:
对于句子中的每一个字,其位置pos∈[0,1,2,…,9](假设每句话10个字), 每个字是N(512)维向量,维度 i (i∈[ 0,1,2,3,4,..N])带入函数

?:由于正弦函数能够表达相对位置信息,那么对每个positional embedding进行 sin 或者cos激活,可能效果更好,那就再将偶数列上的embedding值用sin()函数激活,奇数列的embedding值用cos()函数激活得到的具体示意图如下:

这样使用三角函数设计的好处是位置 i 处的单词的psotional embedding可以被位置 i+k 处单词的psotional embedding线性表示,反应两处单词的其相对位置关系。此外位置i和i+k的psotional embedding内积会随着相对位置的递增而减小,从而表征位置的相对距离。
但是不难发现,由于距离的对称性,Sinusoidal Position Encoding虽然能够反映相对位置的距离关系,但是无法区分i和i+j的方向。即pe(i)*pe(i+j) =pe(i)*pe(i-k)
另外,从参数维度上,使用三角函数Position Encoding不会引入额外参数,Learned Positional Embedding增加的参数量会随序列语句长度线性增长。在可扩展性上,Learned Positional Embedding可扩展性较差,只能表征在max_seq_length以内的位置,而三角函数Position Encoding没有这样的限制,可扩展性更强。
attention(注意力层)

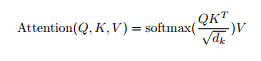

每个头Zi的结果是64维,最终的输出是512维
单头attention 的 Q/K/V 的shape和多头attention 的每个头的Qi/Ki/Vi的大小是不一样的,假如单头attention 的 Q/K/V的参数矩阵WQ/WK/WV的shape分别是[512, 512](此处假设encoder的输入和输出是一样的shape),那么多头attention (假设8个头)的每个头的Qi/Ki/Vi的参数矩阵WQi/WKi/WVi大小是[512, 512/8]。
add&Norm
使用残差residual connection
避免梯度消失。
残差连接对应的是每个block中的add
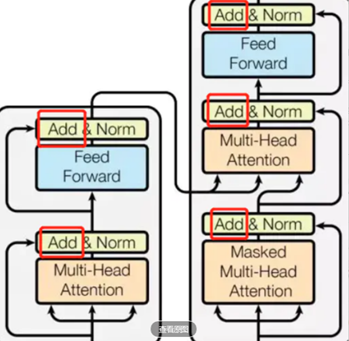
残差连接示意图如下。

残差连接
假设网络中某个层对输入x作用(比如使用Relu作用)后的输出是,那么增加residual connection之后,就变成了:这个+x操作就是一个shortcut。
那么残差结构有什么好处呢?显而易见:因为增加了一项x,那么该层网络对x求偏导的时候,多了一个常数项1。在反向传播过程中,梯度连乘,也不会造成梯度消失。
FeedForward(前馈网络)
全连接,隐藏层维度为2048,输入输出均为512
2.decoder
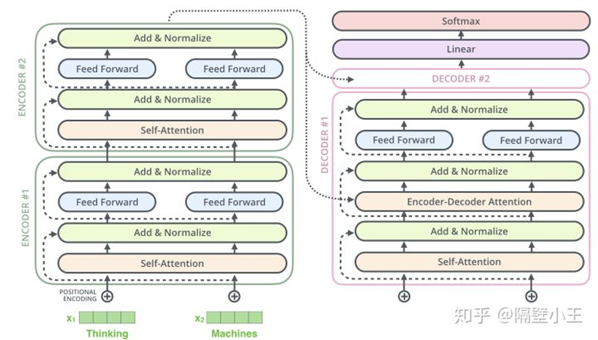
注意encoder的输出并没直接作为decoder的直接输入。
训练的时候,1.初始decoder的time step为1时(也就是第一次接收输入),其输入为一个特殊的token,可能是目标序列开始的token(如<BOS>),也可能是源序列结尾的token(如<EOS>),也可能是其它视任务而定的输入等等,不同源码中可能有微小的差异,其目标则是预测翻译后的第1个单词(token)是什么;2.然后<BOS>和预测出来的第1个单词一起,再次作为decoder的输入,得到第2个预测单词;3后续依此类推;
具体的例子如下:
样本:“我/爱/机器/学习”和 "i/ love /machine/ learning"
训练:
1. 把“我/爱/机器/学习”embedding后输入到encoder里去,最后一层的encoder最终输出的outputs [10, 512](假设我们采用的embedding长度为512,而且batch size = 1),此outputs 乘以新的参数矩阵,可以作为decoder里每一层用到的K和V;
2. 将<bos>作为decoder的初始输入,将decoder的最大概率输出词 A1和‘i’做cross entropy计算error。
3. 将<bos>,"i" 作为decoder的输入,将decoder的最大概率输出词 A2 和‘love’做cross entropy计算error。
4. 将<bos>,"i","love" 作为decoder的输入,将decoder的最大概率输出词A3和'machine' 做cross entropy计算error。
5. 将<bos>,"i","love ","machine" 作为decoder的输入,将decoder最大概率输出词A4和‘learning’做cross entropy计算error。
6. 将<bos>,"i","love ","machine","learning" 作为decoder的输入,将decoder最大概率输出词A5和终止符</s>做cross entropy计算error。
Sequence Mask
上述训练过程是挨个单词串行进行的,那么能不能并行进行呢,当然可以。可以看到上述单个句子训练时候,输入到 decoder的分别是
<bos>
<bos>,"i"
<bos>,"i","love"
<bos>,"i","love ","machine"
<bos>,"i","love ","machine","learning"
那么为何不将这些输入组成矩阵,进行输入呢?这些输入组成矩阵形式如下:
将decoder在上述2-6步次的输入补全为一个完整的句子
[<bos>,"i","love ","machine","learning"
<bos>,"i","love ","machine","learning"
<bos>,"i","love ","machine","learning"
<bos>,"i","love ","machine","learning"
<bos>,"i","love ","machine","learning"]
然后将上述矩阵矩阵乘以一个 mask矩阵
[1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 1 1 0
1 1 1 1 1 ]
这样是不是就得到了
[<bos>
<bos>,"i"
<bos>,"i","love"
<bos>,"i","love ","machine"
<bos>,"i","love ","machine","learning" ]
这样的矩阵了 。着就是我们需要输入矩阵。这个mask矩阵就是 sequence mask,其实它和encoder中的padding mask 异曲同工。
这样将这个矩阵输入到decoder(其实你可以想一下,此时这个矩阵是不是类似于批处理,矩阵的每行是一个样本,只是每行的样本长度不一样,每行输入后最终得到一个输出概率分布,作为矩阵输入的话一下可以得到5个输出概率分布)。这样我们就可以进行并行计算进行训练了。
test的时候 decoder不需要sequencen mask,因为test的时候是不知道未来要翻译出来的句子的全貌的,自然只能反复输入得到最终完整翻译的句子
测试
训练好模型, 测试的时候,比如用 '机器学习很有趣'当作测试样本,得到其英语翻译。这一句经过encoder后得到输出tensor,送入到decoder(并不是当作decoder的直接输入):
1.然后用起始符<bos>当作decoder的 输入,得到输出 machine
2. 用<bos> + machine 当作输入得到输出 learning
3.用 <bos> + machine + learning 当作输入得到is
4.用<bos> + machine + learning + is 当作输入得到interesting
5.用<bos> + machine + learning + is + interesting 当作输入得到 结束符号<eos>
我们就得到了完整的翻译 'machine learning is interesting'
可以看到,在测试过程中,只能一个单词一个单词的进行输出,是串行进行的。