A. K-th Largest Value

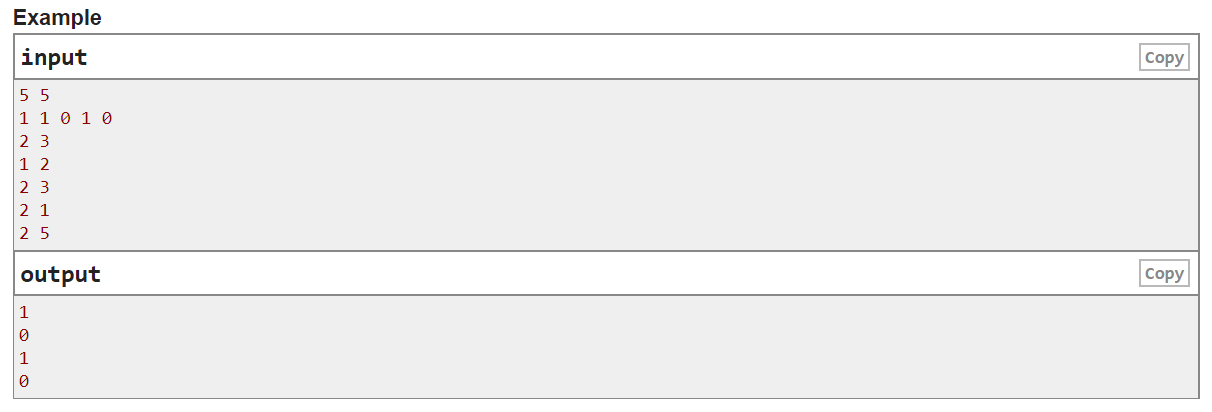
题意:数组a有n个0或者1,给q次操作,操作有两种,第一种ax->1-ax,第二种输出第k大元素
题解:标准水题,统计1的个数,进行第一种操作的时候更新1的个数即可,输出第k大元素时,看有无k个1,有就输出1,无就输出0
code:
#include<bits/stdc++.h> using namespace std; #define ll long long const int maxn = 1e5+10; int a[maxn]; int num; int main() { int n,q; scanf("%d%d",&n,&q); for(int i = 1; i <= n;i++) { scanf("%d",&a[i]); if(a[i]) num++; } for(int i = 0; i < q;i++) { int id; scanf("%d",&id); if(id == 1) { int x; scanf("%d",&x); a[x] = 1 - a[x]; if(a[x] == 1) num++; else num--; } else { int x; scanf("%d",&x); if(x <= num) printf("1 "); else printf("0 "); } } //system("pause"); return 0; }
B. Minimal Cost
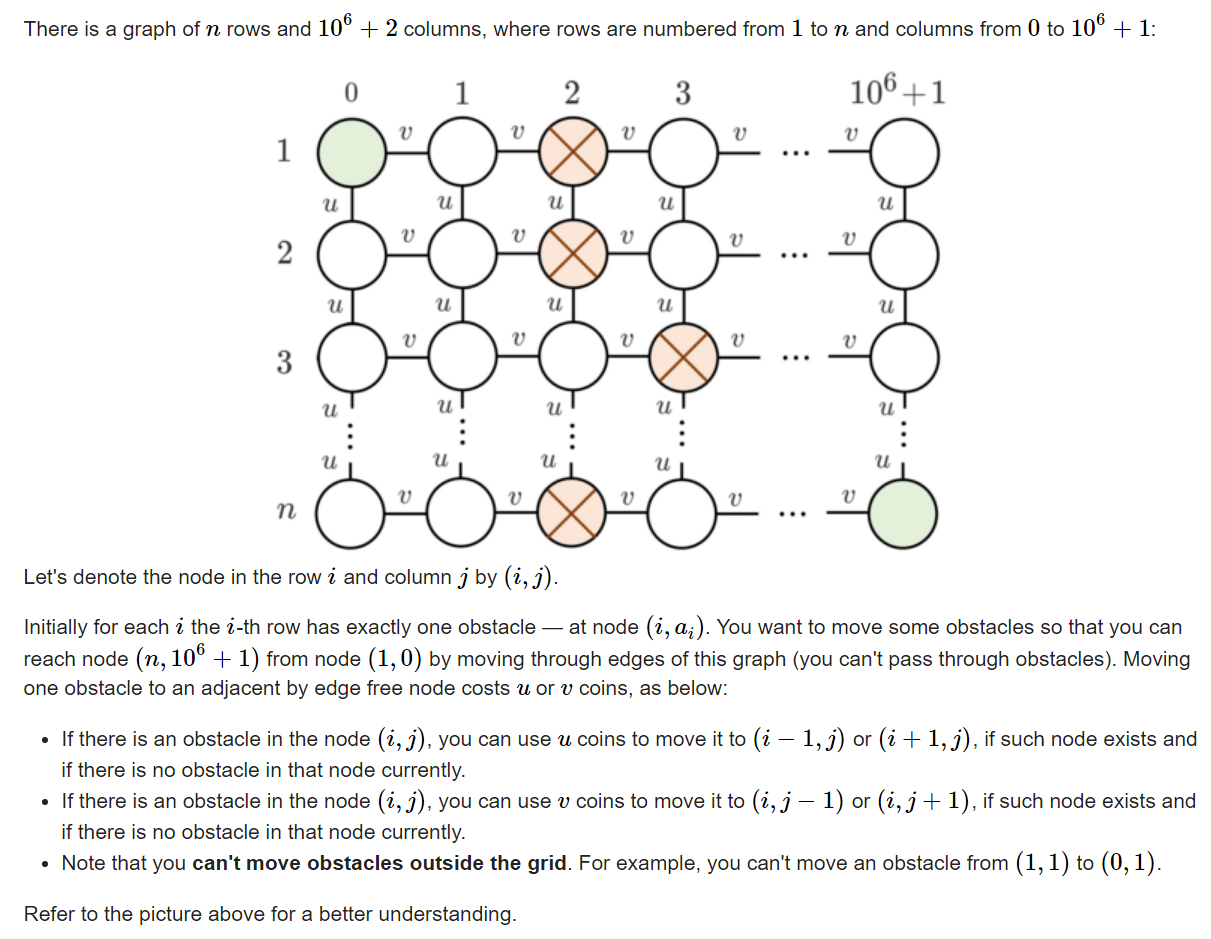
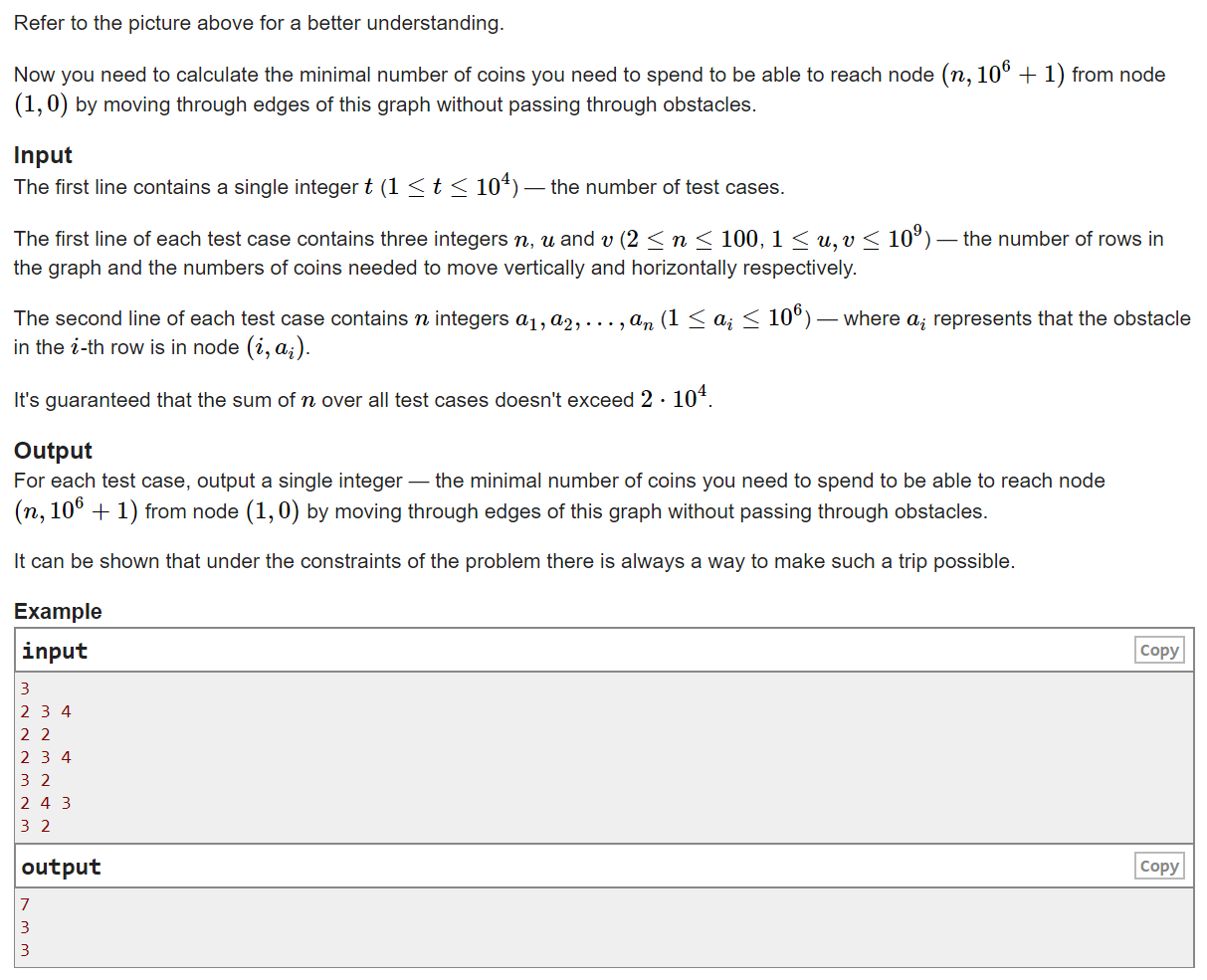
题意:给定n行,106+2列,每一行有一个障碍,障碍不出现在第0行和第106+1行,可以花费费用u垂直移动障碍,花费费用v水平移动障碍,问对该网络一个人可以从左上角走到右下角,最小花费
题解:分类讨论,如果所有障碍在同一列,那么要么平移两次,要么平移一次垂直动一次,答案为min(2*v,u+v);如果存在相邻行障碍所在列差值最大为1,那么要么平移一次,要么垂直移一次,答案为min(u,v);如果存在相邻行所在列差值大于等于2,答案为0
code:
#include<bits/stdc++.h> using namespace std; #define ll long long const int maxn = 1e6+10; int a[maxn]; int num; int main() { int t; scanf("%d",&t); for(int i=0; i<t; i++) { memset(a,0,sizeof(a)); int n; ll u,v; scanf("%d%lld%lld",&n,&u,&v); int ok = 1; int ansok = 1; int last = 0; for(int i = 0; i < n; i++) { scanf("%d",&a[i+1]); if(i != 0) { if(a[i+1] != last) ok = 0; if(abs(a[i+1] - a[i]) >=2 ) ansok = 0; } last = a[i+1]; } if(!ansok) printf("0 "); else if(ok) { printf("%lld ",min(2*v,u+v)); } else printf("%lld ",min(u,v)); } //system("pause"); return 0; }
C. Pekora and Trampoline

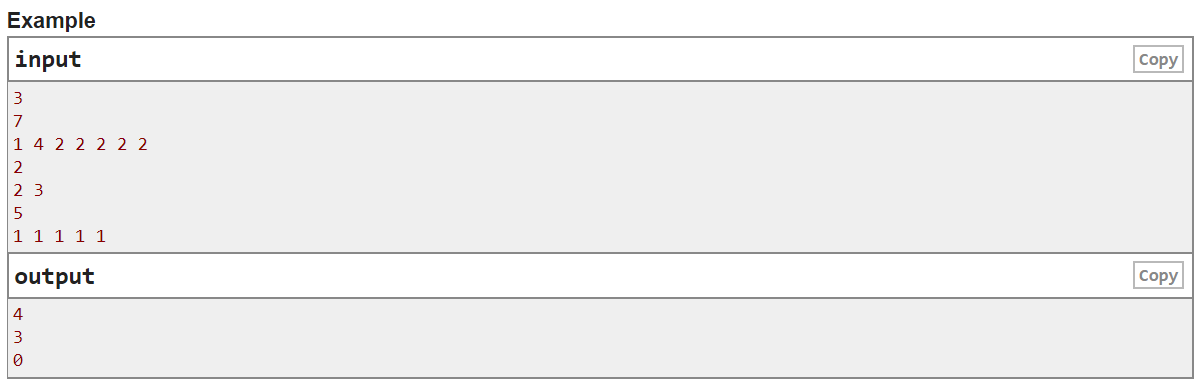
题意:给定一个长度为n的序列S,一个人可以从任何位置i起跳,下一步跳到i+Si,一直跳直到跳出n,每在一个位置i跳一次,对应位置Si减一,问多少次这个人会把序列S跳为全1
题解:贪心,每轮从前面的Si不为1的位置i起跳最优,并且该位置的Si一定会跳到1,那么对[i+2,min(i+Si,n)]这个区间的所有位置的Si都有-1的贡献,并且如果该位置的Si已经跳到1后,如果还跳到这个位置x次,那么一定对位置i+1有-x的贡献。
设立数组last[i],代表位置i已经被踩了多少次。从头遍历所有位置,寻找起跳点,对于当前的起跳点i,对答案ans的贡献为ans = S[i] - last[i] - 1(这样该点的Si会跳为1),last[i]更新为last[i] += S[i] - last[i] -1,对last[i+1]的贡献为last[i+1] += last[i] - S[i] + 1(跳到1后还跳了几次),对S[j]的贡献为S[j] - 1,j ∈ [i+2,min(i+Si,n)]。
code:
D. Zookeeper and The Infinite Zoo
题意:u可以达到u+v的充要条件为u&v = v,给定一系列a、b,问a能否到达b
题解:
①首先确定这不是图论!【好像没什么卵用的发现】
②通过观察发现u&v = v这个条件代表着u和从u自身二进制为1的那些位取出部分组成的数相&,一定满足u&v = v(例如u = 000111,v = 000100/000010/000001/000110等都满足条件) 【好像也是没什么卵用的发现】
③如果能够从u到达x;根据位运算的知识,u的任何一位1都可以通过相加进行左移,但不可以右移,也就是如果x的1的位置在u的1的位置的左边,就可以从u到达v
写法:从右往左比对x和u的每一位i,如果u[i] = 1,num++,如果x[i] = 1,num--,如果在某一位num < 0,那么不可达,否则可达(例如000010可以达到001000,是因为从右侧开始i = 2时, num + 1= 1,到了i = 4时, num - 1 = 0,一直是合法的。显然x[4]的1,可以通过u[2]的1不断左移得到)
[代码写的太丑,一会放个写得简洁的]
code: