Segments POJ

Segments

题目链接：https://vjudge.net/problem/POJ-3304

题目：

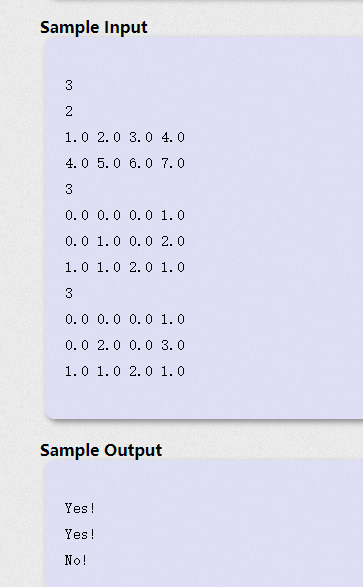
题意：问是否存在一条直线，使所有线段到这条直线的投影至少有一个交点。

思路：就是看有没有一条直线与所有的线段相交，由于数据很小，因此可以暴力求解，将题目给的所有点用结构体存起来，然后任意两个端点相连为一条直线，判断该直线是否与所有的线段相交即可，在设定为直线前先判断该两点之间距离是否小于1e-8，若小于则可以看作为一点，不可组成直线，继续与其他点成为直线，暴力判断。

// 
// Created by HJYL on 2020/1/12.
//
#include<stdio.h>
#include<math.h>
#include<string.h>

#define eps 1e-8
#define pi  3.141592653589793
const int maxn=1e5+10;

using namespace std;

struct Point{
    double x,y;
    Point(double a=0,double b=0){x=a;y=b;}
};

typedef Point Vector;

struct Line{
    double a,b,c,angle;
    Point p1,p2;
    Line(Point s,Point e)
    {
        a=s.y-e.y;
        b=e.x-s.x;
        c=s.x*e.y-e.x*s.y;
        angle=atan2(e.y-s.y,e.x-s.x);
        p1=s;p2=e;
    }
    Line(){}
};

struct Segment
{
    Point s,e;
    Segment(Point a,Point b){s=a;e=b;}
    Segment(double x1,double y1,double x2,double y2)
    {
        s=Point(x1,y1);
        e=Point(x2,y2);
    }
    Segment(){}
};

Vector operator + (Point a,Point b)
{
    return Vector(a.x+b.x,a.y+b.y);
}

Vector operator - (Point a,Point b)
{
    return Vector(a.x-b.x,a.y-b.y);
}

Vector operator * (Point a,double k)
{
    return Vector(a.x*k,a.y*k);
}

Vector operator / (Point a,double k)
{
    return Vector(a.x/k,a.y/k);
}

double Cross(Point &sp, Point &ep, Point &op)
{
    return (sp.x-op.x)*(ep.y-op.y)-(ep.x-op.x)*(sp.y-op.y);
}

double Cross(Vector a,Vector b)
{
    return a.x*b.y-b.x*a.y;
}

int epssgn(double x)
{
    if(fabs(x)<eps)
        return 0;
    else
        return x<0?-1:1;
}

double dis(Point a,Point b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

int IsLineIntersectSegment(Point p1,Point p2,Point s,Point e)
{
    if (Cross(p1,p2,s)*Cross(p1,p2,e)>eps) return 0;
    else return 1;
}

int main()
{
    //freopen("text","r",stdin);
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        scanf("%d",&n);
        Point ll[maxn];
        double xx,yy,xx1,yy1;
        int pos=0;
        for(int i=0;i<n;i++)
        {
            scanf("%lf%lf%lf%lf",&xx,&yy,&xx1,&yy1);
            ll[pos].x=xx;ll[pos].y=yy;
            pos++;
            ll[pos].x=xx1;ll[pos].y=yy1;
            pos++;
        }
        if(n==1||n==2)
            printf("Yes!
");
        else {
            bool ff=false;
            for (int i = 0; i < pos; i++) {
                for (int j = 0; j < pos; j++) {
                    if (i == j)
                        continue;
                    if (dis(ll[i], ll[j]) < eps)
                        continue;
                    bool flag = false;
                    for (int t = 0; t < n; t++) {
                        if(!IsLineIntersectSegment(ll[i],ll[j],ll[t*2],ll[t*2+1]))
                        {
                            flag=true;
                            break;
                        }
                    }
                    if(!flag)
                    {
                        ff=true;
                        break;
                    }
                }
                if(ff)
                    break;
            }
            if(ff)
                printf("Yes!
");
            else
                printf("No!
");
        }
        }
    return 0;
}