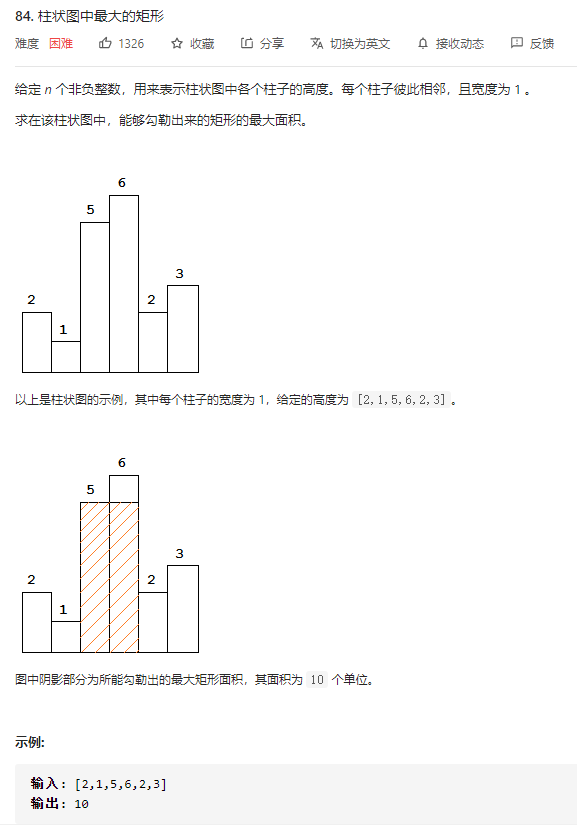
题目描述
方法一——枚举
- 枚举所有高度(矩形)
- 当前矩形能围成的最大面积,取决于向左右扩展时,高度小于当前高度的矩形,记录下左右当前左右坐标,((right - left) -1)* heights[i] 就是当前矩形能围成的最大面积
暴力枚举:枚举所有宽度,时间复杂度为O(n^2)
int largestRectangleArea(vector<int>& heights) {
int len = heights.size();
int ans = 0;
//枚举左边界
for(int i = 0;i < len;i++){
int minHeight = INT_MAX;
for(int j = i;j < len;j++){ //枚举右边界
minHeight = min(minHeight,heights[j]); //高度取决于矮的一端
ans = max(ans, (j - i + 1) * minHeight); //记录最大面积
}
}
return ans;
}
暴力枚举:枚举所有高度,时间复杂度O(n^2)
int largestRectangleArea(vector<int>& heights){
int len = heights.size();
int ans = 0;
for(int i = 0;i < len;i++){
int left = i;
int right = i;
int height = heights[i]; //固定高度
//向左扩展边界,找左边大于当前柱子高度并且最远的索引
while(left - 1 >= 0 && heights[left - 1] >= height){
left--;
}
//向右扩展边界,找右边大于当前柱子高度并且最远的索引
while(right + 1 < len && heights[right + 1] >= height){
right++;
}
//计算当前高度可围成的最大面积
ans = max(ans,(right-left+1) * height);
}
return ans;
}
方法二——分治法
最大的矩形面积出现只会有以下三种情况
- 高度最小的柱子能围成的最大面积
- 最大面积出现在高度最小的柱子左边
- 最大面积出现在高度最小的柱子右边
int calculateArea(vector<int>& heights,int start,int end){
if(start > end){
return 0;
}
int minWidth = heights[start];
int cur = 0;
for(int i = start+1;i <= end;i++){
if(heights[i] < minWidth){
minWidth = heights[i];
cur = i;
}
}
int AreaValue = (end-start + 1) * minWidth;
int leftAreaValue = calculateArea(heights,start,cur-1);
int rightAreaValue = calculateArea(heights,cur+1,end);
return max(max(AreaValue,leftAreaValue),rightAreaValue);
}
int largestRectangleArea(vector<int>& heights){
return calculateArea(heights,0,heights.size()-1);
}
方法三——单调栈
前面三种方法都超时,考虑优化时间复杂度。单调栈的解法与枚举高度类似,要使得当前高度能围成的矩形面积最大,需要向左右扩展能够到达的最大边界,因此我们需要维护一个单调递增的栈(栈中存放柱子的下标),当遍历到的柱子高度不满足单调递增时(大于栈顶柱子高度)说明它是栈顶柱子作为高度的右边界,左边界为栈顶元素的下一个元素,此时可以求出每个柱子作为高度时的最大面积,记录最大面积
- 定义一个栈用于存放所有柱子的下标
- 原数组首添0:便于计算左边界(避免对空栈处理),原数组末尾添0:使得栈中所有元素都能出栈(所有柱子高度能围成的最大面积都能求得)
- 遍历数组,不满足单调递增时,说明栈顶柱子找到了右边界,栈顶柱子位置出栈,它的前一个位置(现在的栈顶元素就是它的左边界),计算宽度,右边界-左边界-1
- 满足单调递增的柱子下标入栈
- 直到遍历完柱子数组
int largestRectangleArea(vector<int>& heights){
int ans = 0;
stack<int> st;
heights.insert(heights.begin(), 0); //减少栈空的判断
heights.push_back(0); //使得前面所有元素都能出栈
for (int i = 0; i < heights.size(); i++){
while (!st.empty() && heights[st.top()] > heights[i]){
int cur = heights[st.top()]; //当前高度
st.pop();
ans = max(ans, (i - st.top() - 1) * cur); //左边界:st.top() 右边界i 在计算宽度的时候需要减1
}
st.push(i);
}
return ans;
}