DLX专题总结

其实我个人非常喜欢DLX.

因为我认为他较为简单——建模 + DLX = AC!

这里先分享一套我较为常用的模板：

const int N = 9;
const int maxn = N*N*N + 10;
const int maxnode=maxn*4+maxn+10;
const int INF=0x3f3f3f3f;

struct DLX{
    #define FF(i,A,S) for(int i = A[S];i != S;i = A[i])
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];//每个点的左右上下指针，所在行列
    int sz,col[maxnode],row[maxnode],S[maxn],H[maxn];//H每行的头结点,S每列的节点数
    int ans[maxn],cnt;
    int out[maxn];
    int n,m;

    void init(int _n,int _m) {
        n=_n, m=_m;
        for(int i = 0;i <= m;i ++)
            S[i]=0,U[i]=D[i]=i,L[i]=i-1,R[i]=i+1;
        R[m] = 0, L[0] = sz = m;
        for(int i = 1;i <= n; ++i) H[i] = -1;
    }

    void link(int r,int c) {
        ++S[col[++sz]=c], row[sz] = r;
        D[sz] = D[c], U[D[c]] = sz;
        U[sz] = c, D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else R[sz]=R[H[r]], L[R[H[r]]]=sz,L[sz]= H[r],R[H[r]] = sz;
    }
    void del(int c){//精确覆盖,删除涉及C列的集合
        L[R[c]]=L[c],R[L[c]]=R[c];
        FF(i,D,c)FF(j,R,i)U[D[j]]=U[j],D[U[j]]=D[j],--S[col[j]];
    }
    void add(int c){  //精确覆盖,恢复涉及C列的集合
        R[L[c]]=L[R[c]]=c;
        FF(i,U,c)FF(j,L,i)++S[col[U[D[j]]=D[U[j]]=j]];
    }
    bool dance(int k){//精确覆盖
        //(剪枝)if(cnt != -1 && cnt <= d) return 0;//精确匹配输出最小
        if(!R[0]){
            //cnt=min(cnt,k);//精确匹配输出最小
            for(int i = 0;i < k; ++i)
                out[(ans[i]-1)/N]=(ans[i]-1)%N+1; //数独输出
            cnt=k;
            return 1;
        }
        int c=R[0];FF(i,R,0)if(S[c]>S[i])c=i;
        del(c);
        FF(i,D,c){
            FF(j,R,i)del(col[j]);
            ans[k]=row[i];
            if(dance(k+1))return 1;
            //dance(k+1);//精确匹配输出最小
            FF(j,L,i)add(col[j]);
        }
        add(c);
        return 0;
    }
    void remove(int c){//重复覆盖
        FF(i,D,c)L[R[i]]=L[i],R[L[i]]=R[i];
    }
     void resume(int c){//重复覆盖
         FF(i,U,c)L[R[i]]=R[L[i]]=i;
    }
    int A(){//估价函数
        int res=0;
        bool vis[m+1];
        memset(vis,0,sizeof(vis));
        FF(i,R,0)if(!vis[i]){
                res++,vis[i]=1;
                FF(j,D,i)FF(k,R,j)vis[col[k]]=1;
            }
        return res;
    }
    void dance(int now,int &ans){//重复覆盖,需要传入一个接收答案的ans
        if(R[0]==0)ans=min(ans,now);
        else if (now+A()>=limit) return ;
        else if(now+A()<ans){
            int temp=INF,c;
            FF(i,R,0)if(temp>S[i])temp=S[i],c=i;
            FF(i,D,c){
                remove(i);
                FF(j,R,i)remove(j);
                dance(now+1,ans);
                FF(j,L,i)resume(j);
                resume(i);
            }
        }
    }
}dlx;

具体的原理我就不再说了，毕竟网上已经有很多优秀的博客。（其实就是我也不是很懂原理，就知道十字交叉链表

这里主要是为了给我刷的kuangbin专题写个总结。顺便写写我个人对DLX的理解吧。

（优化其实都在我给的板子里有所体现，这里就不说了）

DLX最难的地方就是建模了。首先我们需要弄明白行跟列分别代表了什么：

行——所有的发生情况　　列——所有限制条件

就拿三阶数独来举例吧。（POJ - 3074）

首先一个三阶数独，总共有81个格子。每个格子都可以摆上1-9。

所以，所有的发生情况就是9 x 81 = 729 也就是行数了。

 

之后一个三阶数独有4个大的限制条件：

一、所有的格子上必须都有数字摆放（81个格子）

二、每一行上都要恰好有1-9这就个数字 （9行 X 9个数字 = 81）

三、每一列上都要恰好有1-9这就个数字  （9列 X 9个数字 = 81）

四、每一个宫里面都要恰好有1-9这就个数字  （9宫 X 9个数字 = 81）

所以，所有的限制条件就有 （81 + 81 + 81 +81 ）种， 也就是列数了

（这里放一张网上嫖来的图方便理解）

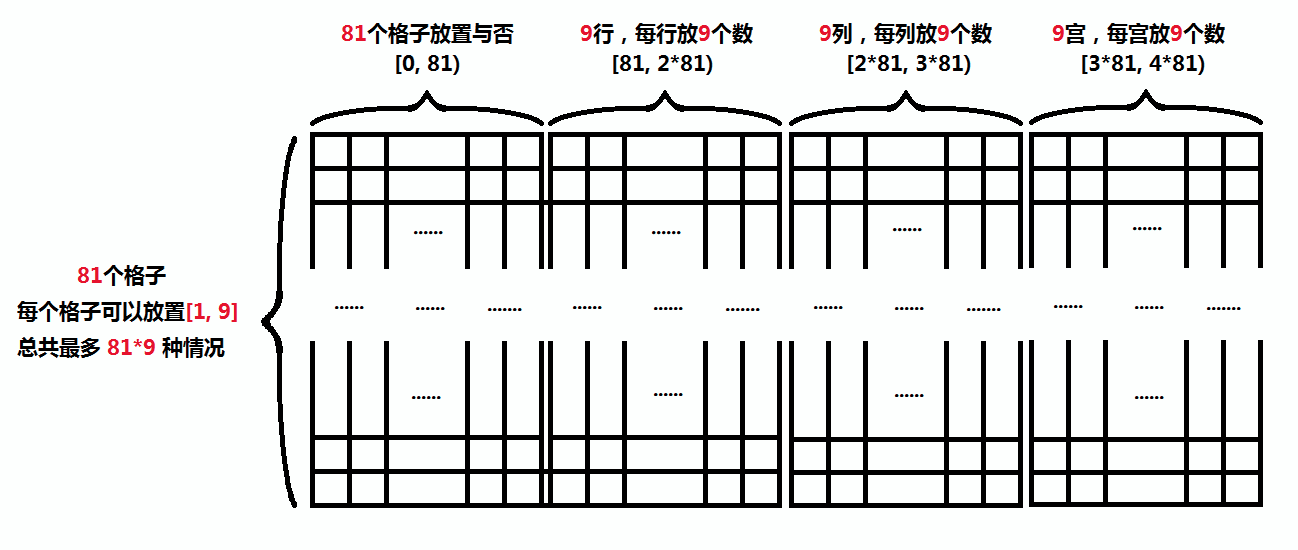
之后解题思路就是，根据题目给出的数据，遍历矩阵里的每一个数字。

分为两种情况：

一、如果是题目给出的数字1-9

(仅仅将这个情况LINK)

　　LINK(行, 格子限制), LINK(行, 行限制), LINK(行, 列限制), LINK(行, 宫限制);

二、如果是0

(枚举每个数字在这个格子里的情况，将其LINK)

　　for (int i = 1;i <= 9; ++i)

　　　　LINK(行, 格子限制), LINK(行, 行限制), LINK(行, 列限制), LINK(行, 宫限制);

之后DANCE就完事儿了。输出的话就是存的时候的行号处理一下输出就行。

这里给出这道题的代码：

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long ll;

const int N = 9;
const int maxn = N*N*N + 10;
const int maxnode=maxn*4+maxn+10;
const int INF=0x3f3f3f3f;
char g[maxn];

inline void read(int &sum) {
    char ch = getchar();
    int tf = 0;
    sum= 0;
    while((ch < '0' || ch > '9') && (ch != '-')) ch = getchar();
    tf=((ch == '-') && (ch=getchar()));
    while(ch>='0' && ch<='9') sum=sum*10+(ch-48),ch=getchar();
    (tf) && (sum =- sum);
}

struct DLX{
    #define FF(i,A,S) for(int i = A[S];i != S;i = A[i])
//    #define maxnode 50000
//    #define maxn 750
//    #define maxm 750
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];//每个点的左右上下指针，所在行列
    int sz,col[maxnode],row[maxnode],S[maxn],H[maxn];//H每行的头结点,S每列的节点数
    int ans[maxn],cnt;
    int out[maxn];
    int n,m;

    void init(int _n,int _m) {
        n=_n, m=_m;
        for(int i = 0;i <= m;i ++)
            S[i]=0,U[i]=D[i]=i,L[i]=i-1,R[i]=i+1;
        R[m] = 0, L[0] = sz = m;
        for(int i = 1;i <= n; ++i) H[i] = -1;
    }

    void link(int r,int c) {
        ++S[col[++sz]=c], row[sz] = r;
        D[sz] = D[c], U[D[c]] = sz;
        U[sz] = c, D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else R[sz]=R[H[r]], L[R[H[r]]]=sz,L[sz]= H[r],R[H[r]] = sz;
    }
    void del(int c){//精确覆盖,删除涉及C列的集合
        L[R[c]]=L[c],R[L[c]]=R[c];
        FF(i,D,c)FF(j,R,i)U[D[j]]=U[j],D[U[j]]=D[j],--S[col[j]];
    }
    void add(int c){  //精确覆盖,恢复涉及C列的集合
        R[L[c]]=L[R[c]]=c;
        FF(i,U,c)FF(j,L,i)++S[col[U[D[j]]=D[U[j]]=j]];
    }
    bool dance(int k){//精确覆盖
        //(剪枝)if(cnt != -1 && cnt <= d) return 0;//精确匹配输出最小
        if(!R[0]){
            //cnt=min(cnt,k);//精确匹配输出最小
            for(int i = 0;i < k; ++i)
                out[(ans[i]-1)/9]=(ans[i]-1)%9+1;
            cnt=k;
            output();
            return 1;
        }
        int c=R[0];FF(i,R,0)if(S[c]>S[i])c=i;
        del(c);
        FF(i,D,c){
            FF(j,R,i)del(col[j]);
            ans[k]=row[i];
            if(dance(k+1))return 1;
            //dance(k+1);//精确匹配输出最小
            FF(j,L,i)add(col[j]);
        }
        add(c);
        return 0;
    }
//    void remove(int c){//重复覆盖
//        FF(i,D,c)L[R[i]]=L[i],R[L[i]]=R[i];
//    }
//     void resume(int c){//重复覆盖
//         FF(i,U,c)L[R[i]]=R[L[i]]=i;
//    }
//    int A(){//估价函数
//        int res=0;
//        bool vis[m+1];
//        memset(vis,0,sizeof(vis));
//        FF(i,R,0)if(!vis[i]){
//                res++,vis[i]=1;
//                FF(j,D,i)FF(k,R,j)vis[col[k]]=1;
//            }
//        return res;
//    }
//    void dance(int now,int &ans){//重复覆盖,需要传入一个接收答案的ans
//        if(R[0]==0)ans=min(ans,now);
//        else if(now+A()<ans){
//            int temp=INF,c;
//            FF(i,R,0)if(temp>S[i])temp=S[i],c=i;
//            FF(i,D,c){
//                remove(i);
//                FF(j,R,i)remove(j);
//                dance(now+1,ans);
//                FF(j,L,i)resume(j);
//                resume(i);
//            }
//        }
//    }
    void output() {
        for (int i = 0; i < cnt; ++i)
            cout << out[i];
        cout << endl;
    }

}dlx;

int main()
{
    while(scanf("%s",g) == 1)
    {
        if(strcmp(g,"end") == 0) break;
        dlx.init(N * N * N,  N * N * 4);
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j)
                for(int k = 1;k <= N;++k)
                    if(g[i * N + j] == '.' || g[i * N + j] == '0' + k)
                    {
                        dlx.link((i*N+j)*N+k, i*N+j+1);
                        dlx.link((i*N+j)*N+k, N*N+i*N+k);
                        dlx.link((i*N+j)*N+k, N*N*2+j*N+k);
                        dlx.link((i*N+j)*N+k, N*N*3+((i/3)*3+(j/3))*N+k);
                    }
        dlx.dance(0);

    }
    return 0;
}

剩下的就都是题目的代码和建模思路了。

先是精确覆盖，这东西非常的快。如果能转换成精确覆盖那么DLX必然是你的最佳选择。

A - Treasure Map ZOJ - 3209

这道题就是很经典的DLX精确覆盖裸题了。

建模思路：

行：所有的拼图数 P

列：所有的面积 N*M（题目要求所有的面积都要被覆盖）

给出代码：

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long ll;

const int INF=0x3f3f3f3f;
int n, m, p;

inline void read(int &sum) {
    char ch = getchar();
    int tf = 0;
    sum= 0;
    while((ch < '0' || ch > '9') && (ch != '-')) ch = getchar();
    tf=((ch == '-') && (ch=getchar()));
    while(ch>='0' && ch<='9') sum=sum*10+(ch-48),ch=getchar();
    (tf) && (sum =- sum);
}

struct DLX{
    #define FF(i,A,s) for(int i = A[s];i != s;i = A[i])
    #define maxnode 500010
    #define maxn 550
    #define maxm 1050
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];//每个点的左右上下指针，所在行列
    int sz,col[maxnode],row[maxnode],s[maxm],H[maxn];//H每行的头结点,s每列的节点数
    int ans[maxm],cnt;

    void init(int m){
        for(int i=0;i<=m;++i)
            L[i]=i-1,R[i]=i+1,U[i]=D[i]=i;
        memset(H,-1,sizeof(H)),memset(s,0,sizeof(s));
        L[0]=m,R[m]=0,sz=m+1;
        cnt = INF;
    }
        void link(int r,int c)
    {
        ++ s[col[++ sz] = c];
        row[sz] = r;
        D[sz] = D[c];
        U[D[c]] = sz;
        U[sz] = c;
        D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else
        {
            R[sz] = R[H[r]];
            L[R[H[r]]] = sz;
            L[sz] = H[r];
            R[H[r]] = sz;
        }
    }
    void del(int c){//精确覆盖,删除涉及C列的集合
        L[R[c]]=L[c],R[L[c]]=R[c];
        FF(i,D,c)FF(j,R,i)U[D[j]]=U[j],D[U[j]]=D[j],--s[col[j]];
    }
    void add(int c){  //精确覆盖,恢复涉及C列的集合
        R[L[c]]=L[R[c]]=c;
        FF(i,U,c)FF(j,L,i)++s[col[U[D[j]]=D[U[j]]=j]];
    }
    bool dance(int k){//精确覆盖
        //if (cnt != -1)
        if(!R[0]){
            cnt=min(k, cnt);return 1;
        }
        int c=R[0];FF(i,R,0)if(s[c]>s[i])c=i;
        del(c);
        FF(i,D,c){
            FF(j,R,i)del(col[j]);
            ans[k]=row[i];
            dance(k+1);
            FF(j,L,i)add(col[j]);
        }
        add(c);
        return 0;
    }
    void remove(int c){//重复覆盖
        FF(i,D,c)L[R[i]]=L[i],R[L[i]]=R[i];
    }
     void resume(int c){//重复覆盖
         FF(i,U,c)L[R[i]]=R[L[i]]=i;
     }
    int A(){//估价函数
        int res=0;
        bool vis[m+1];
        memset(vis,0,sizeof(vis));
        FF(i,R,0)if(!vis[i]){
                res++,vis[i]=1;
                FF(j,D,i)FF(k,R,j)vis[col[k]]=1;
            }
        return res;
    }
    void dance(int now,int &ans){//重复覆盖,需要传入一个接收答案的ans
        if(R[0]==0)ans=min(ans,now);
        else if(now+A()<ans){
            int temp=INF,c;
            FF(i,R,0)if(temp>s[i])temp=s[i],c=i;
            FF(i,D,c){
                remove(i); FF(j,R,i)remove(j);
                dance(now+1,ans);
                FF(j,L,i)resume(j); resume(i);
            }
        }
    }
    void output() {
//        for (int i = 0; i < cnt; ++i)
//            cout <<ans[i]<< ((i==cnt-1)?"
":" ");
        cout << cnt << endl;
    }
}dlx;

int main(){
    int T; read(T);
    while (T--) {
        read(n), read(m), read(p);
        dlx.init(n*m);
        int x1,x2,y1,y2;
        for (int i = 1; i <= p; ++i){
            read(x1),read(y1),read(x2),read(y2);
            for (int x = x1+1; x<= x2; ++x)
                for (int y = y1+1; y <= y2; ++y)
                    dlx.link(i, y+(x-1)*m);
        }
        dlx.dance(0);
        cout << ((dlx.cnt==INF)?-1:dlx.cnt)<< endl;
    }
    return 0;
}

 

B - Easy Finding POJ - 3740

这道题就不讲了太裸了

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long ll;

const int INF=0x3f3f3f3f;
int n, m;

inline bool read(int &sum) {
    char ch = getchar();
    int tf = 0;
    sum = 0;
    while((ch < '0' || ch > '9') && (ch != '-')) ch = getchar();
    tf = ((ch == '-') && (ch = getchar()));
    while(ch >= '0' && ch <= '9') sum = sum * 10+ (ch - 48), ch = getchar();
    (tf) && (sum =- sum);
    return 1;
}

struct DLX{
    #define FF(i,A,s) for(int i = A[s];i != s;i = A[i])
    #define maxn 6305
    int L[maxn],R[maxn],U[maxn],D[maxn];//每个点的左右上下指针，所在行列
    int sz,col[maxn],row[maxn],s[maxn],H[maxn];//H每行的头结点,s每列的节点数
    int ans[maxn],cnt;

    void init(int m){
        for(int i=0;i<=m;++i)
            L[i]=i-1,R[i]=i+1,U[i]=D[i]=i;
        memset(H,-1,sizeof(H)),memset(s,0,sizeof(s));
        L[0]=m,R[m]=0,sz=m+1;
    }
        void link(int r,int c)
    {
        ++ s[col[++ sz] = c];
        row[sz] = r;
        D[sz] = D[c];
        U[D[c]] = sz;
        U[sz] = c;
        D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else
        {
            R[sz] = R[H[r]];
            L[R[H[r]]] = sz;
            L[sz] = H[r];
            R[H[r]] = sz;
        }
    }

    void del(int c){//精确覆盖,删除涉及C列的集合
        L[R[c]]=L[c],R[L[c]]=R[c];
        FF(i,D,c)FF(j,R,i)U[D[j]]=U[j],D[U[j]]=D[j],--s[col[j]];
    }
    void add(int c){  //精确覆盖,恢复涉及C列的集合
        R[L[c]]=L[R[c]]=c;
        FF(i,U,c)FF(j,L,i)++s[col[U[D[j]]=D[U[j]]=j]];
    }
    bool dance(int k){//精确覆盖
        if(!R[0]){
            cnt=k;return 1;
        }
        int c=R[0];FF(i,R,0)if(s[c]>s[i])c=i;
        del(c);
        FF(i,D,c){
            FF(j,R,i)del(col[j]);
            ans[k]=row[i]; if(dance(k+1))return 1;
            FF(j,L,i)add(col[j]);
        }
        add(c);
        return 0;
    }
    void remove(int c){//重复覆盖
        FF(i,D,c)L[R[i]]=L[i],R[L[i]]=R[i];
    }
     void resume(int c){//重复覆盖
         FF(i,U,c)L[R[i]]=R[L[i]]=i;
     }
//    int A(){//估价函数
//        int res=0;
//        bool vis[m+1];
//        memset(vis,0,sizeof(vis));
//        FF(i,R,0)if(!vis[i]){
//                res++,vis[i]=1;
//                FF(j,D,i)FF(k,R,j)vis[col[k]]=1;
//            }
//        return res;
//    }
//    void dance(int now,int &ans){//重复覆盖,需要传入一个接收答案的ans
//        if(R[0]==0)ans=min(ans,now);
//        else if(now+A()<ans){
//            int temp=INF,c;
//            FF(i,R,0)if(temp>s[i])temp=s[i],c=i;
//            FF(i,D,c){
//                remove(i);
//                FF(j,R,i)remove(j);
//                dance(now+1,ans);
//                FF(j,L,i)resume(j);
//                resume(i);
//            }
//        }
//    }
}dlx;

int main(){
    cin.tie(0);
    ios::sync_with_stdio(0);
    while (cin >> n >> m) {
        dlx.init(m);
        int temp;
        for (int i = 1; i <= n; ++i)
            for (int j = 1; j <= m; ++j) {
                read(temp);
                if (temp) dlx.link(i,j);
            }
        if (dlx.dance(0)) cout << "Yes, I found it" << endl;
        else cout << "It is impossible" << endl;
    }
    return 0;
}

G - Sudoku ZOJ - 3122

这道题就只是四阶数独而已，只是将N改为了16。

建模的思路与之前的3阶数独是一样的。就不讲了（注意这里有些OJ的题面给的样例是错的，可以使用我注释里的）

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef long long ll;

const int N = 16;
const int maxn = N*N*N + 10;
const int maxnode=maxn*4+maxn+10;
const int INF=0x3f3f3f3f;
string g;


struct DLX{
    #define FF(i,A,S) for(int i = A[S];i != S;i = A[i])
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];//每个点的左右上下指针，所在行列
    int sz,col[maxnode],row[maxnode],S[maxn],H[maxn];//H每行的头结点,S每列的节点数
    int ans[maxn],cnt;
    int out[maxn];
    int n,m;

    void init(int _n,int _m) {
        n=_n, m=_m;
        for(int i = 0;i <= m;i ++)
            S[i]=0,U[i]=D[i]=i,L[i]=i-1,R[i]=i+1;
        R[m] = 0, L[0] = sz = m;
        for(int i = 1;i <= n; ++i) H[i] = -1;
    }

    void link(int r,int c) {
        ++S[col[++sz]=c], row[sz] = r;
        D[sz] = D[c], U[D[c]] = sz;
        U[sz] = c, D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else R[sz]=R[H[r]], L[R[H[r]]]=sz,L[sz]= H[r],R[H[r]] = sz;
    }
    void del(int c){//精确覆盖,删除涉及C列的集合
        L[R[c]]=L[c],R[L[c]]=R[c];
        FF(i,D,c)FF(j,R,i)U[D[j]]=U[j],D[U[j]]=D[j],--S[col[j]];
    }
    void add(int c){  //精确覆盖,恢复涉及C列的集合
        R[L[c]]=L[R[c]]=c;
        FF(i,U,c)FF(j,L,i)++S[col[U[D[j]]=D[U[j]]=j]];
    }
    bool dance(int k){//精确覆盖
        //(剪枝)if(cnt != -1 && cnt <= d) return 0;//精确匹配输出最小
        if(!R[0]){
            //cnt=min(cnt,k);//精确匹配输出最小
            for(int i = 0;i < k; ++i)
                out[(ans[i]-1)/16]=(ans[i]-1)%16+1;
            cnt=k;
            output();
            return 1;
        }
        int c=R[0];FF(i,R,0)if(S[c]>S[i])c=i;
        del(c);
        FF(i,D,c){
            FF(j,R,i)del(col[j]);
            ans[k]=row[i];
            if(dance(k+1))return 1;
            //dance(k+1);//精确匹配输出最小
            FF(j,L,i)add(col[j]);
        }
        add(c);
        return 0;
    }
    void output() {
        for (int i = 0; i < cnt; ++i) {
            cout << (char)(out[i]-1+'A');
            if ((i+1)%16==0) cout << endl;
        }
    }
}dlx;

int main() {
    string temp; int cnt = -1;
    while (cin >> temp) {
        g.clear(), g += temp;
        for (int i = 1; i < 16; ++i) cin >> temp, g += temp;
        dlx.init(N * N * N,  N * N * 4);
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j)
                for(int k = 1; k <= N;++k) {
                    if(g[i * N+j] == '-' || g[i * N + j] == 'A'+k-1) {
                        dlx.link((i*N+j)*N+k, i*N+j+1);
                        dlx.link((i*N+j)*N+k, N*N+i*N+k);
                        dlx.link((i*N+j)*N+k, N*N*2+j*N+k);
                        dlx.link((i*N+j)*N+k, N*N*3+((i/4)*4+(j/4))*N+k);
                    }
                }
        if (++cnt) cout << endl;
        dlx.dance(0);
    }

    return 0;
}

/*
--A----C-----O-I
-J--A-B-P-CGF-H-
--D--F-I-E----P-
-G-EL-H----M-J--
----E----C--G---
-I--K-GA-B---E-J
D-GP--J-F----A--
-E---C-B--DP--O-
E--F-M--D--L-K-A
-C--------O-I-L-
H-P-C--F-A--B---
---G-OD---J----H
K---J----H-A-P-L
--B--P--E--K--A-
-H--B--K--FI-C--
--F---C--D--H-N-
*/

H - Squiggly Sudoku HDU - 4069

这道题倒是挺有趣的，难的地方在他的宫的构建（虽然也不难

我的想法是先BFS预处理一遍每个的宫，并将其标号，并将宫里的格子用宫号标记

之后就是常规数独的做法——LINK(行, 格子限制), LINK(行, 行限制), LINK(行, 列限制), LINK(行, 格子对应的宫号限制);

之后就看我的代码吧。

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
using namespace std;
typedef long long ll;

const int N = 9;
const int maxn = N*N*N + 10;
const int maxnode=maxn*4+maxn+10;
const int INF=0x3f3f3f3f;
int g[N][N];
int wall[N][N][4];//用于标记墙
int id[N][N];   //用于划分宫
int dic[4][2]={0,-1, 1,0, 0,1, -1,0};
int gong_id;
int res[N*N]; //用于最后输出

struct DLX{
    #define FF(i,A,S) for(int i = A[S];i != S;i = A[i])
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];//每个点的左右上下指针，所在行列
    int sz,col[maxnode],row[maxnode],S[maxn],H[maxn];//H每行的头结点,S每列的节点数
    int ans[maxn],cnt;
    int out[maxn];
    int n,m;

    void init(int _n,int _m) {
        n=_n, m=_m, cnt=0;
        for(int i = 0;i <= m;i ++)
            S[i]=0,U[i]=D[i]=i,L[i]=i-1,R[i]=i+1;
        R[m] = 0, L[0] = sz = m;
        for(int i = 1;i <= n; ++i) H[i] = -1;
    }

    void link(int r,int c) {
        ++S[col[++sz]=c], row[sz] = r;
        D[sz] = D[c], U[D[c]] = sz;
        U[sz] = c, D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else R[sz]=R[H[r]], L[R[H[r]]]=sz,L[sz]= H[r],R[H[r]] = sz;
    }
    void del(int c){//精确覆盖,删除涉及C列的集合
        L[R[c]]=L[c],R[L[c]]=R[c];
        FF(i,D,c)FF(j,R,i)U[D[j]]=U[j],D[U[j]]=D[j],--S[col[j]];
    }
    void add(int c){  //精确覆盖,恢复涉及C列的集合
        R[L[c]]=L[R[c]]=c;
        FF(i,U,c)FF(j,L,i)++S[col[U[D[j]]=D[U[j]]=j]];
    }
    int dance(int k){//精确覆盖
        //(剪枝)if(cnt != -1 && cnt <= d) return 0;//精确匹配输出最小
        if(!R[0]){
            //cnt=min(cnt,k);//精确匹配输出最小
            for(int i = 0; i < k; ++i)
                out[(ans[i]-1)/N]=(ans[i]-1)%N+1;
            ++cnt, memcpy(res, out, sizeof(res));
            if (cnt > 1) return -1;
        }
        int c=R[0];FF(i,R,0)if(S[c]>S[i])c=i;
        del(c);
        FF(i,D,c){
            FF(j,R,i)del(col[j]);
            ans[k]=row[i];
            if (dance(k+1)==-1) return -1;
            //dance(k+1);//精确匹配输出最小
            FF(j,L,i)add(col[j]);
        }
        add(c);
        if (cnt > 1) return -1;
        return 0;
    }
}dlx;

void BFS(int x, int y) {
    queue<pair<int, int> > q;
    q.push({x,y}), id[x][y] = ++gong_id;
    while (!q.empty()) {
        pair<int, int> top = q.front(); q.pop();
        for (int i = 0; i < 4; ++i) {
            int tx = top.first + dic[i][0];
            int ty = top.second + dic[i][1];
            if (wall[top.first][top.second][i] || id[tx][ty]) continue;
            id[tx][ty] = gong_id, q.push({tx,ty});
        }
    }
}

int main() {
    int T; cin >> T;
    for (int z = 1; z <= T; ++z) {
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j) {
                cin >> g[i][j],
                wall[i][j][0] = wall[i][j][1] = wall[i][j][2] = wall[i][j][3] = id[i][j] = 0;
                if (g[i][j] >= 128) g[i][j] -= 128, wall[i][j][0]=1; //left
                if (g[i][j] >= 64) g[i][j] -= 64, wall[i][j][1]=1;  //down
                if (g[i][j] >= 32) g[i][j] -= 32, wall[i][j][2]=1;  //right
                if (g[i][j] >= 16) g[i][j] -= 16, wall[i][j][3]=1;  //up
        }

        gong_id = 0;
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j)
                if (!id[i][j]) BFS(i,j);

        dlx.init(N * N * N,  N * N * 4);
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j)
                for(int k = 1; k <= N;++k) {
                    if(g[i][j] == 0 || g[i][j] == k) {
                        dlx.link((i*N+j)*N+k, i*N+j+1);
                        dlx.link((i*N+j)*N+k, N*N+i*N+k);
                        dlx.link((i*N+j)*N+k, N*N*2+j*N+k);
                        dlx.link((i*N+j)*N+k, N*N*3+(id[i][j]-1)*N+k);
                    }
                }
        cout << "Case "<< z << ":" << endl;
        if (dlx.dance(0) == -1)  cout << "Multiple Solutions" << endl;
        else if (dlx.cnt)
            for (int i = 0; i < N*N; ++i) {
                cout << res[i];
                if ((i+1)%N==0) cout << endl;
            }
        else cout << "No solution" << endl;
    }
    return 0;
}

之后是重复覆盖，这东西非常玄学。我有几次都会超时，有几次又不超。

重复覆盖剪枝非常的重要，如果不剪枝就相当于是暴力回溯，这样的话他的解空间就会非常的大。必然会超时。

但是说到剪枝，我所遇到的也就只是A()优化而已。

D - 神龙的难题 FZU - 1686

建模思路：

行：(N-K+1)*(M-K+1) 所有可以被喷格子数

列：所有的敌人数（因为所有的敌人都要被覆盖）

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
using namespace std;
typedef long long ll;

const int N = 9;
const int maxn = N*N*N + 10;
const int maxnode=maxn*4+maxn+10;
const int INF=0x3f3f3f3f;
int g[N][N];
int wall[N][N][4];//用于标记墙
int id[N][N];   //用于划分宫
int dic[4][2]={0,-1, 1,0, 0,1, -1,0};
int gong_id;
int res[N*N]; //用于最后输出

struct DLX{
    #define FF(i,A,S) for(int i = A[S];i != S;i = A[i])
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];//每个点的左右上下指针，所在行列
    int sz,col[maxnode],row[maxnode],S[maxn],H[maxn];//H每行的头结点,S每列的节点数
    int ans[maxn],cnt;
    int out[maxn];
    int n,m;

    void init(int _n,int _m) {
        n=_n, m=_m, cnt=0;
        for(int i = 0;i <= m;i ++)
            S[i]=0,U[i]=D[i]=i,L[i]=i-1,R[i]=i+1;
        R[m] = 0, L[0] = sz = m;
        for(int i = 1;i <= n; ++i) H[i] = -1;
    }

    void link(int r,int c) {
        ++S[col[++sz]=c], row[sz] = r;
        D[sz] = D[c], U[D[c]] = sz;
        U[sz] = c, D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else R[sz]=R[H[r]], L[R[H[r]]]=sz,L[sz]= H[r],R[H[r]] = sz;
    }
    void del(int c){//精确覆盖,删除涉及C列的集合
        L[R[c]]=L[c],R[L[c]]=R[c];
        FF(i,D,c)FF(j,R,i)U[D[j]]=U[j],D[U[j]]=D[j],--S[col[j]];
    }
    void add(int c){  //精确覆盖,恢复涉及C列的集合
        R[L[c]]=L[R[c]]=c;
        FF(i,U,c)FF(j,L,i)++S[col[U[D[j]]=D[U[j]]=j]];
    }
    int dance(int k){//精确覆盖
        //(剪枝)if(cnt != -1 && cnt <= d) return 0;//精确匹配输出最小
        if(!R[0]){
            //cnt=min(cnt,k);//精确匹配输出最小
            for(int i = 0; i < k; ++i)
                out[(ans[i]-1)/N]=(ans[i]-1)%N+1;
            ++cnt, memcpy(res, out, sizeof(res));
            if (cnt > 1) return -1;
        }
        int c=R[0];FF(i,R,0)if(S[c]>S[i])c=i;
        del(c);
        FF(i,D,c){
            FF(j,R,i)del(col[j]);
            ans[k]=row[i];
            if (dance(k+1)==-1) return -1;
            //dance(k+1);//精确匹配输出最小
            FF(j,L,i)add(col[j]);
        }
        add(c);
        if (cnt > 1) return -1;
        return 0;
    }
}dlx;

void BFS(int x, int y) {
    queue<pair<int, int> > q;
    q.push({x,y}), id[x][y] = ++gong_id;
    while (!q.empty()) {
        pair<int, int> top = q.front(); q.pop();
        for (int i = 0; i < 4; ++i) {
            int tx = top.first + dic[i][0];
            int ty = top.second + dic[i][1];
            if (wall[top.first][top.second][i] || id[tx][ty]) continue;
            id[tx][ty] = gong_id, q.push({tx,ty});
        }
    }
}

int main() {
    int T; cin >> T;
    for (int z = 1; z <= T; ++z) {
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j) {
                cin >> g[i][j],
                wall[i][j][0] = wall[i][j][1] = wall[i][j][2] = wall[i][j][3] = id[i][j] = 0;
                if (g[i][j] >= 128) g[i][j] -= 128, wall[i][j][0]=1; //left
                if (g[i][j] >= 64) g[i][j] -= 64, wall[i][j][1]=1;  //down
                if (g[i][j] >= 32) g[i][j] -= 32, wall[i][j][2]=1;  //right
                if (g[i][j] >= 16) g[i][j] -= 16, wall[i][j][3]=1;  //up
        }

        gong_id = 0;
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j)
                if (!id[i][j]) BFS(i,j);

        dlx.init(N * N * N,  N * N * 4);
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j)
                for(int k = 1; k <= N;++k) {
                    if(g[i][j] == 0 || g[i][j] == k) {
                        dlx.link((i*N+j)*N+k, i*N+j+1);
                        dlx.link((i*N+j)*N+k, N*N+i*N+k);
                        dlx.link((i*N+j)*N+k, N*N*2+j*N+k);
                        dlx.link((i*N+j)*N+k, N*N*3+(id[i][j]-1)*N+k);
                    }
                }
        cout << "Case "<< z << ":" << endl;
        if (dlx.dance(0) == -1)  cout << "Multiple Solutions" << endl;
        else if (dlx.cnt)
            for (int i = 0; i < N*N; ++i) {
                cout << res[i];
                if ((i+1)%N==0) cout << endl;
            }
        else cout << "No solution" << endl;
    }
    return 0;
}

E - Square Destroyer POJ - 1084

这道题目老恶心了。

给每个规模下的方块标号。首先预处理每个规模下每根火柴对应的方块位置。

（这块代码我是嫖网上的）

建模思路：

行：每根火柴（2*N*(N+1)）

列：所有的方块（N*N + (N-1)*(N-1) + ... 1*1)

但是题目有可能会先拿走几根火柴。这部分就不是很好处理。

网上有些是利用DLX内部的删除函数来删除的，但是我个人是喜欢用hash来写的。（其实就是不懂DLX的原理不会删）

先将给出的火柴标记，并将火柴所对应的方块标记，之后把剩余的方块hash。（那么列数就是后面的hash数）

后面通过hash来Link即可。

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iomanip>
using namespace std;
typedef long long ll;

const int N = 60 + 5;
const int maxn = 1*1+2*2+3*3+4*4+5*5+5;
const int maxnode=maxn*N+10;
const int INF=0x3f3f3f3f;
int n, m;

int match[6][N][maxn];//矩阵大小，火柴标号，对应小框子, //第三级的0是用来记录影响了几个格子的
bool isUsed[maxn];
int hash_col[maxn];
void init()
{
    //总方格边长
    for(int len=1;len<=5;len++)  {
        int cnt=0;
        //小方格大小
        for(int sz=1;sz<=len;sz++)
            //起点横坐标
            for(int i=1;i<=len+1-sz;i++)
            //起点纵坐标
                for(int j=0;j<len+1-sz;j++) {
                    ++cnt;
                    for(int k=0;k<sz;k++) match[len][i+j*(2*len+1)+k][++match[len][i+j*(2*len+1)+k][0]]=cnt;
                    for(int k=0;k<sz;k++) match[len][i+(j+sz)*(2*len+1)+k][++match[len][i+(j+sz)*(2*len+1)+k][0]]=cnt;
                    for(int k=0;k<sz;k++) match[len][i+len+(j+k)*(2*len+1)][++match[len][i+len+(j+k)*(2*len+1)][0]]=cnt;
                    for(int k=0;k<sz;k++) match[len][i+len+sz+(j+k)*(2*len+1)][++match[len][i+len+sz+(j+k)*(2*len+1)][0]]=cnt;
                }
    }
}

struct DLX{
    #define FF(i,A,S) for(int i = A[S];i != S;i = A[i])
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];//每个点的左右上下指针，所在行列
    int sz,col[maxnode],row[maxnode],S[maxn],H[maxn];//H每行的头结点,S每列的节点数
    int ans[maxn],cnt;
    int out[maxn];
    int n,m;

    void init(int _n,int _m) {
        n=_n, m=_m;
        for(int i = 0;i <= m;i ++)
            S[i]=0,U[i]=D[i]=i,L[i]=i-1,R[i]=i+1;
        R[m] = 0, L[0] = sz = m;
        for(int i = 1;i <= n; ++i) H[i] = -1;
    }

    void link(int r,int c) {
        ++S[col[++sz]=c], row[sz] = r;
        D[sz] = D[c], U[D[c]] = sz;
        U[sz] = c, D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else R[sz]=R[H[r]], L[R[H[r]]]=sz,L[sz]= H[r],R[H[r]] = sz;
    }

    void remove(int c){//重复覆盖
        FF(i,D,c)L[R[i]]=L[i],R[L[i]]=R[i];
    }
     void resume(int c){//重复覆盖
         FF(i,U,c)L[R[i]]=R[L[i]]=i;
    }
    int A(){//估价函数
        int res=0;
        bool vis[m+1];
        memset(vis,0,sizeof(vis));
        FF(i,R,0)if(!vis[i]){
                res++,vis[i]=1;
                FF(j,D,i)FF(k,R,j)vis[col[k]]=1;
            }
        return res;
    }
    void dance(int now,int &ans){//重复覆盖,需要传入一个接收答案的ans
        if(R[0]==0) {
            ans=min(ans,now);
            return ;
        }
        else if(now+A()<ans){
            int temp=INF,c;
            FF(i,R,0)if(temp>S[i])temp=S[i],c=i;
            FF(i,D,c){
                remove(i);
                FF(j,R,i)remove(j);
                dance(now+1,ans);
                FF(j,L,i)resume(j);
                resume(i);
            }
        }
    }
}dlx;

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int T; cin >> T;
    init();
    while (T--) {
        cin >>  n >> m;
        memset(isUsed, 0, sizeof(isUsed));
        memset(hash_col, 0, sizeof(hash_col));
        for (int i = 0; i < m; ++i) {
            int temp; cin >> temp;
            for (int j=1; j <= match[n][temp][0]; ++j)
                isUsed[match[n][temp][j]]=1;
        }
        int limit = 0; for (int i = 1; i <= n; ++i) limit += i*i;
        int col = 0;
        for (int i = 1; i <= limit; ++i) if (!isUsed[i]) hash_col[i]=++col;
        dlx.init(2*n*(n+1), col);
        for (int i = 1; i <= 2*n*(n+1); ++i)
            for (int j = 1; j <= match[n][i][0]; ++j)
                if (hash_col[match[n][i][j]])
                    dlx.link(i, hash_col[match[n][i][j]]);
        int ans = INF;
        dlx.dance(0,ans);
        cout << ans << endl;
    }
    return 0;
}

C - Radar HDU - 2295

这道题非常的经典。二分答案+DLXcheck

建模思路：

行：雷达数量 M

列：城市数量 N （每个城市都需要被覆盖）

但是这道题还给了一个K操作员的条件，所以就可以放在A()里剪枝

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iomanip>
using namespace std;
typedef long long ll;

const int N = 50+5;
const int maxn = N*N + 10;
const int maxnode=maxn*N+10;
const int INF=0x3f3f3f3f;
bool g[N][N];
int n, m, k;

struct node {
    int x, y;
     bool operator < (const node& a) const {
        if (x == a.x) return y < a.y;
        return x < a.x;
    }
}r[N],c[N];

struct node1 {
    double val;
    int id;
    bool operator <(const node1& a) const{
        return val < a.val;
    }
};
vector<node1> dist[N];

struct DLX{
    #define FF(i,A,S) for(int i = A[S];i != S;i = A[i])
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];//每个点的左右上下指针，所在行列
    int sz,col[maxnode],row[maxnode],S[maxn],H[maxn];//H每行的头结点,S每列的节点数
    int ans[maxn],cnt;
    int out[maxn];
    int n,m;

    void init(int _n,int _m) {
        n=_n, m=_m;
        for(int i = 0;i <= m;i ++)
            S[i]=0,U[i]=D[i]=i,L[i]=i-1,R[i]=i+1;
        R[m] = 0, L[0] = sz = m;
        for(int i = 1;i <= n; ++i) H[i] = -1;
    }

    void link(int r,int c) {
        ++S[col[++sz]=c], row[sz] = r;
        D[sz] = D[c], U[D[c]] = sz;
        U[sz] = c, D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else R[sz]=R[H[r]], L[R[H[r]]]=sz,L[sz]= H[r],R[H[r]] = sz;
    }

    void remove(int c){//重复覆盖
        FF(i,D,c)L[R[i]]=L[i],R[L[i]]=R[i];
    }
     void resume(int c){//重复覆盖
         FF(i,U,c)L[R[i]]=R[L[i]]=i;
    }
    int A(){//估价函数
        int res=0;
        bool vis[m+1];
        memset(vis,0,sizeof(vis));
        FF(i,R,0)if(!vis[i]){
                res++,vis[i]=1;
                FF(j,D,i)FF(k,R,j)vis[col[k]]=1;
            }
        return res;
    }
    void dance(int now,int &ans){//重复覆盖,需要传入一个接收答案的ans
        if(R[0]==0) {
            ans=min(ans,now);
            return ;
        }
        else if(now+A()> k) return ;
        else if(now+A()<ans){
            int temp=INF,c;
            FF(i,R,0)if(temp>S[i])temp=S[i],c=i;
            FF(i,D,c){
                remove(i);
                FF(j,R,i)remove(j);
                dance(now+1,ans);
                FF(j,L,i)resume(j);
                resume(i);
            }
        }
    }
}dlx;

bool Link(double rad) {
    dlx.init(m, n);
    node1 temp = {rad, 0};
    for (int i = 0; i < m; ++i) {
        int limit = upper_bound(dist[i].begin(), dist[i].end(), temp)-dist[i].begin();
        for (int j = 0; j < limit; ++j)
            dlx.link(i+1, dist[i][j].id+1);
    }
    int ans = INF;
    dlx.dance(0, ans);
    return (ans==INF)?0:1;
}

double cal(double x1, double x2, double y1, double y2) {
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}

int main()
{
    int T; cin >> T;
    while (T--) {
        cin >>  n >> m >> k;
        for (int i = 0; i < n; ++i) cin >> c[i].x >> c[i].y;
        for (int i = 0; i < m; ++i) cin >> r[i].x >> r[i].y;
        for (int i = 0; i < m; ++i) {
            dist[i].clear();
            for (int j = 0; j < n; ++j) {
                dist[i].push_back({cal(r[i].x,c[j].x,r[i].y,c[j].y), j});
            }
            sort(dist[i].begin(), dist[i].end());
//            for (int j = 0; j < n; ++j) cout << " " << dist[i][j].id;
//            cout << endl;
        }

        double L = 0, R = 1e4;
        while (R - L > 1e-8) {
            double MID = (R+L)/2;
            //cout << MID << endl;
            if (Link(MID)) R = MID;
            else L = MID;
        }
        cout << fixed << setprecision(6) << R << endl;
    }
    return 0;
}

K - Airport HDU - 5046

这道题跟上一道差不多。区别就是改成了曼哈顿距离

建模思路：

行：城市数量 N

列：城市数量 N （每个城市都需要被覆盖）

整数二分的姿势别错了

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iomanip>
using namespace std;
typedef long long ll;

const int N = 60+5;
const int maxn = N*N + 10;
const int maxnode=maxn*N+10;
const int INF=0x3f3f3f3f;
int n, k;

struct node {
    ll x, y;
     bool operator < (const node& a) const {
        if (x == a.x) return y < a.y;
        return x < a.x;
    }
}r[N],c[N];

ll dist[N][N];

struct DLX{
    #define FF(i,A,S) for(int i = A[S];i != S;i = A[i])
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];//每个点的左右上下指针，所在行列
    int sz,col[maxnode],row[maxnode],S[maxn],H[maxn];//H每行的头结点,S每列的节点数
    int ans[maxn],cnt;
    int out[maxn];
    int n,m;

    void init(int _n,int _m) {
        n=_n, m=_m;
        for(int i = 0;i <= m;i ++)
            S[i]=0,U[i]=D[i]=i,L[i]=i-1,R[i]=i+1;
        R[m] = 0, L[0] = sz = m;
        for(int i = 1;i <= n; ++i) H[i] = -1;
    }

    void link(int r,int c) {
        ++S[col[++sz]=c], row[sz] = r;
        D[sz] = D[c], U[D[c]] = sz;
        U[sz] = c, D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else R[sz]=R[H[r]], L[R[H[r]]]=sz,L[sz]= H[r],R[H[r]] = sz;
    }

    void remove(int c){//重复覆盖
        FF(i,D,c)L[R[i]]=L[i],R[L[i]]=R[i];
    }
     void resume(int c){//重复覆盖
         FF(i,U,c)L[R[i]]=R[L[i]]=i;
    }
    int A(){//估价函数
        int res=0;
        bool vis[m+1];
        memset(vis,0,sizeof(vis));
        FF(i,R,0)if(!vis[i]){
                res++,vis[i]=1;
                FF(j,D,i)FF(k,R,j)vis[col[k]]=1;
            }
        return res;
    }
    bool dance(int now){//重复覆盖,需要传入一个接收答案的ans
        if(R[0]==0) {
            return 1;
        }
        else if(now+A()<=k){
            int temp=INF,c;
            FF(i,R,0)if(temp>S[i])temp=S[i],c=i;
            FF(i,D,c){
                remove(i);
                FF(j,R,i)remove(j);
                if (dance(now+1)) return 1;
                FF(j,L,i)resume(j);
                resume(i);
            }
        }
        return 0;
    }
}dlx;

ll cal(ll x1, ll x2, ll y1, ll y2) {
    return abs(x1-x2)+abs(y1-y2);
}

int main()
{
    cin.tie(0);
    ios::sync_with_stdio(0);
    int T; cin >> T;
    for (int z = 1; z <= T; ++z) {
        cin >>  n >> k;
        for (int i = 0; i < n; ++i)
            cin >> c[i].x >> c[i].y;

        ll l = 0, r = 100000000000LL;
        ll ans = r;
        while (l <= r) {
            ll mid = (l + r) / 2;
            dlx.init(n, n);
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if (cal(c[i].x, c[j].x, c[i].y, c[j].y) <= mid)
                        dlx.link(i+1, j+1);
                }
            }
            if (dlx.dance(0)) {
                r = mid - 1;
                ans = min(ans, mid);
            }
            else l = mid + 1;
        }
        cout << "Case #" << z << ": " << ans << endl;
    }
    return 0;
}

DLX进阶技巧：

一、用于求最大集合的数量，集合内的数两两满足一个条件

 I - Divisibility

题目大意：求选出两两不能整除的最大个数

解题思路：

做法比较多，本人是在DLX专题里做到所以就用DLX来做了

枚举每两个数，若能相除就 link i 跟 j 代表选择 i 不选择 j

最后把最小重复覆盖改成最大就行了

核心：对题目的图形灵活思考，

这里的所有列被覆盖即代表所有数都不能被选，即两两相除互不为0的一种情况

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1000+5;
const int maxn = 500010;
const int maxnode=maxn+10;
const int INF=0x3f3f3f3f;
int n;

struct DLX{
    #define FF(i,A,S) for(int i = A[S];i != S;i = A[i])
    int L[maxnode],R[maxnode],U[maxnode],D[maxnode];//每个点的左右上下指针，所在行列
    int sz,col[maxnode],row[maxnode],S[maxn],H[maxn];//H每行的头结点,S每列的节点数
    int ans[maxn],cnt;
    int out[maxn];
    int n,m;

    void init(int _n,int _m) {
        n=_n, m=_m;
        for(int i = 0;i <= m;i ++)
            S[i]=0,U[i]=D[i]=i,L[i]=i-1,R[i]=i+1;
        R[m] = 0, L[0] = sz = m;
        for(int i = 1;i <= n; ++i) H[i] = -1;
    }

    void link(int r,int c) {
        ++S[col[++sz]=c], row[sz] = r;
        D[sz] = D[c], U[D[c]] = sz;
        U[sz] = c, D[c] = sz;
        if(H[r] < 0) H[r] = L[sz] = R[sz] = sz;
        else R[sz]=R[H[r]], L[R[H[r]]]=sz,L[sz]= H[r],R[H[r]] = sz;
    }
    void del(int c){//精确覆盖,删除涉及C列的集合
        L[R[c]]=L[c],R[L[c]]=R[c];
        FF(i,D,c)FF(j,R,i)U[D[j]]=U[j],D[U[j]]=D[j],--S[col[j]];
    }
    void add(int c){  //精确覆盖,恢复涉及C列的集合
        R[L[c]]=L[R[c]]=c;
        FF(i,U,c)FF(j,L,i)++S[col[U[D[j]]=D[U[j]]=j]];
    }
    bool dance(int k){//精确覆盖
        //(剪枝)if(cnt != -1 && cnt <= d) return 0;//精确匹配输出最小
        if(!R[0]){
            //cnt=min(cnt,k);//精确匹配输出最小
            for(int i = 0;i < k; ++i)
                out[(ans[i]-1)/N]=(ans[i]-1)%N+1; //数独输出
            cnt=k;
            return 1;
        }
        int c=R[0];FF(i,R,0)if(S[c]>S[i])c=i;
        del(c);
        FF(i,D,c){
            FF(j,R,i)del(col[j]);
            ans[k]=row[i];
            if(dance(k+1))return 1;
            //dance(k+1);//精确匹配输出最小
            FF(j,L,i)add(col[j]);
        }
        add(c);
        return 0;
    }
    void remove(int c){//重复覆盖
        FF(i,D,c)L[R[i]]=L[i],R[L[i]]=R[i];
    }
     void resume(int c){//重复覆盖
         FF(i,U,c)L[R[i]]=R[L[i]]=i;
    }
    int A(){//估价函数
        int res=0;
        bool vis[m+1];
        memset(vis,0,sizeof(vis));
        FF(i,R,0)if(!vis[i]){
                res++,vis[i]=1;
                FF(j,D,i)FF(k,R,j)vis[col[k]]=1;
            }
        return res;
    }
    void dance(int now,int &ans){
        if(R[0]==0)ans=max(ans,now); //改为max
        else if(now+A()>ans){
            int temp=INF,c;
            FF(i,R,0)if(temp>S[i])temp=S[i],c=i;
            FF(i,D,c){
                remove(i);
                FF(j,R,i)remove(j);
                dance(now+1,ans);
                FF(j,L,i)resume(j);
                resume(i);
            }
        }
    }
}dlx;


int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    ll num[N];
    int T;
    cin >> T;
    while (T--) {
        cin >> n;
        for (int i = 1; i <= n; ++ i) cin >> num[i];
        dlx.init(n,n);
        for (int i = 1; i <= n; ++ i)
            for (int j = 1; j <= n; ++ j)
                if (num[i] % num[j] == 0 || num[j] % num[i] == 0)
                    dlx.link(i, j);//, cout << i << "  " << j << endl;
        int ans = 0;
        dlx.dance(0, ans);
        cout << ans << endl;
    }

    return 0;
}