之前虽然刷了大概一百道网络流的题目,但是始终是把网络流当作黑盒算法来学。我大概知道了网络流能做什么。
但是对于网络流的代码细节我还是一窍不通。特此写一篇博文来整理,我对网络流的理解。
Ford-Fulkerson算法:
这个算法是一切网络流算法的基础,其最重要的贡献就是增广路定理:找不到增广路的时候,此时的累加流量就是最大流。
所以这个算法最主要的地方就是寻找增广路——每次DFS寻找从S到T路径上流量最小的边。
之后便是残余网络的概念。每次找到增广路之后都修改残余网络。直到不存在增广路的时候,算法结束。
缺陷:因为每次都是dfs所以,太不稳定,会被值域所影响。如下图,图片源自https://www.cnblogs.com/rvalue/p/10650849.html
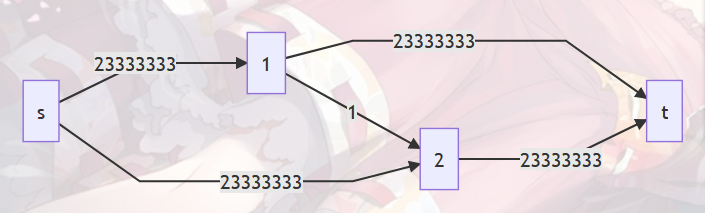
有可能会在1-2之间进行466666666次过程。
Edmonds-Karp算法:
EK算法是上面算法的多项式优化版本。最主要的地方就是用BFS代替了DFS使得每次增广的都是最短路。

图片源自上面链接。
局限:EK算法的劣势就在于, 每次遍历了一遍残量网络之后只能求出一条增广路来增广。
Dnic算法:
相较于EK算法,Dinic的复杂度更为优秀。Dinic最重要的思想就是引入了分层图,让流只能往下一层流。
每次跑DFS都能实现多路增广,增广完之后重新BFS建分层图。一旦建不了分层图那么算法结束。
其中我们说说Dinic代码细节。(BFS就是裸的分层,所以主要是DFS)
inline ll dfs(int u, ll flow) { if(u == T) return flow; ll del = flow; for(int i = cur[u]; ~i; i = edge[i].next){ cur[u] = edge[i].next;//当前弧优化,下次直接从cur[u]开始增广,节省时间 int v = edge[i].to; if (dis[v] == dis[u] + 1 && edge[i].w > 0){//深度+1且残量大于0 ll ans = dfs(v, min(del, edge[i].w));//木桶原理 edge[i].w -= ans;//正向弧减增广流量 edge[i ^ 1].w += ans;//反向弧加增广流量 del -= ans;//总流量减增广流量 if(del == 0) break;//总流量为0则不继续增广 } } return flow - del;//返回本次增广的流量 }
del优化:为什么要设计一个del,通过flow-del来返回增广流量呢?我的理解是,del的意义是可行上界,意思就是有这么多流量流进来。那么我们很容易知道当上界为0的时候肯定就不能增广了,所以直接break。