向量叉积
定义
[vec a imesvec b=|vec a||vec b|sin heta ]
证明
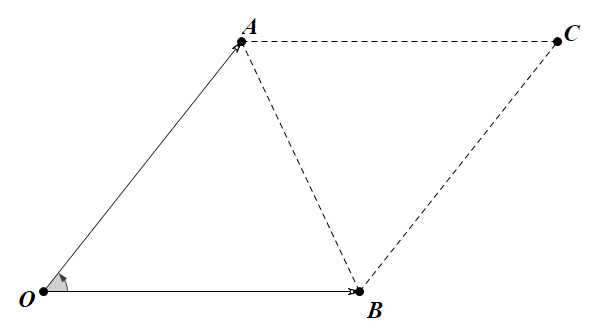
- 证明:在如图所示的平行四边形0ACB中 $$S_{Delta AOC}=frac{1}{2}|vec {a}||vec b|sin heta$$
- 则平行四边形的面积是 $$S=|vec{a}| |vec b|sin heta$$
[vec a cdot vec b=|vec a| |vec b| cos heta
]
[cos heta=frac{vec a cdot vec b}{|vec a| |vec b|}
]
[egin{eqnarray}
sin heta &= & sqrt{1-cos^2 heta} \
&=&frac{sqrt{(|vec a|^2cdot|vec b|)^2-(vec{a}cdot{vec{b})^2}}}{|vec a||vec b|} \
end{eqnarray}
]
[egin{aligned}
S &= sqrt{(|vec a|^2cdot|vec b|)^2-(vec{a}cdot{vec{b})^2}} \
&=sqrt{(x_1^2+y_1^2)(x_2^2+y_2^2)-(x_1x_2+y_1y_2)^2} \
&= sqrt{(x_1y_2)^2+(x_2y_1)^2-2x_1x_2y_1y_2} \
&= sqrt{(x_1y_2-x_2y_1)^2} \
&= |x_1y_2-x_2y_1| \
end{aligned}
]
$overrightarrow {} ( )underleftarrow{ssxxxxxxxxx}( )leftleftarrows{}$