hihoCoder1381

Portal

Description

给出一个(n(nleq10^5))个点的带边权的树。进行(Q)次询问：每次删除树上的(k)条边，求剩下的(k+1)个连通块中最远点对距离的和。(Sigma kleq10^5)，询问之间是独立的。

Solution

神奇而又毒瘤的做法。
考虑如何合并树上两个连通块的答案。设两个连通块的最远点对分别为((v_1,v_2),(v_3,v_4))，那么合并后的最远点对的两个端点一定是({v_1,v_2,v_3,v_4})中的两个。LCA用RMQ求的话时间复杂度是(O(1))。

证明：
设两个连通块通过边((p,q))连通。若合并后的最远路径不经过((p,q))，则其一定是((v_1,v_2),(v_3,v_4))之一。若经过((p,q))，则可以将其看成((u_1,p)+(p,q)+(q,u_2))，而((v_1,p),(v_2,p))必然是以(p)为端点的最长、次长路径，所以(u_1)必然是(v_1,v_2)之一；(u_2)同理。

删除边((u,v))相当于将以(v)为根的子树从原树上断掉，断掉(k)条边相当于将原树变成了以(1)和(v_{1..k})为根的(k+1)个连通块。那么做出原树的DFS序，断掉一个子树就相当于删掉一个区间。如图，子树(1)中的子树(2)和子树(6)被断掉，那么就删掉这两个区间，剩下的({1,3})即以(1)为根的连通块；同理(2)中的(4)被断掉，从(2)的DFS序中删掉(4)的就是({2,5})。

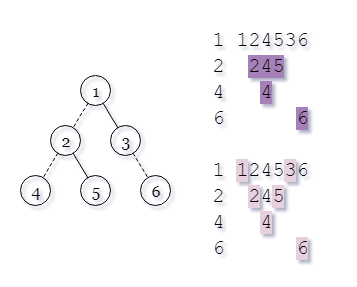
对所有区间排序并递归，可以求出每个连通块中有哪些点，那么该连通块中的最远点对相当于DFS序上的若干个区间的合并。由于新加入一个区间最多把原区间分成三份，所以最多要询问(2k+1)次。用线段树维护DFS序，每个节点记录该区间内的最远点对即可。虽然DFS上连续的点在原树上不一定连通，不过由于我们每次询问的部分都是连通的所以没关系啦。

时间复杂度(O(lognSigma k))。

Code

//Little Y's Tree
#include <algorithm>
#include <cstdio>
using std::sort; using std::max; using std::swap;
typedef long long lint;
inline char gc()
{
    static char now[1<<16],*s,*t;
    if(s==t) {t=(s=now)+fread(now,1,1<<16,stdin); if(s==t) return EOF;}
    return *s++;
}
inline int read()
{
    int x=0; char ch=gc();
    while(ch<'0'||'9'<ch) ch=gc();
    while('0'<=ch&&ch<='9') x=x*10+ch-'0',ch=gc();
    return x;
}
const int N=1e5+10;
int n;
int cnt,h[N];
struct edge{int u,v,w,nxt;} ed[N<<1];
void edAdd(int u,int v,int w)
{
    cnt++; ed[cnt].u=u,ed[cnt].v=v,ed[cnt].w=w,ed[cnt].nxt=h[u],h[u]=cnt;
    cnt++; ed[cnt].u=v,ed[cnt].v=u,ed[cnt].w=w,ed[cnt].nxt=h[v],h[v]=cnt;
}
int fa[N],dpt[N]; lint dst[N];
int dfCnt1,dfn1[N],fr1[N],to1[N];
int dfCnt2,dfn2[N<<1],fr2[N];
void dfs(int u)
{
    dfn1[++dfCnt1]=u; fr1[u]=dfCnt1;
    dfn2[++dfCnt2]=u; fr2[u]=dfCnt2;
    for(int i=h[u];i;i=ed[i].nxt)
    {
        int v=ed[i].v,w=ed[i].w;
        if(v==fa[u]) continue;
        fa[v]=u,dpt[v]=dpt[u]+1,dst[v]=dst[u]+w;
        dfs(v); dfn2[++dfCnt2]=u;
    }
    to1[u]=dfCnt1;
}
int Lg2[N<<1],rmq[N<<1][20];
void bldLCA()
{
    Lg2[1]=0;
    for(int i=2;i<=dfCnt2;i++) Lg2[i]=Lg2[i>>1]+1;
    for(int i=1;i<=dfCnt2;i++) rmq[i][0]=dfn2[i];
    for(int k=1;k<=18;k++)
        for(int i=1;i+(1<<k-1)<=dfCnt2;i++)
        {
            int r1=rmq[i][k-1],r2=rmq[i+(1<<k-1)][k-1];
            rmq[i][k]=dpt[r1]<dpt[r2]?r1:r2;
        }
}
int lca(int u,int v)
{
    int i=fr2[u],j=fr2[v];
    if(i>j) swap(i,j);
    int t=Lg2[j-i+1];
    int r1=rmq[i][t],r2=rmq[j-(1<<t)+1][t];
    return dpt[r1]<dpt[r2]?r1:r2;
}
lint dist(int u,int v) {return dst[u]+dst[v]-2*dst[lca(u,v)];}
#define Ls (p<<1)
#define Rs (p<<1|1)
int rt=1; int maxP=0;
struct node
{
    lint len; int v1,v2;
    node(lint _len=0,int _v1=0,int _v2=0) {len=_len,v1=_v1,v2=_v2;}
}nd[N<<2];
node operator +(node x,node y)
{
    if(x.v1==0) return y; else if(y.v1==0) return x;
    node z=node(0,0,0);
    lint d[10],d0=0;
    d[1]=dist(x.v1,x.v2),d[2]=dist(x.v1,y.v1),d[3]=dist(x.v1,y.v2);
    d[4]=dist(x.v2,y.v1),d[5]=dist(x.v2,y.v2),d[6]=dist(y.v1,y.v2);
    for(int i=1;i<=6;i++) d0=max(d0,d[i]);
    if(d[1]==d0) z=node(d[1],x.v1,x.v2);
    else if(d[2]==d0) z=node(d[2],x.v1,y.v1);
    else if(d[3]==d0) z=node(d[3],x.v1,y.v2);
    else if(d[4]==d0) z=node(d[4],x.v2,y.v1);
    else if(d[5]==d0) z=node(d[5],x.v2,y.v2);
    else if(d[6]==d0) z=node(d[6],y.v1,y.v2);
    return z;
}
void update(int p) {nd[p]=nd[Ls]+nd[Rs];}
void bldTr(int p,int L0,int R0)
{
    maxP=max(maxP,p);
    if(L0==R0) {nd[p]=node(0,dfn1[L0],dfn1[L0]); return;}
    int mid=L0+R0>>1;
    bldTr(Ls,L0,mid),bldTr(Rs,mid+1,R0);
    update(p);
}
int optL,optR;
node query(int p,int L0,int R0)
{
    if(optL<=L0&&R0<=optR) return nd[p];
    int mid=L0+R0>>1; node res=node(0,0,0);
    if(optL<=mid) res=res+query(Ls,L0,mid);
    if(mid<optR) res=res+query(Rs,mid+1,R0);
    return res;
}
struct qRec{int fr,to; node ans;} q[N];
bool cmpQ(qRec x,qRec y) {return x.fr<y.fr;}
int m,now;
//solve(x)解决区间x及其内部区间，并将now移动到x外的第一个
void solve(int x)    
{
    if(x>m) return;
    now++; int pre=q[x].fr;
    while(now<=m&&q[now].to<=q[x].to)
    {
        optL=pre,optR=q[now].fr-1;
        if(optL<=optR) q[x].ans=q[x].ans+query(rt,1,n);
        pre=q[now].to+1;
        solve(now);
    }
    optL=pre,optR=q[x].to;
    if(optL<=optR) q[x].ans=q[x].ans+query(rt,1,n);
}
int main()
{
    n=read();
    for(int i=1;i<=n-1;i++)
    {
        int u=read(),v=read(),w=read();
        edAdd(u,v,w);
    }
    fa[1]=0,dfs(1);
    bldLCA(); bldTr(rt,1,n);
    int Q=read();
    while(Q--)
    {
        m=read();
        for(int i=1;i<=m;i++)
        {
            int x=read()<<1; int u=ed[x].u,v=ed[x].v;
            if(dpt[u]>dpt[v]) swap(u,v);
            q[i].fr=fr1[v],q[i].to=to1[v];
            q[i].ans=node(0,0,0);
        }
        m++; q[m].fr=1,q[m].to=n,q[m].ans=node(0,0,0);
        sort(q+1,q+m+1,cmpQ);
        solve(now=1);
        lint res=0;
        for(int i=1;i<=m;i++) res+=(q[i].ans).len;
        printf("%lld
",res);
    } 
    return 0;
}

P.S.

Icefox不到100行orz，我写了150+