上一篇,我们学习了二叉树的一些属性,定义,种类等。今天,我们主要学习它的存储结构、基本操作、与经典算法。二叉树之所以在数据结构中那么重要,正是因为它的存储结构、它的严谨规范。同时,也衍生了很多关于二叉树的经典算法,例如下面我们要学习的赫夫曼编码。不论,我们将来是做程序员、还是DBA。数据结构,是最最基本、最最重要的知识。我们把数据结构、计算机体系、计算机操作系统、网络安全等方面的知识掌握了,学习最新的编程语言、成熟框架等等,就如同砍瓜切菜般轻松。所以,我们一定要懂得磨刀不误砍柴功的道理。不要急于学习最新的编程语言,最新的框架,掌握基本知识才是王道。好了,闲话不多说了,开始吧。
1.二叉链表:
在学习树的存储结构时,我们知道单单使用顺序存储结构,不能很好的表现出树结点之间的逻辑关系。但是,二叉树有严格的规范,可以使用顺序存储结构。
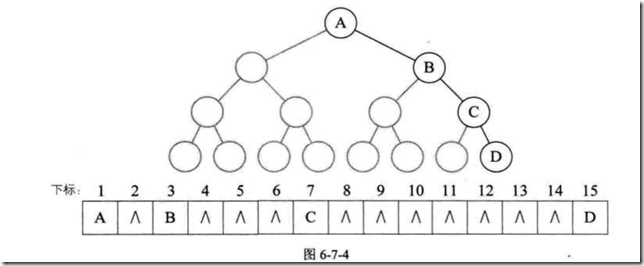
上图是个完全二叉树,我们采用顺序存储的方式存储它。使用一维数组存放结点:
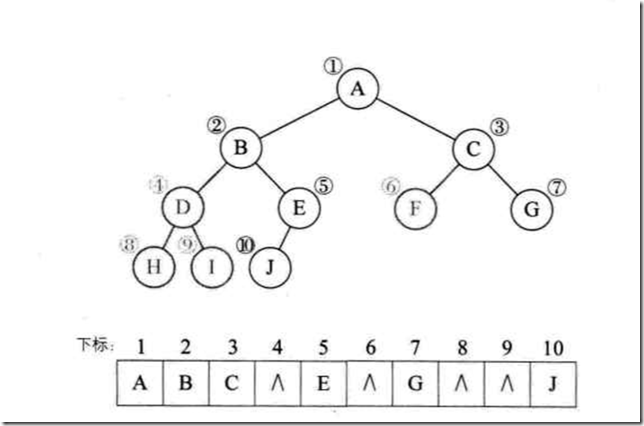
如果,不是一颗完全二叉树,我们可以把缺少的结点使用^表示出来,如下图:
浅色数字是不存在的结点,我们使用^表示。所以使用顺序存储是可以表示二叉树的结点之间逻辑。
但是问题又来了,一颗深度为k的右斜树,结点有k个,但是需要开辟2^k-1个空间。这是一个极大的浪费,是不可取的。
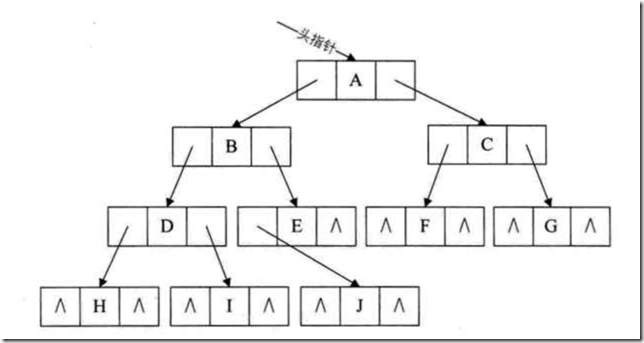
所以,二叉链表就出场了。因为二叉树,最多只有两棵子树,所以我们可以这样设计结点结构:
data为数据域,lchild、rchild分别指向左子树的根结点、右子树的根结点。
//二叉树的二叉链表结点结构定义 typedef struct BiTNode /*结点结构*/ { TElemType data; /*结点数据*/ BiTNode *lchild、*rchild;/*左右孩子指针*/ }BiTNode,*BiTree;
这是二叉树的二叉链表结点结构定义和结构示意图。
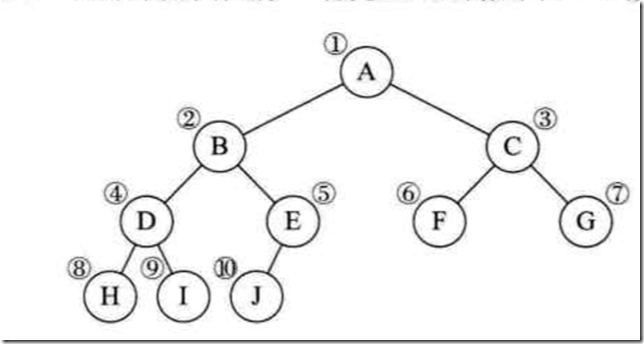
2.遍历二叉树(Traversing Binary Tree):
二叉树的遍历(traversing binary tree):从根结点开始,以某种次序遍历各个结点,确保每个结点都访问过并且仅访问过一次。
为什么要研究二叉树的遍历呢?我们通过图来展示二叉树的结构,非常直观易于理解。但是计算机,只有循环、判断等操作,计算机只能处理线性序列。二叉树的遍历,某种意义上就是将结点转变为线性序列。如果我们限制了从左向右遍历,那么有以下四种遍历方式:
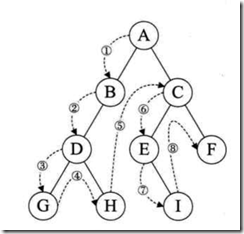
a.前序遍历:
从根结点开始,先遍历左子树,在遍历右子树。
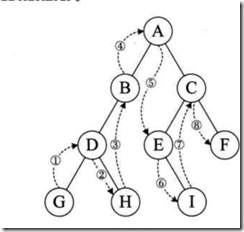
b.中序遍历:
从根结点开始,先中序编列左子树,在遍历根结点,最后遍历右子树。note:从根结点开始,不是意味着先遍历根结点。
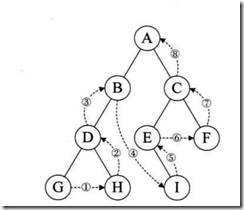
c.后序遍历:
从左到右,先叶子结点,再根结点。
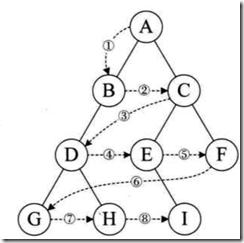
D.层次遍历:
从根结点开始,从上而下,同一层中从左到右的顺序遍历。
下面我看一下各中遍历方法的实现代码:
/*二叉树的前序遍历递归算法*/ void PreOrderTraverse(BiTree T) { if(T==Null) //如果是空树,则返回 return; printf("%C",T-data);//打印数据,可以换成任何操作 PreOrderTraverse(T->lchild); //前序访问左子树 PreOrderTraverse(T->rchild);//前序访问右子树 }
/*二叉树的中序递归算法*/ void InOrderTraverse(BiTree T) { if(T==Null) //判断树是否为空 return; InOrderTraverse(T->lchild);//中序遍历左子树 Printf("%c",T->data); //打印数据,可以换成任何操作 InOrderTraverse(T->rchild);//中序遍历右子树 }
/*二叉树的后序递归算法*/ void PostOrderTraverse(BiTree T) { if(T==Null) //判断树是否为空 return ; PostOrderTraverse(T->lchild);//后序遍历左子树 PostOrderTraverse(T->rchild);//后序遍历右子树 Printf("%C",T->data);//打印数据,可以换成任何操作 }
以上就是二叉树不同遍历次序的实现算法,这些算法我们用到了递归。递归算法可以使我们的算法更加飘逸,简洁。