定义:
离散化,把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率。
理解:
简单粗暴的举个栗子。通过数轴比较1和100000000大小,那么想都不用想100000000肯定比1大。如果必须通过数轴比较呢?没有人会画一个长为大于100000000的数轴找到一个准确的点去比较。只会画出两个点来表示相对大小。这就是离散化的意义,如果每个数据元素的具体值并不重要,重要的是他们之间的大小关系,那么我们就可以进行离散化。
栗子:
有N=6个数,分别为5,6,-1,-2,8,-2,统计负数的个数。我们可以用数组下标表示数值,数组的值表示次数,如果采取这种方法,我们只能统计正数出现的次数,如何统计负数的出现次数呢,那么先离散化再统计。
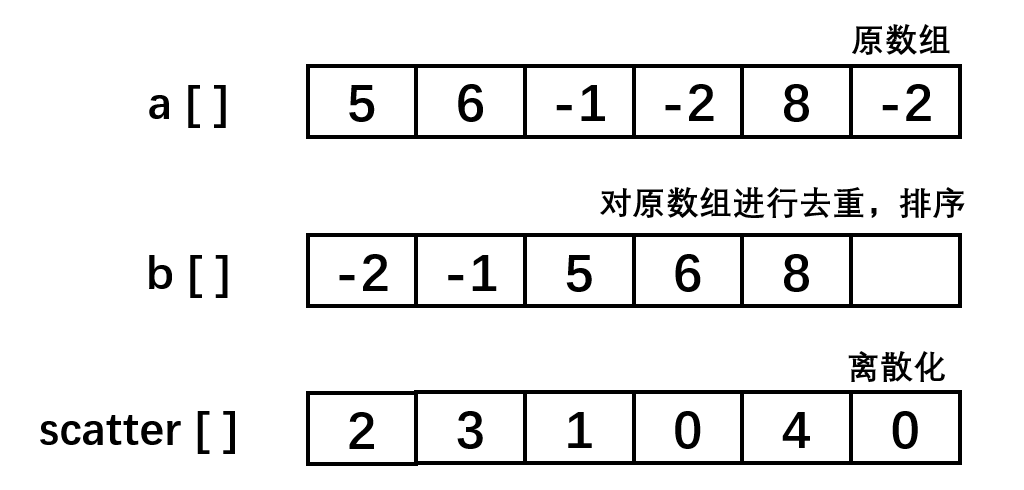
scatter[]即为a[]离散化后的结果。scatter[]忽略了a[]的具体数值,保留了其相对大小。 因为a[i]=b[scatter[i]],scatter[i]>=0,b[]中数值唯一,scatter[]中数值出现的次数为b[scatter[i]]出现的次数,即a[i]出现次数。
板子:
#include<bits/stdc++.h>
using namespace std;
const int maxn=100005;
int a[maxn],b[maxn],scatter[maxn];
int main()
{
int i,n,nn;
scanf("%d",&n);
for(i=0;i<n;i++)
{
scanf("%d",&a[i]);
b[i]=a[i];
}
sort(b,b+n);
nn=unique(b,b+n)-b;
for(i=0;i<n;i++) scatter[i]=lower_bound(b,b+nn,a[i])-b;
system("pause");
return 0;
}