马拉车(Manachar)——最长回文串

定义：

  Manachar算法主要是处理字符串中关于回文串的问题的，它可以在 O（n） 的时间处理出以字符串中每一个字符为中心的回文串半径，由于将原字符串处理成两倍长度的新串，在每两个字符之间加入一个特定的特殊字符，因此原本长度为偶数的回文串就成了以中间特殊字符为中心的奇数长度的回文串了。 Manacher算法提供了一种巧妙的办法，将长度为奇数的回文串和长度为偶数的回文串一起考虑，具体做法是，在原字符串的每个相邻两个字符中间插入一个分隔符，同时在首尾也要添加一个分隔符，分隔符的要求是不在原串中出现，一般情况下可以用#号。(引)

实现：

  预处理：

   在原字符串的每一个字符的左右都加上一个特殊字符，比如加上 '#'，然后在开头加上与'#'不同的字符，比如’$’。（这样做的目的是为了不论原字符串是奇数还是偶数个，处理之后得到的字符串的个数都是奇数个，这样就不用分情况讨论了，可以一起搞定。）

 

 

 

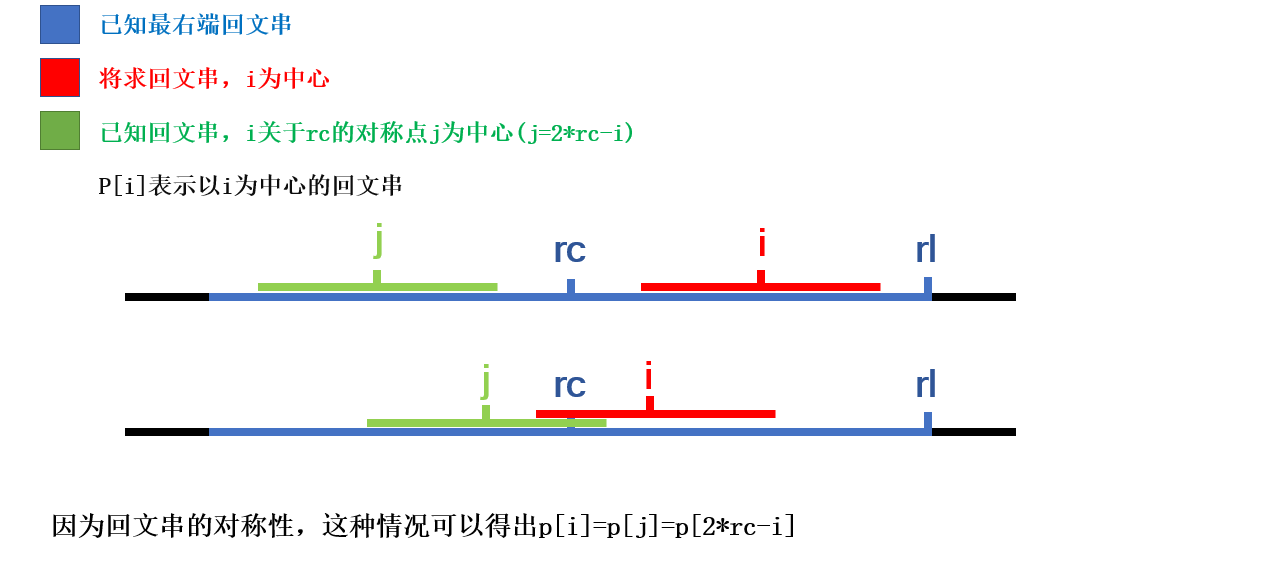
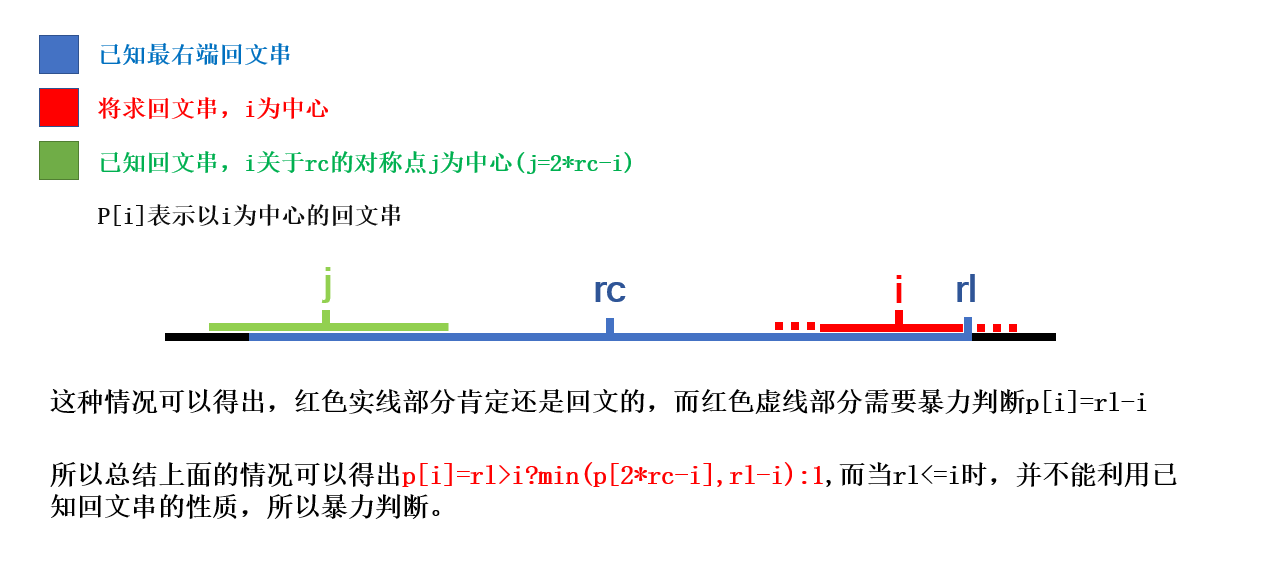
  马拉车的主要思想就是利用回文串两边相同的性质，用已知回文串去推未知回文串。

参考Grandyang

代码

int p[maxn];
void Manacher(string s) 
{
    string t="$#";
    for (int i=0;i<s.size();++i) //预处理
    {
      t+=s[i];
      t+="#";
    }
    //rc，rl为能延伸到最右边的回文串的中心和右端点
    //ansCenter,ansLen为最长回文串的中心和半径
    int rl=0,rc=0,ansLen=0,ansCenter=0; 
    for(int i=1;i<t.size();++i) 
    {
      p[i]=rl>i?min(p[2*rc-i],rl-i):1;
      while(t[i+p[i]]==t[i-p[i]]) ++p[i]; //暴力更新
      if(rl<i+p[i]) //更新
      {
        rl=i+p[i];
        rc=i;
      }
      if(ansLen<p[i]) //更新
      {
        ansLen=p[i];
        ansCenter=i;
      }
    }
    //最长回文串
    cout<<s.substr((ansCenter-ansLen)/2,ansLen-1)<<endl; 
    return ;
}