两个等长升序序列找中位数

题目

　　 一个长度为 L 的升序序列 S，处在第个位置的数称为 S 的中位数。例如，若序列 ，则  的中位数是 15，两个序列的中位数是含他们所有元素的升序序列的中位数。例如，若 ，则  和  的中位数是 11。现在有两个等长升序序列 A 和 B，试设计一个算法，找出两个序列 A 和 B 的中位数。

分析

暴力

　　把 A 和 B 混合到一起再找中位数。实现方法简单且不为本篇文章讨论重点，不再详细叙述。

减治

　　将升序序列左右两边同时减去相等个数的数字，中位数不变。

　　令两个升序序列 A , B 的中位数为 a , b，求解过程如下：

　　　　① 若 a = b，则 a 或 b 即为所求中位数。

　　　　② 若 a < b，则舍弃序列 A 中较小的一半，同时舍弃序列 B 中较大的一半，要求两次舍弃的长度相等。

　　　　③ 若 a > b，则舍弃序列 A 中较大的一半，同时舍弃序列 B 中较小的一半，要求两次舍弃的长度相等。

　　在保留的两个升序序列中，重复过程 ① ，② ，③，直到两个序列中均只含一个元素时为止，较小者即为所求的中位数。 

① a = b

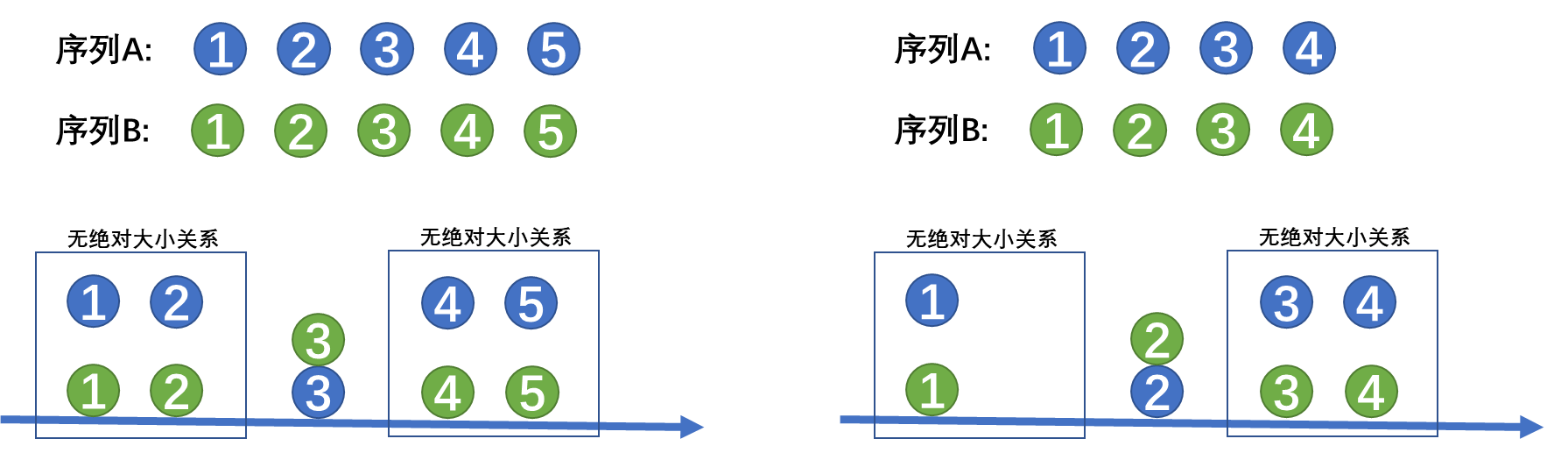
　　a = b时，容易得到两个序列在数轴上的大小关系，虽然左右两边并没有绝对大小关系，但是中位数的选取只跟中间位置有关，所以并不影响。

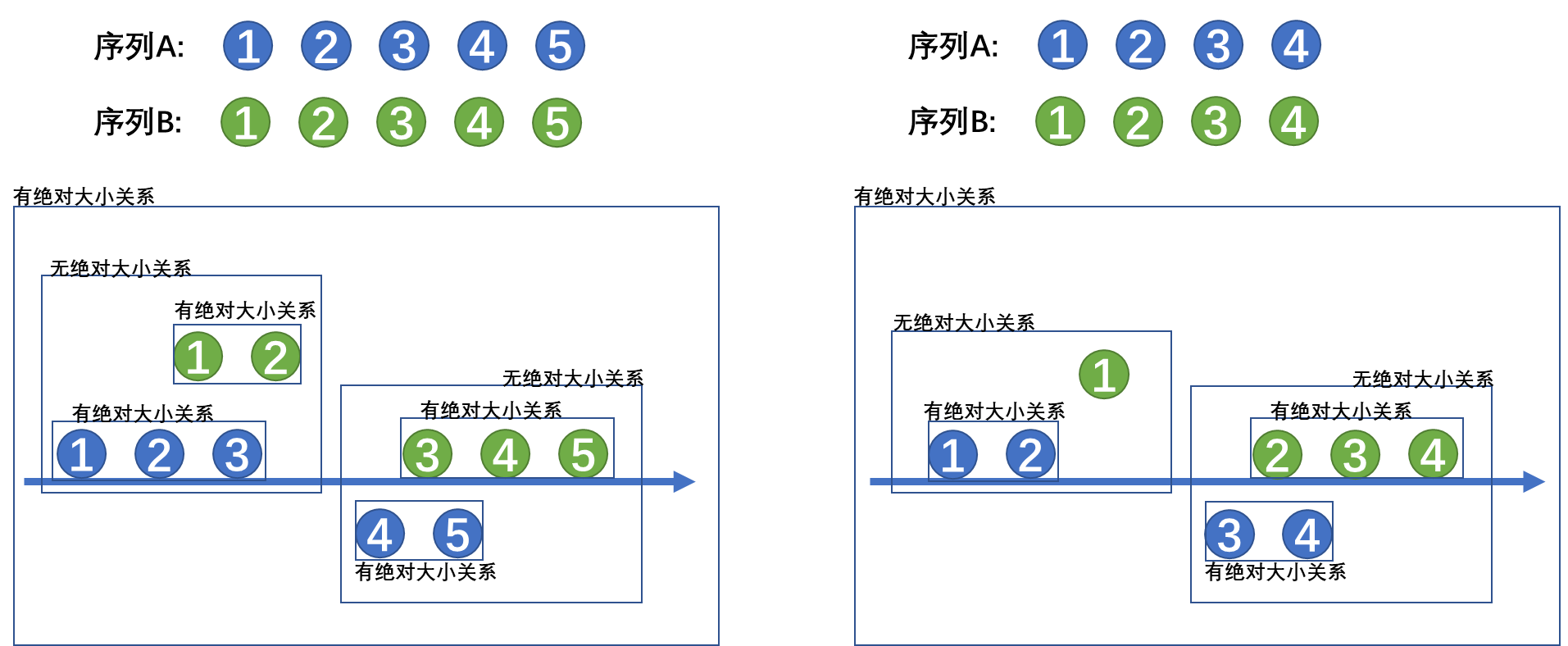
② a != b

　　a != b时，以 a < b 为例。

　　对于奇数个数序列：

　　　　因为中位数只与升序序列的位置有关，通过左图中的有/无绝对大小关系可得 蓝1，蓝2，绿4，绿5 代表的四个数绝对不可能在中间位置（5），所以把他们删去，即中位数的大小范围为 [a , b] 。

　　对于偶数个数序列：

　　　　还是那句话因为中位数只与升序序列的位置有关，通过右图中的有/无绝对大小关系可得 蓝1，蓝2，绿3，绿4 代表的四个数绝对不可能在中间位置（4），所以把他们删去，即中位数的大小范围为 ( a , b ]。

 

实现

int M_Search(int A[], int B[], int n) 
{
    int s1=0,d1=n-1,m1,s2=0,d2=n-2,m2;//A，B序列的首位数、中位数、末位数
    while (s1 != d1 || s2 != d2) 
    {
        m1=(s1+d1)/2;
        m2=(s2+d2)/2;
        if (A[m1]==B[m2])             //当两个中位数相等，即为所求中位数
            return A[m1];
        else if (A[m1]<B[m2]) 
        {
            if((s1+d1)%2==0)          //当元素个数为奇数
            { 
                s1=m1;                //舍弃A中间点以前的部分且保留中间点
                d2=m2;                //舍弃B中间点以后的部分且保留中间点
            }
            else                      //当元素个数为偶数
            {                      
                s1=m1+1;              //舍弃A中间点及中间点以前的部分
                d2=m2;                //舍弃B中间点以后的部分且保留中间点
            }
            
        }
        else                          //同理
        {
            if ((s2+d2)%2==0) 
            {
                d1=m1;
                s2=m2;
            }
            else 
            {
                d1=m1;
                s2=m2+1;
            }
        }

    }
    return A[s1]<B[s2]?A[s1]:B[s2];
}