1 变换矩阵
平移矩阵
[egin{bmatrix}
1 & 0 & t_x\
0 & 1 & t_y\
0 & 0 & 1\
end{bmatrix}
egin{bmatrix}
x \
y \
1 \
end{bmatrix}
=
egin{bmatrix}
x +t_x\
y +t_y\
1 \
end{bmatrix}
]
缩放矩阵
[egin{bmatrix}
s_x & 0 & 1\
0 & s_y & 1\
0 & 0 & 1\
end{bmatrix}
egin{bmatrix}
x \
y \
1 \
end{bmatrix}
=
egin{bmatrix}
s_xx \
s_yy \
1 \
end{bmatrix}
]
旋转矩阵
[egin{bmatrix}
cos heta & -sin heta & 0\
sin heta & cos heta & 0\
0 & 0 & 1\
end{bmatrix}
egin{bmatrix}
x \
y \
1 \
end{bmatrix}
=
egin{bmatrix}
xcos heta -ysin heta\
xsin heta +ycos heta\
1 \
end{bmatrix}
]
平移和缩放都很好理解,旋转矩阵可能要稍微推到一下,这里用到两角和差公式,如下:
[sin(alphapm heta) = sinalpha cos heta pm cosalpha sin heta \
cos(alphapm heta) = cosalpha cos heta mp sinalpha sin heta
]
P是旋转变换前的点,P'是旋转变换后的点,P与坐标轴的夹角为(alpha),P'与P的夹角为( heta),已知P的坐标和旋转的角度( heta)
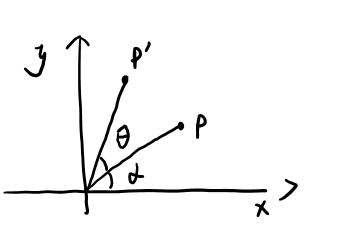
因为旋转前后P和原点的距离没有变化,所以设为( ho),则有
[
hocos(alpha+ heta) = x^{'}\
hosin(alpha+ heta) = y^{'}\
hocosalpha = x\
hosinalpha = y\
]
利用两角和公式,即可得到
[xcos heta -ysin heta = x^{'}\
xsin heta +ycos heta = y^{'}\
]
上述的缩放也好,旋转也好都是相对于原点的,如果想相对于某个点进行缩放或者旋转,可以先把参考点平移至远点,然后再进行缩放或者旋转,完毕后,再平移回去。例如在坐标系中有一个矩形,我们想相对于它的中心进行缩放,和旋转,那么将其中心点平移至远点,然后进行缩放,然后再平移回去。
(M_{composition} = A_{moveBack}A_{rotate}A_{scale}A_{moveToOrigin}P_{rect})
2 在WebGL中如何操作
在vertex shader中,对传入的顶点数据进行变换(乘变换矩阵),并赋给gl_Position
attribute vec2 a_position;
uniform mat3 u_matrix;//预先在js中计算出变换矩阵,然后传入shader中
void main() {
// 使位置和矩阵相乘
gl_Position = vec4((u_matrix * vec3(a_position, 1)).xy, 0, 1);
}
例如2D的投影矩阵,将像素空间转换为裁剪空间。像素空间默认的是原点在左上角,y轴朝下,坐标范围为[0,width],[0,height],而裁剪空间的原点在中心,y轴朝上,范围为[-1,1]。把在像素空间中定义的点,转换到裁剪空间中。
- 将像素坐标缩放到[0,1]
- 缩放到[0,2]
- 坐标-1,变换为[-1,1]
- 将y轴翻转
用变换矩阵来表示,就是
[M_{projection}=
egin{bmatrix}
1 & 0 & 0\
0 & -1 & 0\
0 & 0 & 1\
end{bmatrix}
egin{bmatrix}
1 & 0 & -1\
0 & 1 & -1\
0 & 0 & 1\
end{bmatrix}
egin{bmatrix}
2 & 0 & 0\
0 & 2 & 0\
0 & 0 & 1\
end{bmatrix}
egin{bmatrix}
frac{1}{width} & 0 & 0\
0 & frac{1}{height} & 0\
0 & 0 & 1\
end{bmatrix}
=
egin{bmatrix}
frac{2}{width} & 0 & -1\
0 & frac{-2}{height} & 1\
0 & 0 & 1\
end{bmatrix}
]
所以在做变换的时候,可以基于像素坐标进行变换,最后再乘上投影矩阵,将像素空间变换到裁剪空间