数据结构 堆排序

　　堆排序是一种树形选择排序方法。在排序过程中，将L[1...n]看成是一棵完全二叉树的顺序存储结构，通过完全二叉树的双亲结点（parent）和孩子结点之间的内在关系，在当前无序区中选择最大（或最小）的元素。

　　堆的定义：n个关键字序列L[1...n]称为堆，当且仅当该序列满足：

　　1 L[i]<=L[2i]且L[i]<=L[2i+1]

　　2 L[i]>=L[2i]且L[i]>=L[2i+1]

　　（1<=i<=|_n/2_|，后者表示小于或等于n/2的最大整数）

　　满足第一种情况的堆称为小顶堆，满足第二种情况的堆称为大顶堆。在小顶堆中，对于任意结点，它是作为根结点的子树中最小元素，根结点是最小元素。大顶堆与此相反，根结点是最大元素。

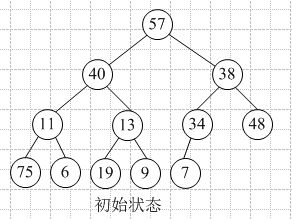
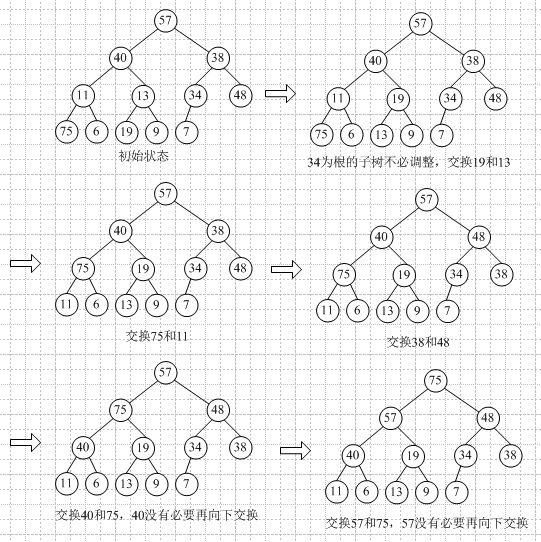
　　构造初始堆：n个结点的完全二叉树，最后一个结点是第|_n/2_|个结点的孩子结点。对某个结点为根的子树进行筛选（对于大顶堆，如果根结点值小于孩子结点较大者，则交换），如果破坏了下一级的堆，则向后筛选，直到以该结点为根的子树构成堆。向前依次对各结点（|_n/2_|~1）重复上述过程。

　　举例（自下向上逐步调整为大顶堆）：

　　

　　

　　

　　Java代码：

// 构造初始大顶堆
private void buildMaxHeap(int[] arr, int length) {
    // 反复调整堆
    for (int i = length / 2; i >= 1; i--) {
        adjustDown(arr, i, length);
    }
} 

　　

// 向下调整堆
private void adjustDown(int[] arr, int parent, int length) {
    // 暂存双亲结点值
    int temp = arr[parent]; 

    // 沿着较大的孩子结点向下筛选
    for (int child = parent << 1; child <= length; child <<= 1) {
        // 如果存在右孩子结点，并且右孩子结点的值大于左孩子结点，则选取右孩子结点的下标
        if (child + 1 <= length && arr[child + 1] > arr[child]) {
            child++;
        }

        // 如果双亲结点值大于孩子结点，则结束筛选
        if (temp >= arr[child]) {
            break;
        }

        // 把孩子结点的值赋给双亲结点
        arr[parent] = arr[child];
        // 把孩子结点的下标赋给双亲结点
        parent = child;
    }
    
    // 把双亲结点值放在最终位置上
    arr[parent] = temp;
}

 

　　排序堆：交换堆顶元素和堆底元素（堆的最后一个元素），原来的堆顶元素不再属于堆，从根结点开始向下调整，把剩余的元素重新建成堆。重复上述过程，直到堆中只剩一个元素。

　　举例：

　　

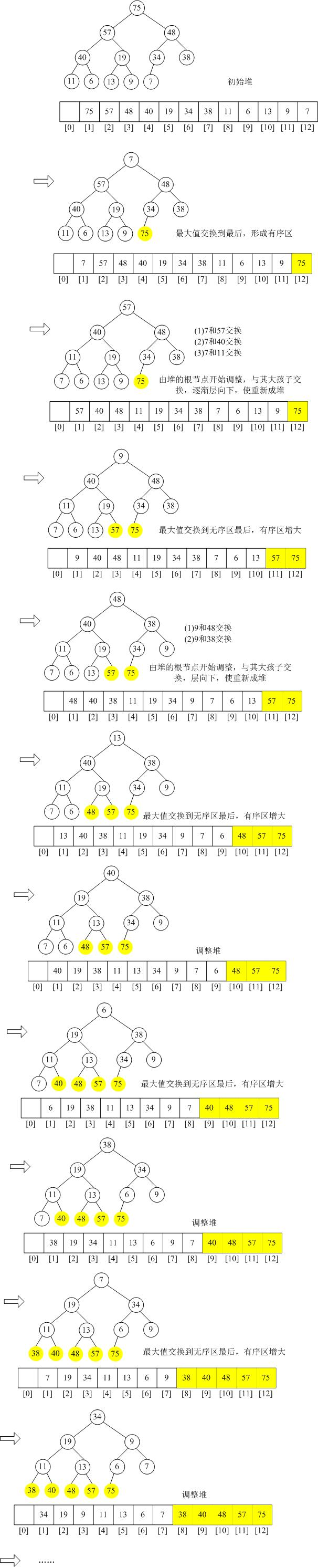
　　Java代码：

// 堆排序
public void heapSort(int[] arr, int length) {
    // 构造初始大顶堆
    buildMaxHeap(arr, length);
    
    // length-1次趟排序堆
    for (int i = length; i > 1; i--) {
        // 交换堆顶元素和堆底元素
        int temp = arr[i];
        arr[i] = arr[1];
        arr[1] = temp;

        // 把剩余的i-1个元素调整成大顶堆
        adjustDown(arr, 1, i - 1);
        System.out.format("第%d趟: ", length - i);
        print(arr, 1, length);
    }
}

　　完整的Java代码：

public class HeapSort {
    // 构造初始大顶堆
    private void buildMaxHeap(int[] arr, int length) {
        // 反复调整堆
        for (int i = length / 2; i >= 1; i--) {
            adjustDown(arr, i, length);
        }
    }
    
    // 向下调整堆
    private void adjustDown(int[] arr, int parent, int length) {
        // 暂存双亲结点值
        int temp = arr[parent]; 

        // 沿着较大的孩子结点向下筛选
        for (int child = parent << 1; child <= length; child <<= 1) {
            // 如果存在右孩子结点，并且右孩子结点的值大于左孩子结点，则选取右孩子结点的下标
            if (child + 1 <= length && arr[child + 1] > arr[child]) {
                child++;
            }

            // 如果双亲结点值大于孩子结点，则结束筛选
            if (temp >= arr[child]) {
                break;
            }

            // 把孩子结点的值赋给双亲结点
            arr[parent] = arr[child];
            // 把孩子结点的下标赋给双亲结点
            parent = child;
        }
        
        // 把双亲结点值放在最终位置上
        arr[parent] = temp;
    }
    
    // 堆排序
    public void heapSort(int[] arr, int length) {
        // 构造初始大顶堆
        buildMaxHeap(arr, length);
        
        // length-1次趟排序堆
        for (int i = length; i > 1; i--) {
            // 交换堆顶元素和堆底元素
            int temp = arr[i];
            arr[i] = arr[1];
            arr[1] = temp;

            // 把剩余的i-1个元素调整成大顶堆
            adjustDown(arr, 1, i - 1);
            System.out.format("第%d趟: ", length - i);
            print(arr, 1, length);
        }
    }

    // 打印
    public void print(int[] arr, int begin, int end) {
        for (int i = begin; i <= end; i++) {
            System.out.print(arr[i] + " ");
        }
        
        System.out.println();
    }

    public static void main(String[] args) {
        // 待排序数组
        int[] arr = {0, 57, 40, 38, 11, 13, 34, 48, 75, 6, 19, 9, 7};

        // 调用快速排序方法
        HeapSort heap = new HeapSort();
        System.out.print("排序前: ");
        int length = 12;
        heap.print(arr, 1, length);
        heap.heapSort(arr, length);
        System.out.print("排序后: ");
        heap.print(arr, 1, length);
    }
}

　　输出结果：

排序前: 57 40 38 11 13 34 48 75 6 19 9 7 
第0趟: 57 40 48 11 19 34 38 7 6 13 9 75 
第1趟: 48 40 38 11 19 34 9 7 6 13 57 75 
第2趟: 40 19 38 11 13 34 9 7 6 48 57 75 
第3趟: 38 19 34 11 13 6 9 7 40 48 57 75 
第4趟: 34 19 9 11 13 6 7 38 40 48 57 75 
第5趟: 19 13 9 11 7 6 34 38 40 48 57 75 
第6趟: 13 11 9 6 7 19 34 38 40 48 57 75 
第7趟: 11 7 9 6 13 19 34 38 40 48 57 75 
第8趟: 9 7 6 11 13 19 34 38 40 48 57 75 
第9趟: 7 6 9 11 13 19 34 38 40 48 57 75 
第10趟: 6 7 9 11 13 19 34 38 40 48 57 75 
排序后: 6 7 9 11 13 19 34 38 40 48 57 75 

 

　　堆排序性能分析：

　　空间复杂度：仅使用了常数个辅助单元，所以空间复杂度是O(1)。

　　时间复杂度：建堆时间复杂度是O(n)，之后执行n-1次向下调整操作，每次调整的时间复杂度是O(h)，所以在最好、最坏和平均情况下，堆排序的时间复杂度是O(nlog₂n)。

　　稳定性：筛选后可能把后面的相同元素调整到前面，所以堆排序不稳定。例如，表L={1，2，2}，构造初始堆后L={2，1，2}，最终排序结果是L={1，2，2}，相同元素的相对次序发生了变化。

 

　　参考资料

　　《2017年数据结构联考复习指导》P296-298

　　数据结构示例——堆排序过程