leetcode 48 矩阵旋转可以这么简单

一行代码解决矩阵旋转（方法三）。

方法1：

坐标法

def rotate(self, matrix):
    n = len(matrix)  # 求出矩阵长度
    m = (n + 1) // 2  # 求出层数
    for k in range(m):
        t = n - 2 * k - 1  # 需旋转的次数
        for i in range(t):
            #                                        不考虑 i                                考虑 i
            # d1（左上），行与k成正比，列与k成正比且与i成正比 [k][k]  ---------------》 [k][k + i]
            # d2（左下），行与k成反比且与i成反比，列与k成正比 [n - 1 - k][k]            [n - 1 - k - i][k]
            # d3（右下），行与k成反比，列与k成反比且与i成反比 [n - 1 - k][n - 1 - k]    [n - 1 - k][n - 1 - k - i]
            # d4（右上），行与k成正比且与i成正比，列与k成反比 [k][n - 1 - k]            [k + i][n - 1 - k]
            temp = matrix[k][k + i]                  #k代表层
            matrix[k][k + i] = matrix[n - 1 - k - i][k]    # k层  左上角  行不变  左下角 列不变
            matrix[n - 1 - k - i][k] = matrix[n - 1 - k][n - 1 - k - i]
            matrix[n - 1 - k][n - 1 - k - i] = matrix[k + i][n - 1 - k]
            matrix[k + i][n - 1 - k] = temp

解释代码：

这里的坐标是不是很晕，这个是如何对应起来的呢？

1、首先我们把矩阵的每一圈看做一次操作（底下的红色圈代表一次调整）

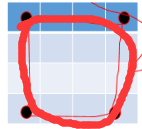对于宽度为n的我们需要 n/2次调整就可以结束。  这个次数为外层循环 K

2、对于每一次调整我们需要进行多次操作，因为每一次我们调整四个点（图中黑点）

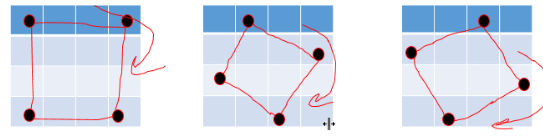每次往内缩缩小了2个格子  每一次内部调整次数为 n-2*k -1

 3、现在外部循环为1 中次数  内部为 2中次数，那么坐标关系怎么处理呢？

                       只考虑1                                           考虑2

d1（左上）[k][k]                    [k][k+i]
d2（左下）[n - 1 - k][k]            [n - 1 - k - i][k]
d3（右下）[n - 1 - k][n - 1 - k]    [n - 1 - k][n - 1 - k - i]
d4（右上）[k][n - 1 - k]            [k + i][n - 1 - k]

第一步：我们先不考虑2 只考虑1中坐标变化关系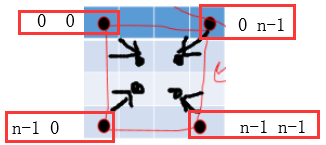 每一个点都是往内部走k为层数（对照上述的关系看） 

当k变化时 d1（左上）坐标[0+k][0+k]   与k均成正比    d2（左下）坐标[n - 1 - k][k] 横坐标反比 纵坐标正比   以此类推。。。。。。

第二步：现在考虑1 

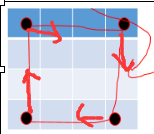
左上角坐标内部调整时，下一个为它右侧，纵坐标 ++   

左下角坐标内部调整时，下一个为它上侧，横坐标  --  

右下角坐标内部调整时，下一个为它左侧，纵坐标  -- 

右上角坐标内部调整时，下一个为它下侧，横坐标 ++   

方法2（先对矩阵转置，然后进行水平翻转）：

class Solution1:  #转置和水平翻转两个步骤。
    def rotate(self, matrix) -> None:
        for i in range(len(matrix)):
            for j in range(i, len(matrix[0])):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

        for row in matrix:
            row.reverse()

方法3（一行代码实现，巧用ZIP函数）：

def rotate1(self, matrix):
    matrix[:] = list(map(list,zip(*matrix[::-1])))

我们看看方法三做了什么？

[[1,2,3],
[4,5,6],
[7,8,9]]

先对矩阵进行了逆序：

test = [[1,2,3],
        [4,5,6],
        [7,8,9]]
print(test[::-1])
print(list(zip(*test[::-1])))  #解压之后内部为元组，所以使用map迭代式 list
print(list(map(list,zip(*test[::-1]))))