(在word里我都标了颜色。。。直接复制过来就没了 这里就不标了)
注意边的数量
初始化
不能放过每一个条件 考虑如何实现 (emm。。。因为这句话19年山东省赛那个水题。。我思考了很久边到底有啥用。。。)
图论多了解类型 这篇文章能解大部分吧。。 连通图的看lrj蓝书就好了
2——sat :
https://www.cnblogs.com/WTSRUVF/p/9791282.html
在这
其它的没写的 就多看看lrj蓝书
二分图:
普通匹配Dinic
带权二分图 KM
写之前一定要确定,我们要求什么,要用到什么。
染色法:
如果分为两队
使每队里的人都相互认识 则不认识的两个人建边然后染色
使每队里的人都不相互认识 则认识的两个人建边然后染色
二分图中不存在奇环, 所以可以用染色法判断奇环
把原图分成二分图且使子图的边数 >= m/2 则在染色一个的时候判断在这之前它和黑色、白色 哪个连的多,把它归为少的一方。
最大匹配:二分图中边集的数目最大的那个匹配;
最小顶点覆盖:用最少的点,让每条边都至少和其中一个点关联; = 最大匹配
最小边覆盖:用尽量少的不相交简单路径覆盖有向无环图(DAG)G的所有顶点; (本质就是求有向最长路径)= 顶点数 - 最大匹配
最大独立集:在N个点的图G中选出m个点,使这m个点两两之间没有边的点中,m的最大值。 = 顶点数 - 最大匹配
网络流:
看到棋盘模型先来一套黑白染色冷静一下!!!
用费用流实现控制次数的最短路
最小割:
满流的边即为要删除的边
最小割即为最小价值损失
对于指定要取的点,则它与源||汇点的边的权值为INF,表示不可满流,不可删除
对于有联系的点,两点边权为他们的关系权值
总权值加和 - Dinic() 即为答案
无向图最小割
预定义状态建边
归类建边
按时间点、时间段建边
费用流 拆容量控制流量 费用为差值
二分图多重最优匹配 Dinic
二分图多重最大匹配 费用最大流
有向环最小权覆盖
有向环最小权覆盖是一个哈密顿回路,有环, 求的是在环中的边的和的最小值 即Node[i].c == 0 的和的最小值 用KM或spfa
如果是无向图 记得w[i][j] = w[j][i] = min(w[i][j], tmp);
最小边集覆盖(点不相交 每个点只在一条路上)
最小边集覆盖是一个有向无环图,求的是n - max_flow, 即无环图的个数 用Dinic 或 匈牙利 hk
最大权闭合子图
有向图,每个点有点权,点权可正可负。对于任意一条有向边i和j,选择了点i就必须选择点j,你需要选择一些点使得得到权值最大。
盈利在左边 花费在右边
然后所有盈利 - 最大流 就是答案
输出方案:
如果左边的点i的d[i] != 0 则说明i被选择
如果右边的点j的d[j] != 0 则说明j被选择
最大密度子图
s 向每条边建权值为1的边
每条边向u和v建权值为INF的边
每个点向t建权值为mid的边
二分mid
while(r - l > (1.0 / n / n))
{
double mid = (r + l) / (double) 2;
build(mid);
if(sum - Dinic() > eps) l = mid;
else r = mid;
}
输出点集
void f_dfs(int u)
{
for(int i = head[u]; i != -1; i = nex[i])
{
int v = Node[i].v;
if(!vis[v] && Node[i].c > eps)
{
vis[v] = 1, f_dfs(v);
if(v - m >= 1 && v - m <= n) ans++;
}
}
}
然后 输出1 ~ n中被标记的点
s - t平面图最大流
(这个去参考一下那个国家队的论文。。。这个图就是那个的 看的时间太久远了忘了哪个了 百度吧。。。)
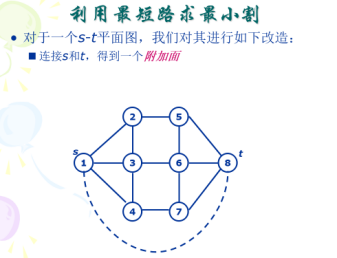

原s t之间连边
里面的为s* 外面的为t*
空地之间建边
跑spfa
连通图
1、建图 2、缩点 [3、统计度数]
遇到问是否u 能到 v啥的之类的 直接先一套连通图
因为任意两个在一个连通图中的点都可以相互到达
然后就算每个连通图之间都有边,那顶多就是一个有向无环图
点双连通分量
点不重复的路径、任意两条边都在同一个简单环中(无自环、无重边)、内部无割顶
边双连通分量
边不重复的路径、每条边都至少在一个简单环中、内部所有边都不是桥
强连通分量缩点 能求有向无环最长路
结合Dinic最小路径覆盖(点不相交) 求有几条
环是最基本的连通分量
在树中至少添加多少条边能使图变为双连通图。
结论:添加边数=(树中度为1的节点数+1)/2
最短路
数据量大两点之间的最短路
LCA + spfa
1、Lca的dfs时处理出所有的非树边的点 存起来(在dfs v的时候 如果v已经被遍历过了那么 u 和 v 都是非树边的点)
2、遍历所有非树边的点spfa求出到所有点的最短路dis[i][j] (第一维用非树边的点存在数组中的下标 (减少空间))
3、对于每次询问(设非树边的点存在int a[maxn]中,且有ans个)
int x = lca(u, v);
LL res = dep[u] + dep[v] - 2 * dep[x];
for(int i = 1; i <= ans; i++)
{
res = min(res, d[i][u] + d[i][v]);
}
printf(“%d ”, res);
1、普通最短路(双向 反向建边)
2、判断环路 (正环 负环)(dfs标记环路) (解法:spfa 在进队后判断if(++ans[e.v] > n ) return 1;)
3、层次网络 (解法:因为分层,所以把层抽象为一个点,然后把本层的各点与层连线, 然后层与层之间连线 )
4、差分约束 (spfa直接跑)
求最大值: 对于不等式 x[i] - x[j] <= a[k],对结点 j 和 i 建立一条 j -> i的有向边,求最短路
求最小值: 对于不等式x[i] - x[j] >= a[k],对结点 j 和 i 建立一条 j -> i的有向边,求最长路
如果图不连通,则在spfa开始时,把所有的结点放进队列,如下代码
无论求最大还是求最小 都这样写
for(int i=1; i<=n; i++)
{
Q.push(i);
d[i] = 0;
vis[i] = 1;
}
注意下界 其它最短路无源也这么写
注意隐含条件,一般都是相邻的两个点之间
i 和 i + 1
如果每个点都有个范围 则 设一个源点n + 1
以ZOJ 4028为例
l <= a[i] <= r
则 l <= a[i] - a[n - 1] <= r
存在负环的话是无解
求不出最短路
dist[ ]没有得到更新 (先判断是否有负环 再判断能否求出最短路 即是否为任意解 再输出正解
if(spfa())
printf("无解 ");
else if(d[n] == INF)
printf("任意解 ");
else
printf("%d ", d[n]);
做差分约束一定要找个不等式关系,一般都有两个未知变量,像hdu1384 求的是与这个区间重合的元素,那我们就可以转化为sum(a)表示0到a区间与答案集合重合的元素
然后sum(b) - sum(a - 1) >= w 或者 <= w 是不是就可以了 sum(a) 和 sum(b) 分别用a 和 b来表示就可以了
像hdu 3666 有乘积的不等式 一定要想到log一下那么log(a) 和 log(b) 就可以分别用行和列来表示
6、传递闭包(传递一种关系 用Floyd)
7、最大值最小化
if(d[e.v] > max(d[x],e.d))
{
d[e.v] = max(d[x],e.d);
if(!vis[e.v])
{
Q.push(e.v);
vis[e.v] = 1;
}
}
最小值最大化
if(d[e.v] < min(d[x],e.d))
{
d[e.v] = min(d[x],e.d);
if(!vis[e.v])
{
Q.push(e.v);
vis[e.v] = 1;
}
}
8、分层最短路(dijkstra)
最小生成树
步骤:
先用Node存边
按权值从小到大排序(如果有输出按字典序 则如果权值相等按u排,u还相等按v排)
选取每条边并查集
同时res += Node[i].w;
多次询问两点间最短路的最大值最小化 最小瓶颈生成树